Descomposición de una fracción racional en fracciones simples
Cuando el denominador de una fracción algebráica puede descomponerse en factores, la fracción se puede escribir como suma o diferencia de otras fracciones más sencillas.
Este proceso se conoce como descomposición en fracciones simples.
1) El denominador es un polinomio de segundo grado con dos raíces reales simples
ax2 + bx + c = 0
Tiene dos raíces reales distintas x = x1 y x = x2
La descomposición es la siguiente:
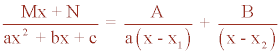
Los valores A y B se determinan por el método de identificación de coeficientes.
Ejemplo de descomposición en fracciones simples:
![]()
Como las soluciones de x2 - 5x + 6 = 0 son x1 = 3 y x2 = 2 , la descomposición que se hace es la siguiente:
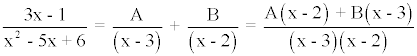
La fracción dada y la obtenida al sumar las dos fracciones simples son iguales. Como sus denominadores son iguales, también deben serlo sus numeradores. Por lo tanto:
3x - 1 = A(x - 2) + B(x - 3)
Para x = 2 tenemos que: 6 - 1 = - B ⇒ B = - 5
Para x = 3 tenemos que: 9 - 1 = A ⇒ A = 8
Por lo tanto la descomposición queda de la siguiente manera:
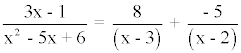
Otra forma de realizar la descomposición es a partir de la identificación de coeficientes
3x - 1 = A(x - 2) + B(x - 3)
3x - 1 = Ax - 2A + Bx - 3B
3x - 1 = (A + B)x - (2A + 3B)
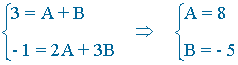
2) El denominador es un polinomio de segundo grado con una raíz real doble
ax2 + bx + c = 0
Tiene una raíz real doble x = x1
La descomposición es la siguiente:
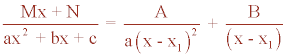
3) El denominador tiene factores lineales de la forma x - a
Q(x) = (x - a1) · (x - a2) · (x - a3) · ... · (x - an)
Tiene n raíces reales x = a1 , x = a2 , x = a3 ... x = an
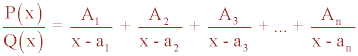
4) El denominador es un polinomio de la forma (ax + b)n
Q(x) = (ax + b)n
Tiene n raíces iguales x = - b/a
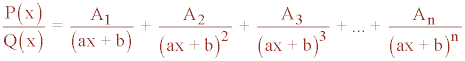
5) El denominador tiene un factor cuadrático irreducible de la forma ax2 + bx + c
Q(x) = ax2 + bx + c irreducible, es decir, no se puede descomponer en dos factores lineales, ya que las raíces son imaginarias.
Por tanto b2 - 4ac < 0 , siendo a , b y c números reales donde a ≠ 0
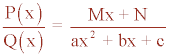
6) El denominador es un polinomio de la forma (ax2 + bx + c)n
Q(x) = (ax2 + bx + c)n donde ax2 + bx + c es irreducible, es decir, no se puede descomponer en factores lineales
Por tanto b2 - 4ac < 0 , siendo a , b y c números reales donde a ≠ 0
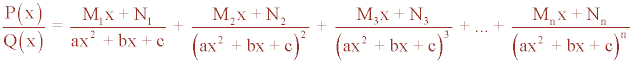


 INICIO
INICIO
