Ejercicios resueltos de descomposición de una fracción racional en fracciones simples
Descomponer en fracciones simples:
![]()
Primero factorizamos el denominador:
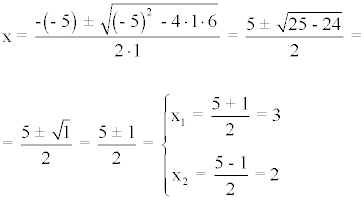
Es decir, el denominador se factoriza de la siguiente manera:
x2 - 5x + 6 = (x - 3) (x - 2)
Aplicando la fórmula de la descomposición, tenemos que:
![]()
Desarrollando el segundo término de la ecuación obtenemos que:
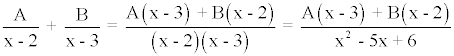
Igualando numeradores tenemos que:
x = A(x - 3) + B(x - 2)
Resolvemos sustituyendo x por los valores que anulen los denominadores de las fracciones:
Para x = 3 tenemos que: 3 = B
Para x = 2 tenemos que: 2 = - A
Por lo tanto la solución es:
![]()
También se puede utilizar el método de identificación de coeficientes de igual potencia:
x = A(x - 3) + B(x - 2)
x = Ax - 3A + Bx - 2B
x = (A + B)x + (- 3A - 2B)
Los valores A y B se determinan por el método de identificación de coeficientes:
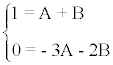
Multiplicamos la primera ecuación por 3 y utilizamos el método de reducción:
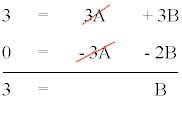
Por lo tanto tenemos que:
B = 3
Sustituyendo en la primera ecuación del sistema:
1 = A + 3 ⇒ A = - 2
Descomponer en fracciones simples:
![]()
Primero factorizamos el denominador:
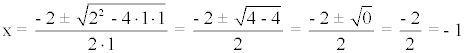
Es decir, el denominador tiene una raíz real doble, por tanto la descomposición es de la forma:
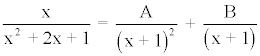
Desarrollando el segundo término de la ecuación obtenemos que:
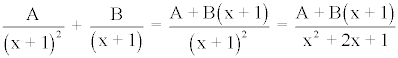
Igualando numeradores tenemos que:
x = A + B(x + 1)
Resolvemos sustituyendo x por el valor que anula a los denominadores de las fracciones y usando un valor arbitrario para x :
Para x = - 1 tenemos que: - 1 = A
Para x = 0 tenemos que: 0 = - 1+ B ⇒ B = 1
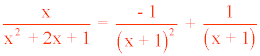
También se puede utilizar el método de identificación de coeficientes de igual potencia:
x = A + B(x + 1)
x = A + Bx + B
x = Bx + (A + B)
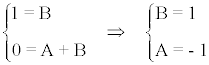
Descomponer en fracciones simples:
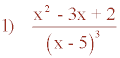
El denominador posee una raíz real triple, por lo tanto:
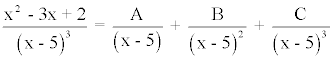
Desarrollando el segundo término obtenemos que:
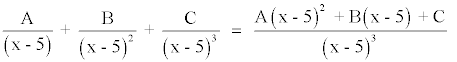
Igualando los numeradores tenemos que:
x2 - 3x + 2 = A(x - 5)2 + B(x - 5) + C
Resolvemos sustituyendo x por el valor que anula al denominador y usando valores arbitrarios para x :
Para x = 5 tenemos que:
25 - 15 + 2 = C
C = 12
Para x = 0 tenemos que:
2 = 25A - 5B + 12
Para x = 1 tenemos que:
1 - 3 + 2 = 16A - 4B + 12 ⇒ 0 = 16A - 4B + 12
Por lo tanto tenemos el siguiente sistema:
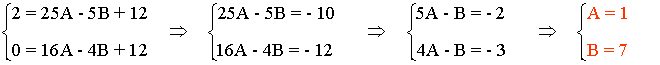
Por tanto la solución es:
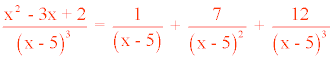
También se puede utilizar el método de identificación de coeficientes de igual potencia:
Para x = 5 tenemos que:
25 - 15 + 2 = C
Sustituyendo el valor de C obtenemos:
x2 - 3x + 2 = A(x - 5)2 + B(x - 5) + 12
x2 - 3x + 2 = A(x2 - 10x + 25) + B(x - 5) + 12
x2 - 3x + 2 = Ax2 - 10Ax + 25A + Bx - 5B + 12
x2 - 3x + 2 = Ax2 - (10A - B)x + (25A - 5B + 12)
Los valores A y B se determinan por el método de identificación de coeficientes:
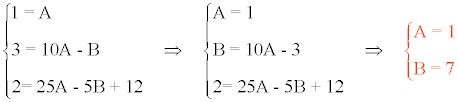
Descomponer en fracciones simples:
![]()
Descomponemos en factores el denominador:
Aplicamos la regla de Ruffini sabiendo que el valor 1 anula al denominador:
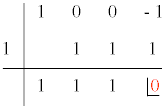
Es decir, el denominador se descompone de la siguiente forma:
x3 - 1 = (x - 1) (x2 + x + 1)
Por lo tanto podemos tenemos que:
![]()
Desarrollando el segundo término obtenemos que:
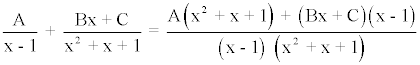
Igualando los numeradores tenemos que:
3x - 5 = A(x2 + x + 1) + (Bx + C)(x - 1)
Para x = 1 tenemos que:
- 2 = A(1 + 1 + 1) ⇒ - 2 = 3A
A = - 2/3
Utilizamos el valor de A en la ecuación anterior y simplificamos:
![]()
Quitando denominadores tenemos que:
3(3x - 5) = - 2(x2 + x + 1) + 3(Bx + C)(x - 1)
9x - 15 = - 2x2 - 2x - 2 + 3(Bx + C)(x - 1)
2x2 + 11x - 13 = 3(Bx + C)(x - 1)
2x2 + 11x - 13 = 3Bx2 - 3Bx + 3Cx - 3C
2x2 + 11x - 13 = 3Bx2 + (3B - 3C)x - 3C
Los valores B y C se determinan por el método de identificación de coeficientes:
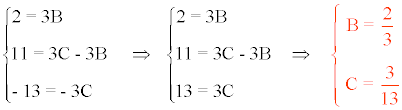
Por lo tanto tenemos que:
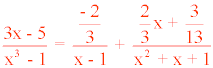
Descomponer en fracciones simples:
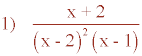
El denominador posee una raíz real doble x = 2 y una raíz real simple x = 1 , por lo tanto se descompone de la siguiente manera:
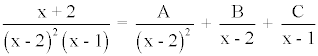
Desarrollando el segundo término tenemos que:
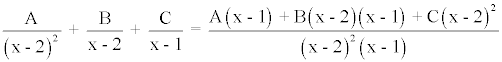
Igualando numeradores obtenemos lo siguiente:
x + 2 = A(x - 1) + B(x - 2)(x - 1) + C(x - 2)2
Para x = 1 tenemos que:
3 = C·(- 1)2
C = 3
Para x = 2 tenemos que:
4 = A·1
A = 4
Por lo tanto, sustituyendo los valores de A y C obtenemos:
x + 2 = 4(x - 1) + B(x - 2)(x - 1) + 3(x - 2)2
x + 2 = 4x - 4 + B(x2 - x - 2x + 2) + 3(x2 - 4x + 4)
x + 2 = 4x - 4 + Bx2 - 3Bx + 2B + 3x2 - 12x + 12
x + 2 = Bx2 + 3x2 - 3Bx - 8x + 2B + 8
x + 2 = (B + 3)x2 + (- 3B - 8)x + (2B + 8)
El valor de C se determina por el método de identificación de coeficientes:
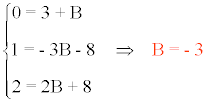
Por tanto la solución es:
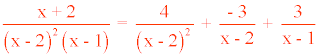
Descomponer en fracciones simples:
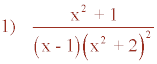
El denominador tiene una raíz real simple y dos raíces no reales.
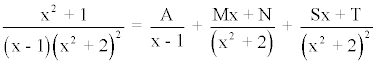
Desarrollando el segundo término tenemos que:

Igualando numeradores obtenemos lo siguiente:
x2 + 1 = A(x2 + 2)2 + (Mx + N)(x - 1)(x2 + 2) + (Sx + T)(x - 1)
x2 + 1 = A(x4 + 4x2 + 4) + (Mx + N)(x3 + 2x - x2 - 2) + (Sx + T)(x - 1)
x2 + 1 = Ax4 + 4Ax2 + 4A + Mx4 + 2Mx2 - Mx3 - 2Mx + Nx3 + 2Nx - Nx2 - 2N + Sx2 - Sx + Tx - T
x2 + 1 = (A + M)x4 + (N - M)x3 + (4A + 2M - N + S)x2 + (- 2M + 2N - S + T)x + (4A - 2N - T)
Los valores de A , M , N , S y T se determinan por el método de identificación de coeficientes:
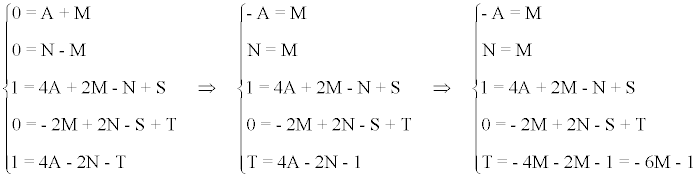
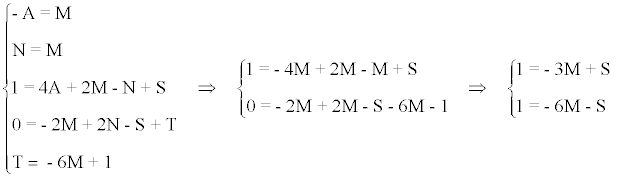
Aplicando el método de reducción tenemos que:
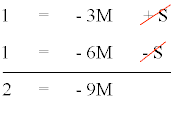
Por lo tanto obtenemos que:
M = - 2/9 N = - 2/9 A = 2/9 S = 1/3 T = 1/3
Es decir, la solución es:
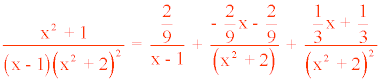


 INICIO
INICIO