Binomio de Newton
Números combinatorios
Dado un número natural m, llamamos factorial de m, y lo denotamos por m! , al producto de m por todos los números naturales menores que él.
m! = m · (m - 1) · (m - 2) · ... · 3 · 2 · 1
Dados dos números naturales m y n, tales que n≤m, definimos el número combinatorio "m sobre n" como:
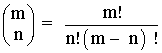
0! = 1
1! = 1
Propiedades de los números combinatorios
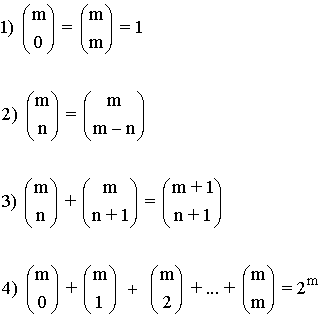
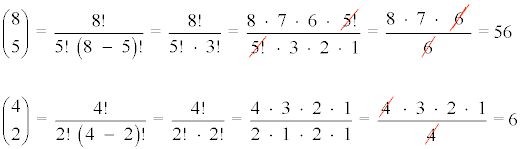
Ejemplos de números combinatorios
Binomio de Newton
La fórmula del binomio de Newton sirve para calcular las potencias de un binomio utilizando números combinatorios.
Desarrollo de (a + b)m
![]()
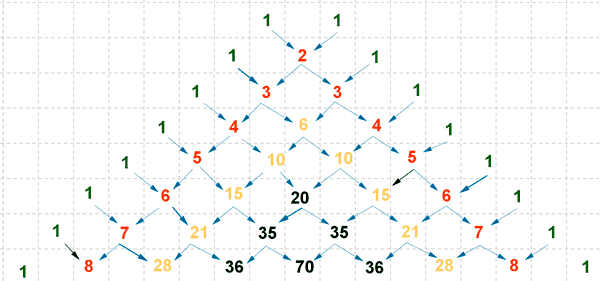
Triangulo de Tartaglia o triángulo de Pascal
Para hallar los coeficientes del binomio de Newton nos podemos ayudar del triángulo de Tartaglia o triángulo de Pascal:
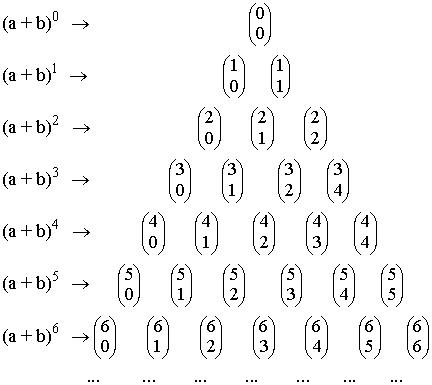
Ejemplo de binomio de Newton:
Obtén el polinomio que resulta de desarrollar la expresión (2 + 3x3)4.
Aplicamos la fórmula del binomio de Newton (a + b)n.
Donde a = 2 , b = 3x3 y n =4
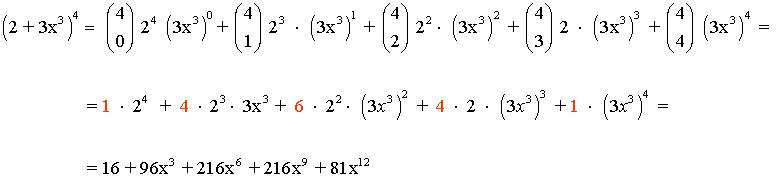
Donde los coeficientes marcados en rojo corresponden con los del triángulo de Tartaglia o triángulo de Pascal.
1) (x - 3)5
Aplicamos la fórmula del binomio de Newton (a + b)n.
Donde a = x , b = -3 y n =5
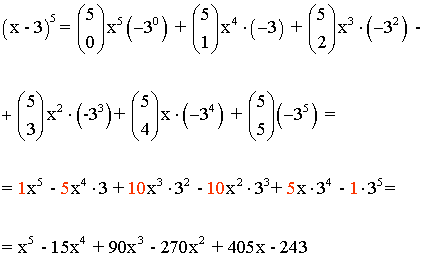
Donde los coeficientes marcados en rojo corresponden con los del triángulo de Tartaglia o triángulo de Pascal.
Término general
El término general es el que ocupa el lugar n + 1.
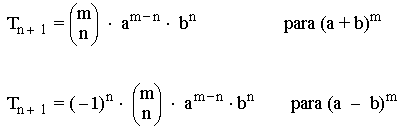
Ejemplo de término general:
Hallar el octavo término del desarrollo de (3x + 2y)15
Calculamos el término octavo utilizando la fórmula para a = 3x , b = 2y , n = 7 m =15
![]()
El desarrollo del número 15 sobre 7 es el siguiente:
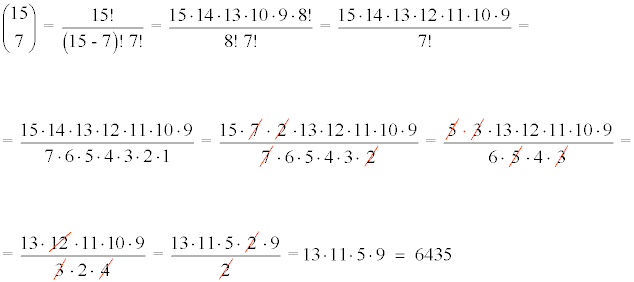
Por lo tanto el octavo término se expresa de la siguiente manera:
![]()


 INICIO
INICIO

