Ejercicios resueltos del binomio de Newton
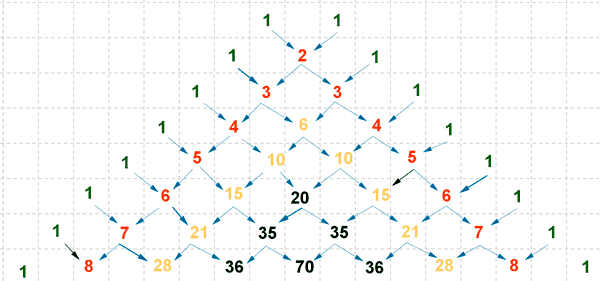
Fórmulas y triángulo de Tartaglia o triángulo de Pascal
![]()
![]()
![]()
Desarrollar aplicando el binomio de Newton:
1) (x - 3)5
Aplicamos la fórmula del binomio de Newton (a + b)n.
Donde a = x , b = -3 y n =5
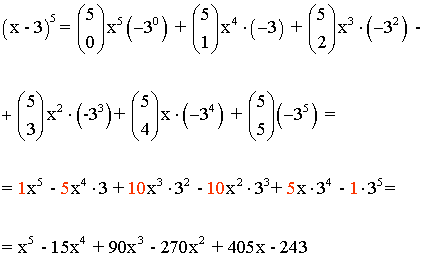
2) (3x - 2y)6
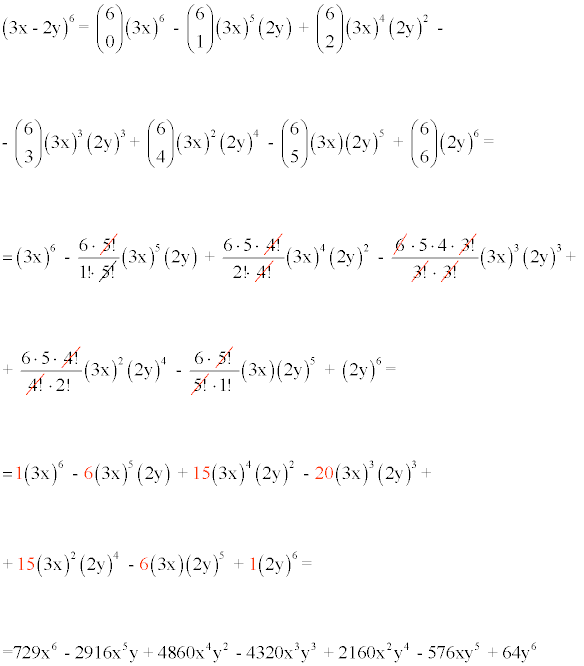
Desarrollar aplicando el binomio de Newton:
1) ( - 1 - 3x)9
Aplicamos la fórmula del binomio de Newton (a + b)n.
Donde a = - 1 , b = - 3x y n = 9.
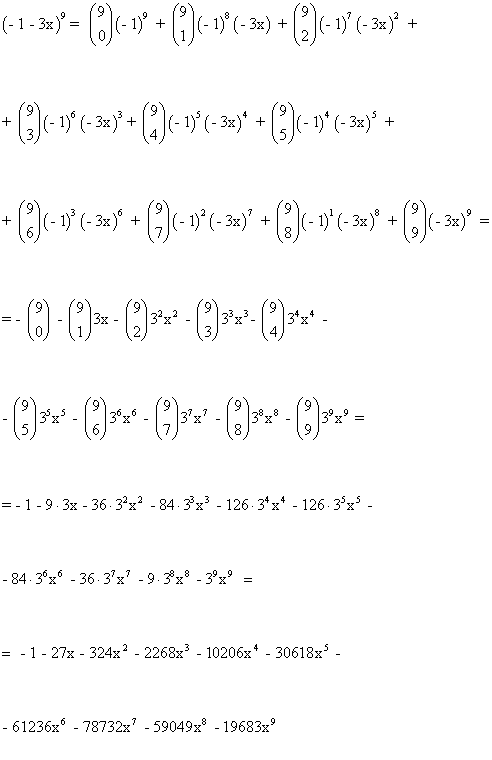
Los cálculos de los coeficientes de los anteriores números combinatorios son los siguientes:
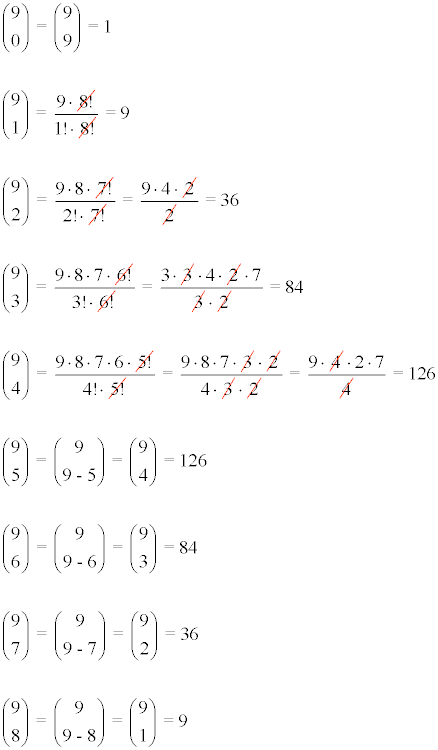
Desarrollar aplicando el binomio de Newton:
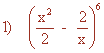
Aplicamos la fórmula del binomio de Newton (a + b)n.
Donde a = x2/2 , b = -2/x y n = 6.
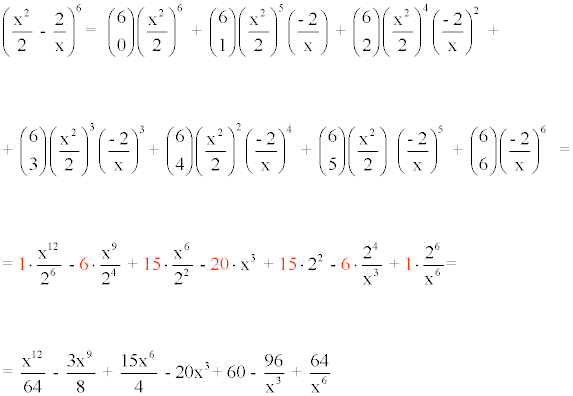
Desarrollar aplicando el binomio de Newton:
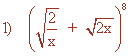
Aplicamos la fórmula del binomio de Newton (a + b)n.
![]()
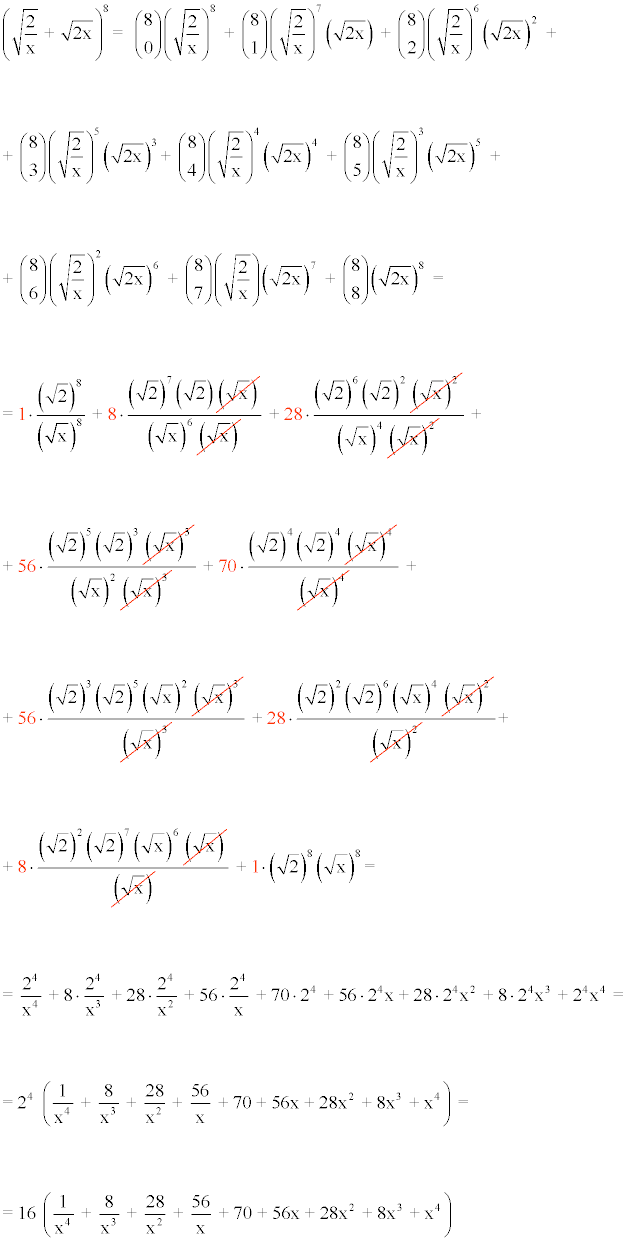
Los cálculos de los coeficientes de los anteriores números combinatorios son los siguientes:
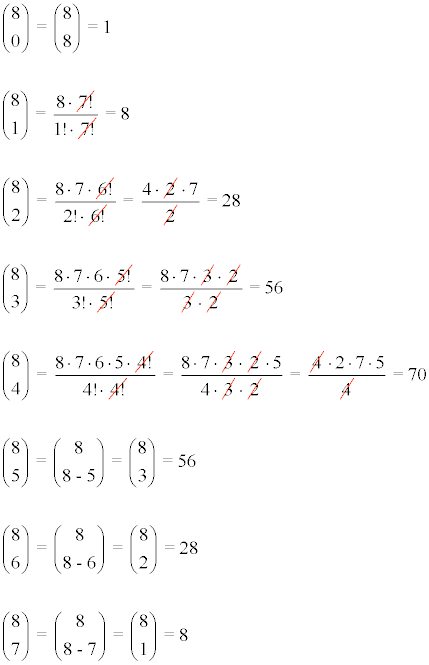
Hallar un término del desarrollo del binomio de Newton:
1) Hallar el término quinto del desarrollo de (1 + y)12
Recordemos la fórmula para calcular el término general del binomio de Newton:
![]()
Calculamos el término quinto utilizando la fórmula para a = 1 , b = y , n = 4.
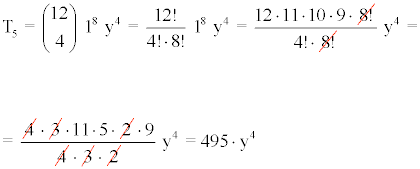
2) Hallar el término séptimo del desarrollo de (2 + 3x)9
Calculamos el término séptimo utilizando la fórmula para a = 2 , b = 3x , n = 6.
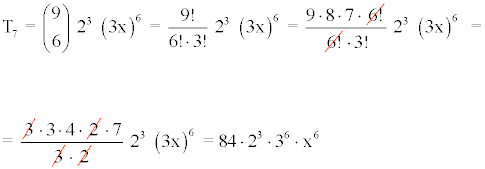
3) Hallar el término octavo del desarrollo (2x - y)10
Calculamos el término octavo utilizando la fórmula para a = 2x , b = - y , n = 7.
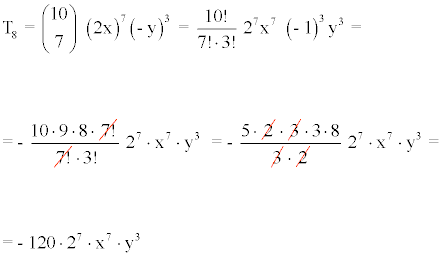
Hallar el término medio de los desarrollos siguientes:
1) (x + y)10
El desarrollo anterior posee 11 términos (m = 10).
Por lo tanto, el término medio coincide con el término sexto.
Es decir, hallamos el término sexto para a = x , b = y , n = 5.
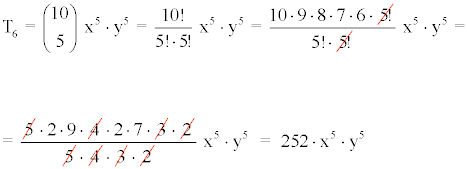
![]()
El desarrollo anterior posee 17 términos (m = 16).
Por lo tanto, el término medio coincide con el término noveno.
Es decir, hallamos el término sexto para a = 2x , b = -1/2x , n = 8.
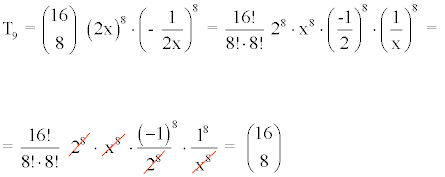
1) Hallar el término que contiene a la potencia x6 en el desarrollo de (2x + 5)15.
![]()
Por lo tanto, n = 9 , es decir, buscamos el término décimo:
![]()
![]()
El término general del desarrollo es:
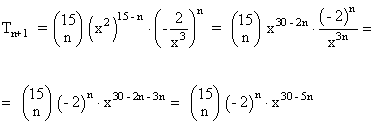
Para hallar el término de grado 5, se tiene que cumplir que:
30 - 5n = 5
Por lo tanto n = 5 y el término es:
![]()
Por otra parte, para calcular el término independiente se tiene que cumplir que:
30 - 5n = 0
Es decir, n = 6 y el término es:
![]()
3) Calcular el término en el que el exponente de a y el exponente de b son iguales en el desarrollo de (a - b2)15
El término general del desarrollo es el siguiente:
![]()
Para que el exponente de los términos a y b sean iguales, se tiene que cumplir que:
15 - n = 2n
Es decir, n = 5
Por lo tanto el término que buscamos es:
![]()
Cuadrados y cubos de un polinomio:
1) (2a - 3b + 4c)2
Aplicamos la propiedad asociativa.
(2a - 3b + 4c)2 = [(2a - 3b) + 4c]2 = (2a - 3b)2 + 2(2a - 3b)4c + (4c)2 = (2a)2 - 2(2a)(3b) + (3b)2 + 16ac - 24bc + (4c)2 = 4a2 - 12ab + 9b2 + 16ac - 24bc + 16c2 = 4a2 + 9b2 + 16c2 - 12ab + 16ac - 24bc
O aplicamos la fórmula: (a + b + c)2 = a2 + b2 + c2 + 2ab + 2ac + 2bc
(2a - 3b + 4c)2 = (2a)2 + (-3b)2 + (4c)2 + 2(2a)(-3b) + 2(2a)(4c) + 2(-3b)(4c) = 4a2 + 9b2 + 16c2 - 12ab + 16ac - 24bc
![]()
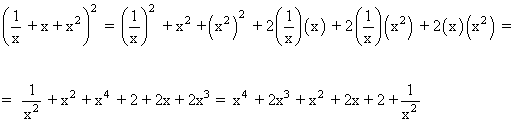
3) (2 + 3x - 5x2)3
(2 + 3x - 5x2)3 = (2 + 3x - 5x2) (2 + 3x - 5x2)2 = (2 + 3x - 5x2) (4 + 9x2 + 25x4 + 12x - 20x2 - 30x3) = (2 + 3x - 5x2) (25x4 - 30x3 - 11x2 + 12x + 4) = -125x6 + 225x5 + 15x4 - 153x3 - 6x2 + 36x + 8
4) (1 + x + x2 + x3)3
(1 + x + x2 + x3)3 = [(1 + x) + (x2 + x3)]3 = (1 + x)3 + 3(1 + x)2(x2 + x3) + 3(1 + x)(x2 + x3)2 + (x2 + x3)3 = 1 + 3x + 3x2 + x3 + 3x2 + 3x3 + 3x4 + 3x5 + 3x7 + 9x6 + 9x5 + 3x4 + x6 + 3x7 + 3x8 + x9 = x9 + 3x8 + 6x7 + 10x6 + 12x5 + 6x4 + 4x3 + 6x2 + 3x + 1


 INICIO
INICIO