Dominio y recorrido de las funciones trigonométricas
Las funciones f(x) = sen g(x) y f(x) = cos g(x) están definidas siempre que lo esté la función g(x) .
La función f(x) = tg g(x) está definida siempre que g(x) ≠ π/2 + k·π
| Dominio | Imagen, rango o recorrido | |
|---|---|---|
| y = sen x | R |
{ y∈R | -1 ≤ y ≤ 1 } |
| y = cos x | R |
{ y∈R | -1 ≤ y ≤ 1 } |
| y = tg x | { x∈R | x ≠ π/2 (2k + 1) } |
R |
| y = cotg x | { x∈R | x ≠k·π } |
R |
| y = sec x | { x∈R | x ≠ π/2 (2k + 1) } |
{ y∈R | y ≤ -1 ó y ≥ 1 } |
| y = cosec x | { x∈R | x ≠k·π } |
{ y∈R | y ≤ -1 ó y ≥ 1 } |
Ejemplos de dominio de funciones trigonométricas
![]()
El dominio de f(x) es R . Dom(f) = R .
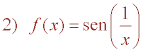
La función f(x) no está definida cuando x = 0 . Dom(f) = R - {0} .
![]()
La función f(x) no está definida cuando x > 1 . Dom(f) = (- ∞, 1] .
![]()
La función f(x) no está definida cuando:
![]()
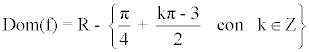
Dominio y recorrido de las funciones trigonométricas inversas
| Dominio | Imagen, rango o recorrido | |
|---|---|---|
| y = arc sen x | { x ∈ R | - 1 ≤ x ≤ 1 } |
{ y ∈ R | - π/2 ≤ y ≤ π/2 } |
| y = arc cos x | { x ∈ R | - 1 ≤ x ≤ 1 } |
{ y ∈ R | 0 ≤ y ≤ π } |
| y = arc tg x | R |
{ y ∈ R | - π/2 ≤ y ≤ π/2 } |
| y = arc cotg x | R |
{ y ∈ R | 0 ≤ y ≤ π } |
| y = arc sec x | { x ∈ R | x ≤ - 1 ó x ≥ 1 } |
{ y ∈ R | 0 ≤ y ≤ π , y ≠ π/2 } |
| y = arc cosec x | { x ∈ R | x ≤ - 1 ó x ≥ 1 } |
{ y ∈ R | - π/2 ≤ y ≤ π/2 , y ≠0 } |


 INICIO
INICIO

