Funciones logarítmicas
Las funciones logarítmicas son funciones del tipo:
![]()
Es la inversa de la función exponencial f(x) = ax
Las características generales de las funciones logarítmicas son:
1) El dominio de una función logarítmica son los números reales positivos: Dom(f) = (0. + ∞) .
2) Su recorrido es R: Im(f) = R .
3) Son funciones continuas.
4) Como loga1 = 0 , la función siempre pasa por el punto (1, 0) .
La función corta el eje X en el punto (1, 0) y no corta el eje Y.
5) Como logaa = 1 , la función siempre pasa por el punto (a, 1) .
6) Si a > 1 la función es creciente.
Si 0 < a < 1 la función es decreciente.
7) Son convexas si a > 1 .
Son concavas si 0 < a < 1 .
8) El eje Y es una asíntota vertical.
- Si a > 1 :
Cuando x → 0 + , entonces log a x → - ∞ - Si 0 < a < 1 :
Cuando x → 0 + , entonces log a x → + ∞
Ejemplo de funciones logarítmicas:
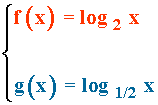
1) Dominio:
El dominio de las funciones logarítmicas es (0, + ∞) .
Dom(f) = Dom(g) = (0, + ∞) .
2) Recorrido:
El recorrido de las funciones logarítmicas es R.
Im(f) = Im(g) = R .
3) Puntos de corte:
f(1) = log21 = 0 , el punto de corte con el eje X es (1, 0).
g(1) = log1/21 = 0 , el punto de corte con el eje X es (1, 0).
La funciones f(x) y g(x) no cortan al eje Y.
3) Crecimiento y decrecimiento:
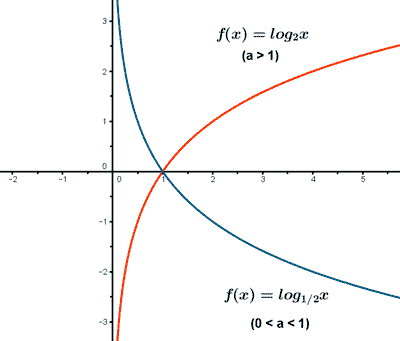
La función f(x) es creciente ya que a > 1 .
La función g(x) es decreciente ya que 0 < a < 1 .
4) Concavidad y convexidad:
Las función f(x) es convexa ya que a > 1 .
Las función g(x) es concava ya que 0 < a < 1 .
5) Asíntotas:
Las funciones f(x) y g(x) tienen una asintota en el eje Y.
6) Tabla de valores:
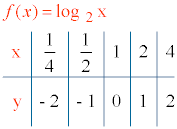
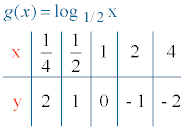
Resumen de las propiedades de la función logaritmo neperiano
| 1 | La función logarítmica es la inversa de la exponencial: y = Ln x ⇔ x = ey |
|---|---|
| 2 | La función y = Ln x tiene por dominio { x ∈ R | x > 0 } y por recorrido R . |
| 3 | La función y = Ln x es continua, creciente e inyectiva en todo su dominio. |
| 4 | La función y = Ln x es convexa o cóncava hacia abajo en todo su dominio. |
| 5 | 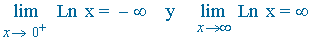 |
La función logarítmo neperiano: f(x) = ln x
La función logarítmo neperiano es la inversa de y = ex .
Su gráfica es simétrica de y = ex respecto a y = x .
y = ex
x = ey
Por definición: y = ln x
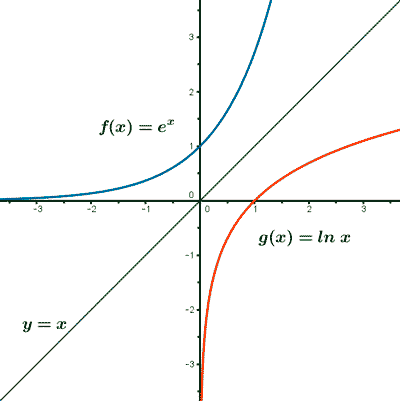


 INICIO
INICIO

