Construcción de figuras semejantes.
Dos figuras están en posición de Tales si tienen un ángulo común y todos los lados homólogos que pasan por el vértice común son paralelos. Dos vértices homólogos siempre están alineados con el vértice común.
![]()
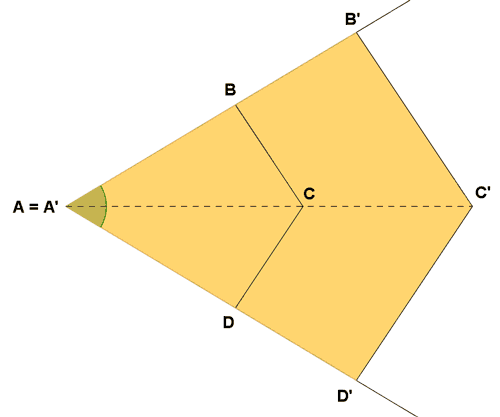
Si dos figuras están en posición de Tales, entonces son semejantes, ya que:
• Los ángulos correspondientes son iguales, pues uno de ellos es común y los otros tienen lados paralelos
• Los lados correspondientes son proporcionales, pues según el teorema de Tales:
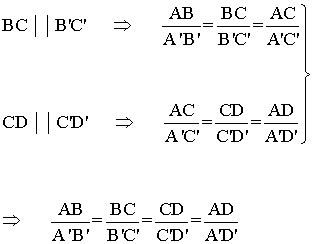
Dos polígonos son semejantes si tienen sus ángulos iguales y los lados proporcionales.
Ejemplo 1 :
Construye una figura semejante a este con razón de semejanza 2.
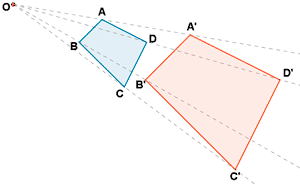
Desde un punto cualquiera O trazamos rectas que pasan por los vértices de la figura.
En cada una de esas rectas marcamos los puntos A', B', C' y D' de forma que :
OA' = 2 · OA ; OB' = 2 · OB ; OC' = 2 · OC ; OD' = 2 · OD
La figura es semejante a la figura ABCD con razón de semejanza 2.
Ejemplo 2 :
Construye una figura semejante a esta con razón de semejanza 0,5.
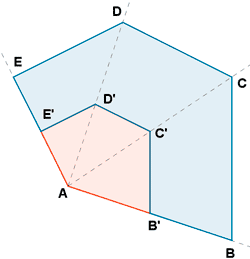
También podemos tomar como punto O uno de los vértices de la figura.
Procedemos de la misma manera que en el caso anterior. Trazamos rectas desde cada uno de los vértices y aplicamos la siguiente condición :
OB' = 0,5 · OB ; OC' = 0,5 · OC ; OD' = 0,5 · OD ; OE' = 0,5 · OE
La figura es semejante a la figura ABCDE con razón de semejanza 0,5.


 INICIO
INICIO

