Triángulos en posición de Tales.
Dos triángulos están en posición de Tales si tienen un ángulo común y los lados opuestos a este ángulo son paralelos.
Los triángulos en posición de Tales son semejantes.
Propiedades de dos triángulos en posición de Tales.
Tienen los lados proporcionales.
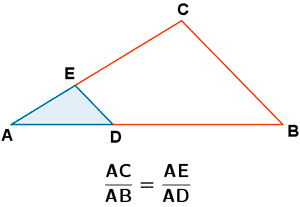
Tienen los ángulos iguales.
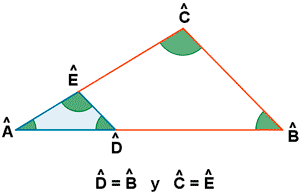
Dado un triángulo, para construir otro semejante, basta con trazar una recta paralela a uno de los lados.
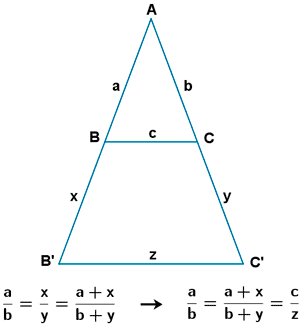
El triángulo ABC y el triangulo AB'C' son semejantes.
Ejemplo 1 :
Calcula la longitud de los segmentos cuyo valor es desconocido :

Los dos triángulos están en posición de Tales por lo que son semejantes.
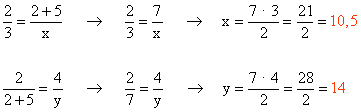
Ejemplo 2 :
En la siguiente figura, calcula la longitud desconocida :
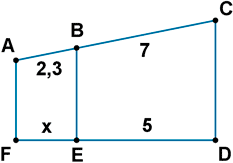
Si prolongamos los segmentos AC y FD estos se cortan, por lo que al ser secantes forman un triángulo y podemos aplicar el Teorema de Tales.
![]()
Ejemplo 3 :
Halla las longitudes x e y sabiendo que el perímetro del triángulo mayor mide 67 cm.
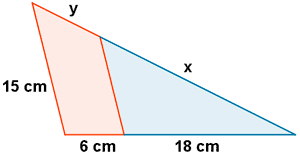
Los dos triángulos están en posición e Tales, ya que tienen un ángulo en común y los lados opuestos a él son paralelos. Teniendo en cuenta además que su perímetro es 67 cm, podemos plantear el siguiente sistema de ecuaciones :
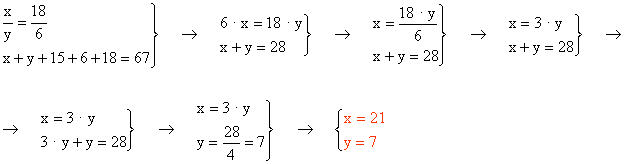


 INICIO
INICIO

