Rectas secantes cortadas por paralelas.
Secantes cortadas en segmentos iguales.
Observa la siguiente figura :
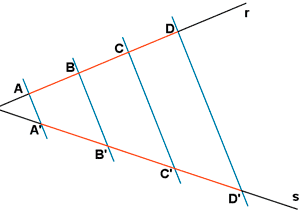
- r y s son dos rectas sec antes.
- Cuatro rectas paralelas costan r y s.
- Las cuatro rectas paralelas determinan tres segmentos iguales sobre r : AB = BC = CD
Demostraremos a continuación que los segmentos A'B', B'C' y C'D' sobre la recta s son también iguales.
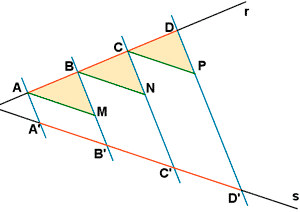
Trazamos segmentos paralelos a s desde los puntos A, B y C como se muestra en la figura.
Si ahora consideramos los triángulos AMB, BNC y CPD, podemos ver :
- Tienen un lado igual AB = BC = CD.
- Los cuatro ángulos son iguales, ya que son ángulos agudos de lados paralelos.
Así, los tres triángulos son iguales, y se cumple que AM = BN = CP
Además, por paralelismo se cumple AM = A'B' ; BN = B'C' ; CP = C'D'
Los tres segmentos determinados sobre la recta s por las rectas paralelas son iguales.
Si un conjunto de rectas paralelas corta a dos rectas secantes de forma que los segmentos determinados por ella son iguales, los segmentos correspondientes determinadas en la otra son iguales.


 INICIO
INICIO

