Problemas resueltos de medidas de ángulos.
1) Pasa a forma compleja los siguientes ángulos expresados en segundos :
a) 6 930 " b) 262 135 " c) 6 342 '
d) 32,5º e) 43,28º f) 21,7 '
2) Pasar a segundos los siguientes ángulos expresados en forma compleja :
a) 75º 25' 45" b) 33º 58' 4"
3) Utilizando la forma decimal expresa :
a) En grados : 55º 42' 30'' b) En grados : 120º 15' 40''
c) En minutos : 90º 37' 6'' d) En minutos : 35º 55' 17''
4)
5) Efectúa las siguientes operaciones con ángulos :
a) 24º 35' 19" + 16º 13' 31" b) 14º 28' 45" + 30º 34' 26"
c) 27º 36' 12" + 41º 39' 55" d) 47º 39' 52" - 17º 26' 20"
e) 38º 6' 18" - 11º 32' 51" f) 90º - 19º 52' 23"
g) 180º - 147º 31' 9" h) 270º - 100º 16' 38"
6) Efectúa las siguientes operaciones con ángulos :
a) ( 14º 8' 11" ) · 3 b) ( 21º 28' 17" ) · 5
c) ( 32º 30' 15") · 4 d) ( 145º 35' 52" ) : 5
e) ( 36º 47' 25" ) : 5 f) ( 145º 35' 48" ) : 12
7) Halla el doble, el triple y el cuadruple del ángulo 43º 17' 55"
8) En el ángulo
= 75º 41' 30" trazamos su bisectriz. ¿Cuánto mide cada ángulo restante?
9) Obtén en ángulo complementario y suplementario de los siguientes ángulos :
a) 35º b) 20º c) 59º 23' d) 17º 39' 45"
10) Dados los ángulos
= 48º 31' 27" y
= 25º 11' 15" determina el valor de de las amplitudes de estos ángulos :
a)+
b)
-
c) 2 ·
d) El complementario de+
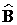
e) El suplementario de-
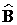
f) El suplementario de 2 ·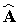
11) Dos ángulos son suplementarios y uno vale el doble que el otro. Halla el valor de dichos ángulos.
12) Dos ángulos son complementario y uno vale el cuádruple del otro. Halla el valor de dichos ángulos.
13) Determina la medida de estos dos ángulos, y resuelve las operaciones que se indican :
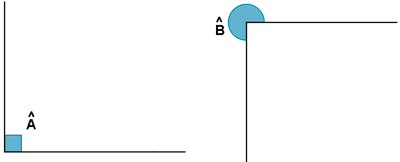
a)b)
c)
d)
14) Calcula la amplitud del ángulo X en cada figura :
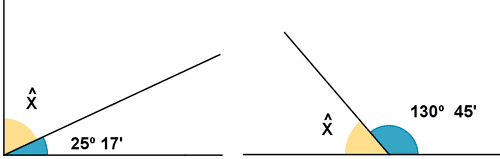
15) Calcula el valor exacto de los ángulos que forman la aguja horaria y el minutero de un reloj a las horas siguientes :
a) A las 4 de la mañana.
b) A las 4 y cuarto.
c) A las 4 y media.
d) A las 2 y 20 minutos.
1) Pasa a forma compleja los siguientes ángulos expresados en segundos :
a) 6 930 " b) 262 135 " c) 6 342 '
d) 32,5º e) 43,28º f) 21,7 '
a)
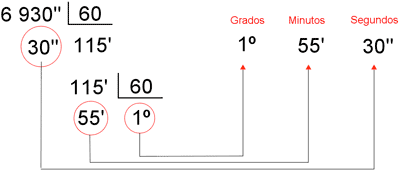
6 930 " = 1º 55' 30"
b)
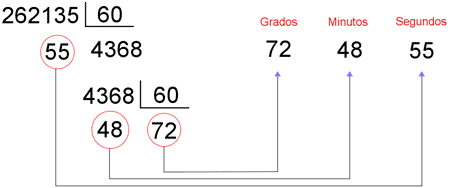
262 135" = 72º 48' 55"
c)
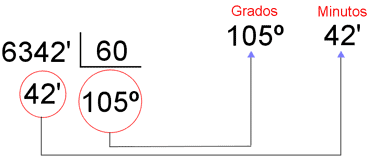
6 342' = 105º 42'
d)
En este caso, al ser números decimales, pasaremos la parte decimal a minutos.
32,5º → 0,5 · 60 = 30' → 32,5º = 32º 30'
e)
De forma análoga al apartado d, pasamos la parte decimal a minutos.
43,28º → 0,28 · 60 = 16,8' → Pasamos ahora la parte decimal de los minutos a segundos → 0,8 · 60 = 48" → 43,28º = 43º 16' 48"
f)
21,7' → 0,7 · 60 = 42" → 21,7' = 21' 42"
2) Pasar a segundos los siguientes ángulos expresados en forma compleja :
a) 75º 25' 45" b) 33º 58' 4"
a)
75º 25' 45" → 75 · 3600 + 25 · 60 + 45 =
270000 + 1500 + 45 = 271 545"
b)
En primer lugar pasamos los grados y minutos a segundos :
![]()
A continuación, sumamos todos los segundos :
118 800" + 3 480" + 4" = 122 284"
3) Utilizando la forma decimal expresa :
a) En grados : 55º 42' 30'' b) En grados : 120º 15' 40''
c) En minutos : 90º 37' 6'' d) En minutos : 35º 55' 17''
a)
55º 42' 30'' → 55º + 42 : 60 + 30 : 3 600 = 55 + 0,7 + 0,0083 = 55,7083º
b)
120º 15' 40'' → 120 + 15 : 60 + 40 : 3600 = 120 + 0,25 + 0,0111 = 120,2611º
c)
90º 37' 6'' → 90 · 60 + 37 + 6 : 60 = 5400 + 37 + 0,1 = 5437,1'
d)
35º 55' 17'' → 35 · 60 + 55 + 17 : 60 = 2100 + 55 + 0,2833 = 2155,2833'
5) Efectúa las siguientes operaciones con ángulos :
a) 24º 35' 19" + 16º 13' 31" b) 14º 28' 45" + 30º 34' 26"
c) 27º 36' 12" + 41º 39' 55" d) 47º 39' 52" - 17º 26' 20"
e) 38º 6' 18" - 11º 32' 51" f) 90º - 19º 52' 23"
g) 180º - 147º 31' 9" h) 270º - 100º 16' 38"
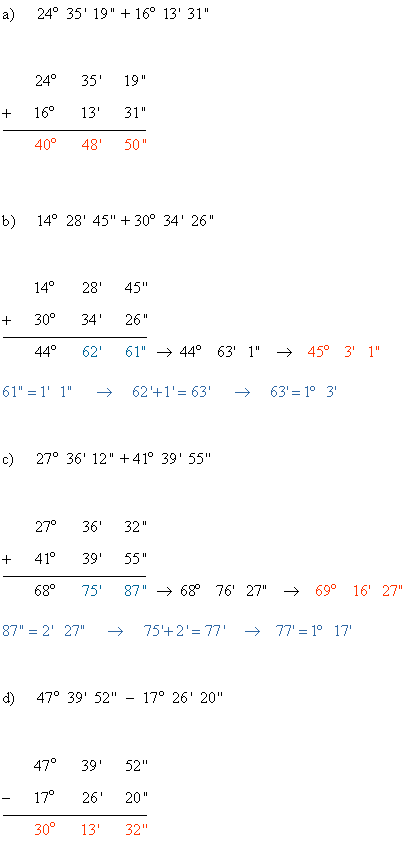
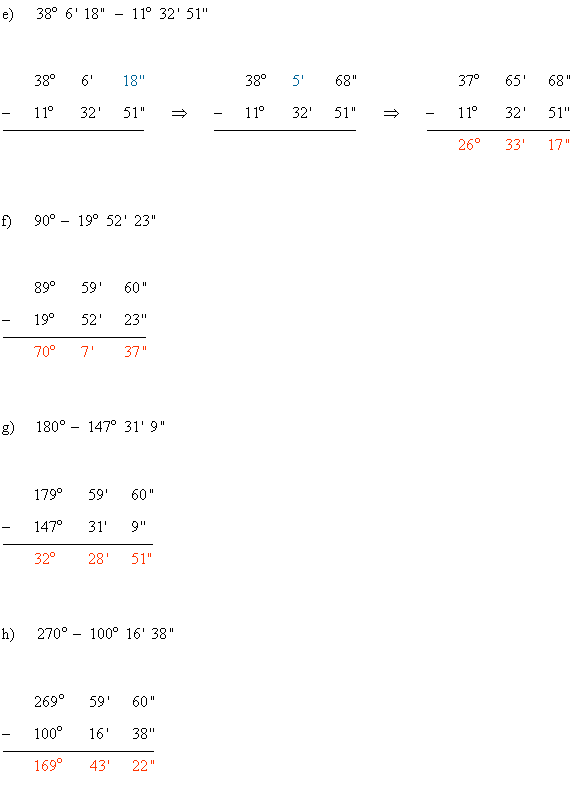
6) Efectúa las siguientes operaciones con ángulos :
a) ( 14º 8' 11" ) · 3 b) ( 21º 28' 17" ) · 5
c) ( 32º 30' 15") · 4 d) ( 145º 35' 52" ) : 5
e) ( 36º 47' 25" ) : 5 f) ( 145º 35' 48" ) : 12


7) Halla el doble, el triple y el cuadruple del ángulo 43º 17' 55"
Doble :
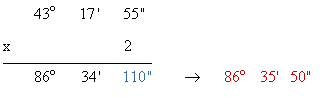
110" = 1' 50" → 34' + 1' = 35'
Triple :
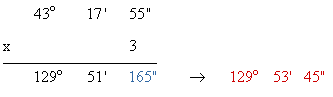
165" = 2' 45" → 51' + 2' = 53'
Cuadruple :
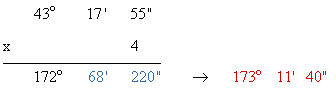
220" = 3' 40" → 68' + 3' = 71' → 71' = 1º + 11' → 172º + 1º = 173º
8) En el ángulo
= 75º 41' 30" trazamos su bisectriz. ¿Cuánto mide cada ángulo restante?
Como trazamos su bisectriz, tenemos que dividir el ángulo entre dos.
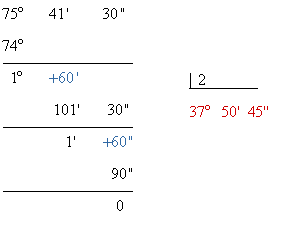
→
Cada uno de los ángulos mide 37º 50' 45"
9) Obtén en ángulo complementario y suplementario de los siguientes ángulos :
a) 35º b) 20º c) 59º 23' d) 87º 39' 45"
a)
Complementario : 90º - 35º = 55º Suplementario : 180º - 35º = 145º
b)
Complementario : 90º - 20º = 70º Suplementario : 180º - 20º = 160º
c)
Complementario : 90º - 59º 23' → 89º 60' - 59º 23' = 30º 37'
Suplementario : 180º - 59º 23' → 179º 60' - 59º 23' = 120º 37"
d)
Complementario : 90º - 87º 39' 45" → 89º 59' 60" - 87º 39' 45" = 2º 20' 15"
Suplementario : 180º - 87º 39' 45" → 179º 59' 60" - 87º 39' 45" = 92º 20' 15"
10) Dados los ángulos
= 48º 31' 27" y
= 25º 11' 15" determina el valor de de las amplitudes de estos ángulos :
a)+
b)
-
c) 2 ·
d) El complementario de+
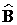
e) El suplementario de-
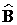
f) El suplementario de 2 ·
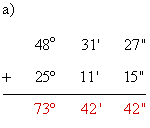
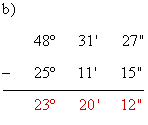
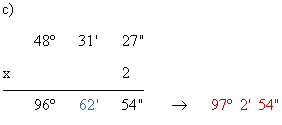
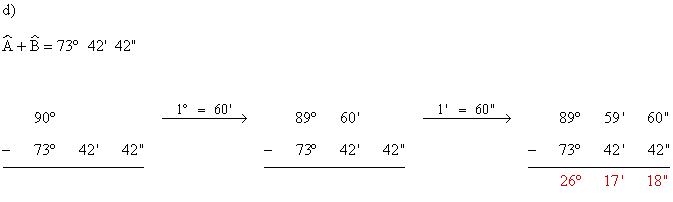
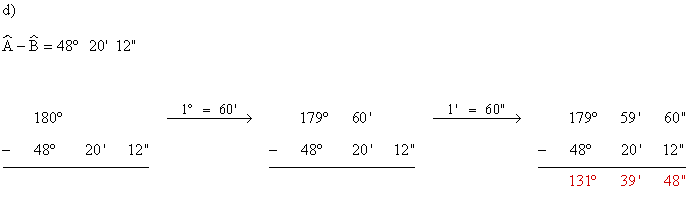
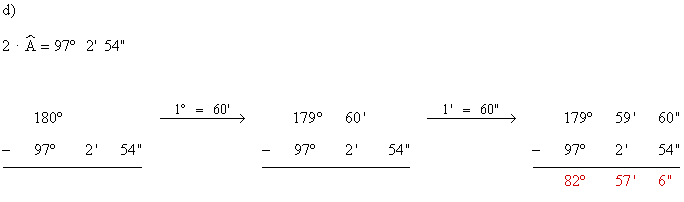
11) Dos ángulos son suplementarios y uno vale el doble que el otro. Halla el valor de dichos ángulos.
Un ángulo es x y el otro por ser el doble es 2 · x. Como son suplementarios tenemos que :
x + 2 · x = 180 → 3 · x = 180 → x = ![]() = 60
= 60
Un ángulo mide 60º y el otro mide 120º .
12) Dos ángulos son complementario y uno vale el cuádruple del otro. Halla el valor de dichos ángulos.
Llamamos x a uno de los ángulos y el otro, como es el cuádruple de este, es 4 · x. Como son complementarios tenemos que :
x + 4 · x = 90 → 5 · x = 90 → x = ![]() = 18
= 18
Un ángulo mide 18º y el otro mide 72º .
13) Determina la medida de estos dos ángulos, y resuelve las operaciones que se indican :

a)b)
c)
d)
a) b) c) d)
90º + 270º = 360º 270º - 90º = 180º 3 · 270º = 810º 4 · 90º = 360º
14) Calcula la amplitud del ángulo X en cada figura :

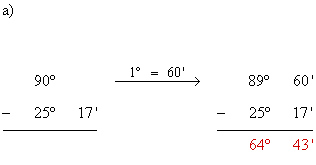
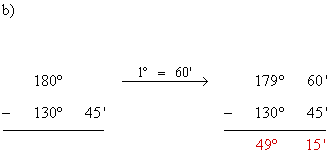
15) Calcula el valor exacto de los ángulos que forman la aguja horaria y el minutero de un reloj a las horas siguientes :
a) A las 4 de la mañana.
b) A las 4 y cuarto.
c) A las 4 y media.
d) A las 2 y 20 minutos.
Minutero :
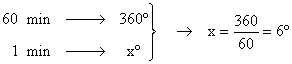 La aguja del minutero recorre 6º en cada minuto.
La aguja del minutero recorre 6º en cada minuto.
Horaria :
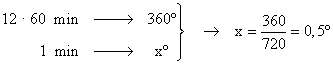 La aguja horaria recorre 0,5º cada minuto.
La aguja horaria recorre 0,5º cada minuto.
a)
Minutero → 0º
Horaria → 4 · 60 · 0,5 = 120º
El ángulo que forman es 120º
b)
Minutero → 15 · 6 = 90º
Horaria → ( 4 · 60 + 15 ) · 0,5 = 255 · 0,5 = 127,5
El ángulo que forman es : 127,5º - 90º = 37,5º
c)
Minutero → 30 · 6 = 180º
Horaria → ( 4 · 60 + 30 ) · 0,5 = 270 · 0,5 = 135º
El ángulo que forman es : 180º - 135º = 45º
d)
Minutero → 20 · 6 = 120º
Horaria → ( 2 · 60 + 20 ) · 0,5 = 140 · 0,5 = 70º
El ángulo que forman es : 120º - 70º = 50º


 INICIO
INICIO