Ejercicios resueltos de ángulos en polígonos.
1) Calcula la medida del ángulo B de los siguientes polígonos.
a)b)
2) Calcula la medida del ángulo B de los siguientes polígonos :
a)b)
3) Calcula la medida del ángulo B en los siguientes polígonos :
a)b)
4) Calcula las medidas de los ángulo A, B y C de los siguientes polígonos :
a)b)
5) Calcula las medidas de los ángulo A, B y C de los siguientes polígonos.
a)b)
6) Calcula la medida de los ángulos desconocidos de los siguientes polígonos.
a)b)

c)d)
7) Calcula los ángulos del siguiente polígono irregular.
8) Averigua cuánto miden los ángulos señalados en el siguiente pentágono :
9) Calla los ángulos inscritos de los siguientes polígonos :
a)b)
10) Construye un triángulo como este con las siguientes medidas : a = 5 cm ; A = 40º ; B = 100º
Halla los ángulos D y E. ¿Cómo son los ángulos B y E ? ¿ Y D y C ?
11) Calcula el valor del ángulo B del siguiente cuadrilátero :
12)
1) Calcula la medida del ángulo B de las siguientes figuras.
a)b)
a)
El ángulo adyacente al de 70º es suplementario luego su valor es de 180º - 70º = 110º.
Como los ángulos de un triángulo suman 180º, entonces el valor de B es B = 180º - 110º - 35º = 35º
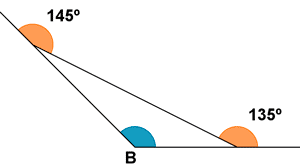
b)
Los ángulos adyacentes, y por tanto suplementarios, de los ángulos 145º y 135º son, respectivamente 35º y 45º.
Como los ángulos de un triángulo tienen que sumar 180º tenemos que : B = 180º - 35º - 45º = 100º
2) Calcula la medida del ángulo B de las siguientes figuras :
a)b)

a)
Los ángulos adyacentes ( suplementarios ) de los ángulos 155º y 145º son, respectivamente, 25º y 35º.
Los ángulos de un triángulo suman 180º por lo que el valor de B es : B = 180º - 35º - 25º = 120º
b)
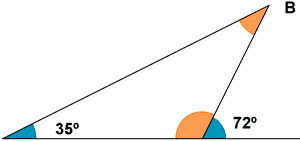
El ángulo adyacente a 72º es 108º.
La suma de los ángulos del triángulo ha de ser 180º. El valor de B es : B = 180º - 35º - 108º = 37º
3) Calcula la medida del ángulo B en las siguientes figuras :
a)b)

a)
El valor del ángulo adyacente o suplementario de 128º es 52º.
El ángulo opuesto a 47º, por ser agudo y paralelo a él vale 47º.
Por último, la suma de los ángulos del triángulo que forma la mitad del cuadrilátero ha de sumar 180º por lo que el valor de B es : B = 180º - 47º - 52º = 81º
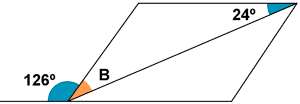
b)
El ángulo opuesto a 126º también vale 126º, ya que ambos son obstusos y con lados paralelos.
La suma de los ángulos del triángulo formado por el semicuadrilatero tiene que ser 180º, de modo que B vale : B = 180º - 126º - 24º = 30º
4) Calcula las medidas de los ángulo A, B y C de las siguientes figuras :
a)b)
a)
El ángulo B se corresponde con el ángulo central del triángulo. Su valor es : ![]()
El ángulo A se corresponde con el ángulo interior del triángulo : A = 180º - B → A = 180º - 120º = 60º
El ángulo C se corresponde con el ángulo exterior del triángulo : C = 360º - A → C = 360º - 60º = 300º
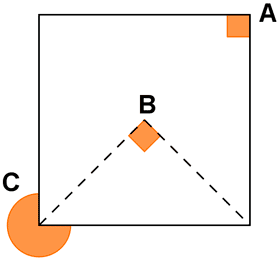
b)
El ángulo B se corresponde con el ángulo central del cuadrado. Su valor es : ![]()
El ángulo A se corresponde con el ángulo interior del cuadrado : A = 180º - B → A = 180º - 90º = 90º
El ángulo C se corresponde con el ángulo exterior del cuadrado : C = 360º - A → C = 360º - 90º = 270º
5) Calcula las medidas de los ángulo A, B y C de las siguientes figuras.
a)b)

a)
El ángulo A es el ángulo central del hexágono, su valor es : ![]()
Cada ángulo interno de un polígono regular de n lados mide ![]() por lo que en el caso del hexágono cada uno de ellos mide :
por lo que en el caso del hexágono cada uno de ellos mide : ![]()
Luego B = 120º
El ángulo C se corresponde con el ángulo exterior del hexágono : C = 360º - B → C = 360º - 120º = 240º
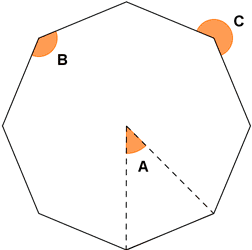
b)
El ángulo A es el ángulo central del octógono, su valor es : ![]()
El ángulo B es el ángulo interior del octógono, su valor es : ![]()
El ángulo C se corresponde con el ángulo exterior del octógono : C = 360º - B → C = 360º - 135º = 225º
6) Calcula la medida de los ángulos desconocidos de las siguientes figuras.
a)b)

c)d)

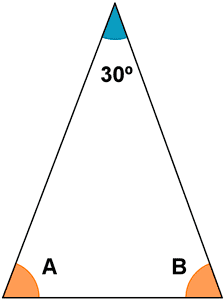
a)
C = 28º
A = B = 180º - 28º = 152º
b)
![]()
c)
A = 180º - 45º = 135º
d)
![]()
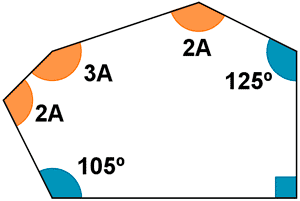
7) Calcula los ángulos del siguiente polígono irregular.

La suma de los ángulos internos de un polígono es : 180º · ( n - 2 ). Luego tenemos que :
2A + 2A + 3A + 105º + 125º + 90º = 180º · ( 6 - 2 ) →
7A + 320º = 720º → 7A = 400º → A = 57,14º
Los ángulos pedidos son 114,28º ; 114,28º
; 171,42º
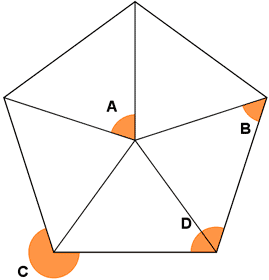
8) Averigua cuánto miden los ángulos señalados en el siguiente pentágono :
El ángulo A es el ángulo central del pentágono, su valor es : ![]()
El ángulo D es el ángulo interior del pentágono, su valor es : ![]()
El ángulo B es la mitad del ángulo interior del pentágono, es decir, el ángulo D. Su valor es : ![]()
EL ángulo C se corresponde con el ángulo exterior del pentágono : C = 360º - D → C = 360º - 108º = 252º
9) Calla los ángulos inscritos de los siguientes polígonos :
a)b)
a)
La circunferencia en la que está inscrito el hexágono ha quedado dividida en seis arcos, cada uno de 60º. Los ángulos son inscritos, por lo que miden la mitad del arco que abarcan.
El ángulo A abarca cuatro arcos por lo que su medida es : ![]()
El ángulo B abarca un arco, por lo que su medida es : ![]()
El ángulo C abarca tres arcos. Su medida es : ![]()
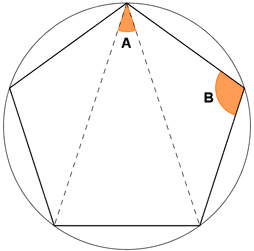
b)
En este caso, la circunferencia en la que está inscrita el pentágono, queda dividida en cinco arcos, cada uno de ellos con una amplitud de 72º. Los ángulos son inscritos, por lo que su medida es la mitad de los arcos que abarcan.
El ángulo A abarca un arco por lo que su medida es : ![]()
El ángulo B abarca tres arcos. Su medida es : ![]()
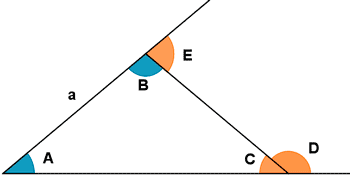
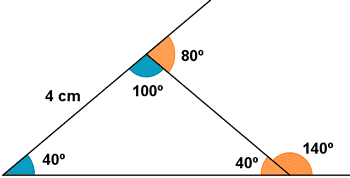
10) Construye un triángulo como este con las siguientes medidas : a = 5 cm ; A = 40º ; B = 100º
Halla los ángulos D y E. ¿Cómo son los ángulos B y E ? ¿ Y D y C ?
Los ángulos A, B y C forman un triángulo por lo que su suma tiene que ser 180º : A + B + C = 180º → 40º + 100º + C = 180º → C = 40º
B y E son adyacentes y por lo tanto suplementarios, han de sumar entre ambos 180º : B + E = 180º → 100º + E = 180º → E = 80º
Con los ángulos C y D ocurre lo mismo, son adyacentes y suplementarios : C + D = 180º → 40º + D = 180º → D = 140º
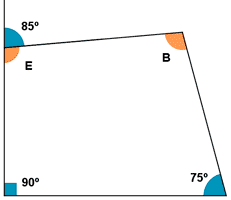
11) Calcula el valor del ángulo B del siguiente cuadrilátero :

El ángulo E es el ángulo adyacente o complementario de 85º, por lo que juntos tienen que sumar 180º. Su valor es : E = 180º - 85º = 95º
Como los ángulos de un cuadrilátero suman 360º, entonces B vale : B = 360º - 90º - 75º - 95º = 360º - 260º = 100º


 INICIO
INICIO