Ejercicios y problemas resueltos de traslaciones y giros.
1)
Realiza una traslación del punto A ( -1, 4) según el vector 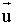 = ( 5, -2 ) .
= ( 5, -2 ) .
2) Calcula los componentes del vector de traslación que transforma el punto A ( 6, 3 ) en A' ( 4, - 1 ).
3)
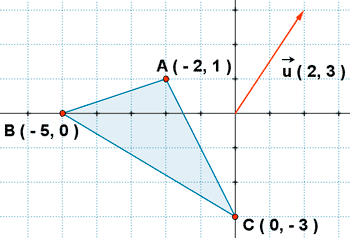
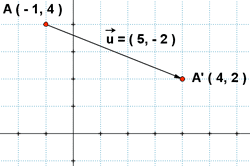
Observa el triángulo y el vector de la figura. Indica las coordenadas de los puntos A', B' y C' producto de trasladar el triángulo según el vector 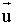 .
.
4)
Representa en unos ejes de coordenadas el vector 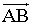 , siendo A ( 2, 1 ) y B ( 6, 3 ). Aplica a dicho vector una traslación según el vector
, siendo A ( 2, 1 ) y B ( 6, 3 ). Aplica a dicho vector una traslación según el vector 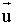 = ( 2, - 3 ).
= ( 2, - 3 ).
5)
Las coordenadas de los vértices de un triángulo ABC son A ( 1, 6 ), B ( 1, 2 ) y C ( 3, 4 ). Hallar los vértices del triángulo obtenido aplicando sucesivamente las traslaciones de vectores guía 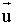 = ( 4, 2 ) y
= ( 4, 2 ) y 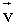 = ( 3, - 3 ).
= ( 3, - 3 ).
6)
Representa el cuadrilátero de vértices A ( - 5, 2 ), B ( - 3, - 1 ), C ( 2, 1 ) y D ( 0, 4 ). Traslada dicho cuadrilátero según el vector 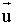 ( 9, 3 ).
( 9, 3 ).
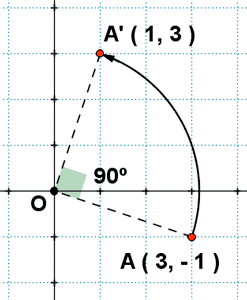
7) Calcula las coordenadas del punto A' resultante de aplicar al punto A ( 3, - 1 ) un giro de 90º con centro en el origen de coordenadas.
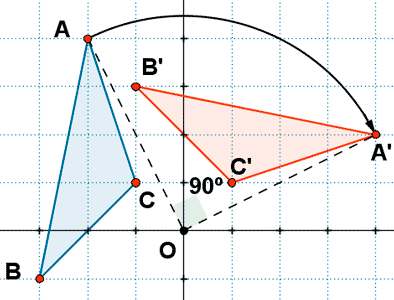
8) Dado el triángulo ABC cuyas coordenadas son A ( - 2, 4 ), B ( - 3, - 1 ) y C ( - 1, 2 ) representa su triángulo homólogo al aplicarle un giro de - 90º cuyo centro es el origen de coordenadas.
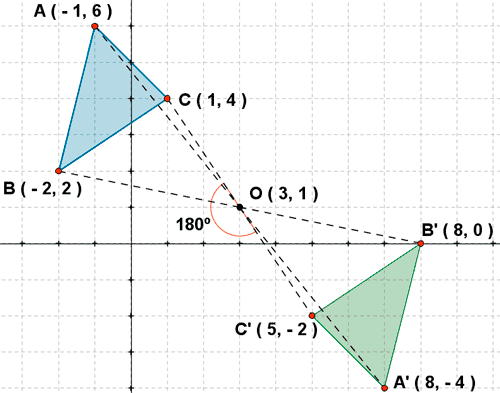
9) Un triángulo tiene por vértices los puntos A ( -1, 6 ) , B ( - 2, 2 ) y C ( 1, - 4 ). Halla su triángulo transformado por un grio de centro ( 3, 1 ) y ángulo 180º.
1)
Realiza una traslación del punto A ( -1, 4) según el vector 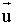 = ( 5, -2 ) .
= ( 5, -2 ) .
A' = ( x + u 1 , y + u 2 ) = ( - 1 + 5 , 4 - 2 ) = ( 4 , 2 )
2) Calcula los componentes del vector de traslación que transforma el punto A ( 6, 3 ) en A' ( 4, - 1 ).
Las coordenadas de la traslación del punto A ( x, y ) mediante el vector ![]() = ( u 1 , u 2 ) son A' ( x + u 1 , y + u 2 ).
= ( u 1 , u 2 ) son A' ( x + u 1 , y + u 2 ).
Se tiene que cumplir por tanto :
6 + u 1 = 4 y 3 + u 2 = -1 → u 1 = -2 y u 2 = - 4.
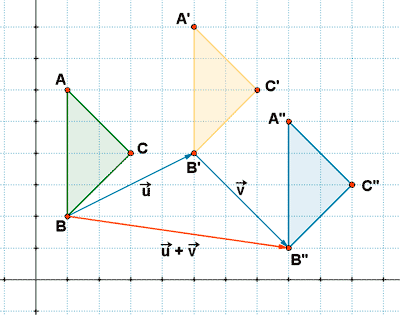
3)
Observa el triángulo y el vector de la figura. Indica las coordenadas de los puntos A', B' y C' producto de trasladar el triángulo según el vector  .
.

A' = ( - 2 + 2, 1 + 3 ) = ( 0, 4 )
B' = ( - 5 + 2, 0 + 3 ) = ( - 3, 3 )
C' = ( 0 + 2, - 3 + 3 ) = ( 2, 0 )
4)
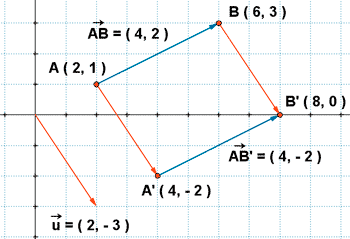
Representa en unos ejes de coordenadas el vector 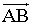 , siendo A ( 2, 1 ) y B ( 6, 3 ). Aplica a dicho vector una traslación según el vector
, siendo A ( 2, 1 ) y B ( 6, 3 ). Aplica a dicho vector una traslación según el vector 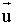 = ( 2, - 3 ).
= ( 2, - 3 ).
5)
Las coordenadas de los vértices de un triángulo ABC son A ( 1, 6 ), B ( 1, 2 ) y C ( 3, 4 ). Hallar los vértices del triángulo obtenido aplicando sucesivamente las traslaciones de vectores guía  = ( 4, 2 ) y
= ( 4, 2 ) y 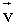 = ( 3, - 3 ).
= ( 3, - 3 ).
El vector de traslación es :
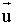 +
+ 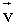 = ( 4 + 3, 2 - 3 ) = ( 7, - 1 )
= ( 4 + 3, 2 - 3 ) = ( 7, - 1 )
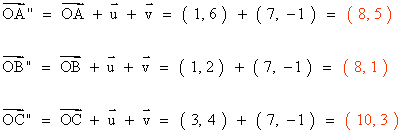
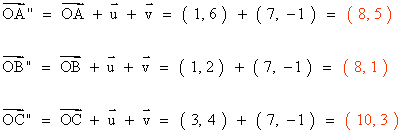
6)
Representa el cuadrilátero de vértices A ( - 5, 2 ), B ( - 3, - 1 ), C ( 2, 1 ) y D ( 0, 4 ). Traslada dicho cuadrilátero según el vector 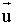 ( 9, 3 ).
( 9, 3 ).
7) Calcula las coordenadas del punto A' resultante de aplicar al punto A ( 3, - 1 ) un giro de 90º con centro en el origen de coordenadas.
8) Dado el triángulo ABC cuyas coordenadas son A ( - 2, 4 ), B ( - 3, - 1 ) y C ( - 1, 2 ) representa su triángulo homólogo al aplicarle un giro de - 90º cuyo centro es el origen de coordenadas.
9) Un triángulo tiene por vértices los puntos A ( -1, 6 ) , B ( - 2, 2 ) y C ( 1, - 4 ). Halla su triángulo transformado por un grio de centro ( 3, 1 ) y ángulo 180º.


 INICIO
INICIO