Giros.
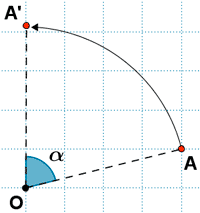
Un giro de centro O y ángulo α es un movimiento que convierte un punto A en otro A' de modo que OA = OA' y el ángulo formado por AOA' es igual a α.
Se representa por G ( O, α )
Ángulos de giro positivos o negativos.
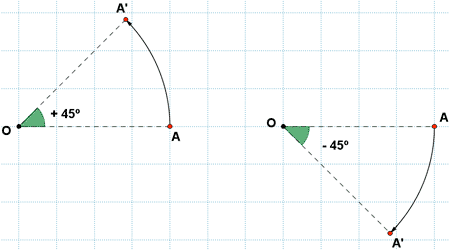
G ( O, +45º)
G' ( O, - 45º)
Los ángulos de giro pueden ser positivos, cuando giramos en sentido contrario a las agujas del reloj, o negativos, cuando giramos en el sentido de las agujas del reloj.
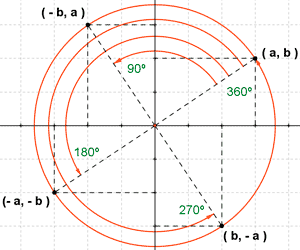
Un punto ( a, b ) situado en unos ejes de coordenadas se transforma en ( -b, a) por un giro G ( O ( 0, 0 ) ; 90º ).
Si el giro es G ( O ( 0, 0 ) ; 180º ) el punto ( a, b ) se transforma en ( - a, - b ).
Si el giro es G ( O ( 0, 0 ) ; 270º ) el punto ( a, b ) se transforma en ( b, - a ).
Si el giro es G ( O ( 0, 0) ; 360º ) el punto ( a, b ) se transforma en ( a, b ).
Giro de una figura.
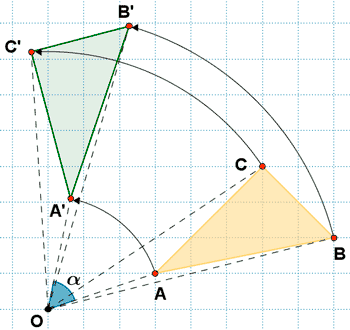
Ejemplo de giro de un triángulo con coordenadas geométricas.
Un triángulo tiene por vértices los puntos A ( -1, 6 ) , B ( - 2, 2 ) y C ( 1, - 4 ). Halla su triángulo transformado por un grio de centro ( 3, 1 ) y ángulo 180º.
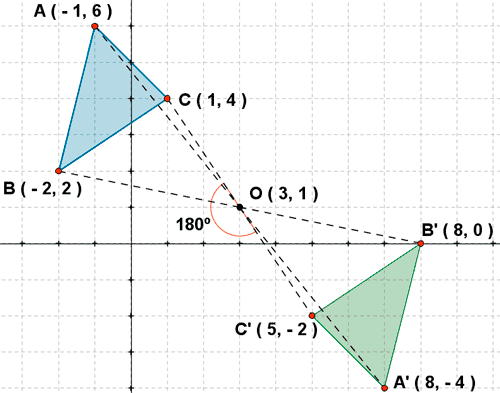
Propiedades del giro.
- EL giro es una transformación isométrica, por tanto, se conserva las propiedades métricas, es decir, la forma y el tamaño.
- El giro conserva la distancia.
- Conserva los ángulos.
- El sentido de la figura se conserva, luego decimos que es un movimiento directo de plano.
Determinación del centro y ángulo de un giro.
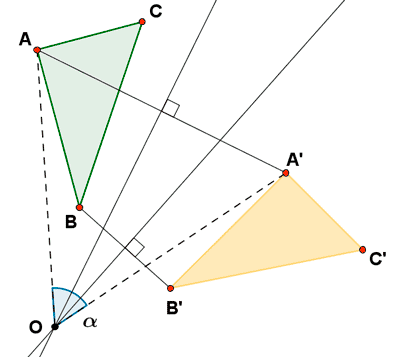
1.- Trazamos los dos segmentos que unen dos puntos homólogos, por ejemplo, AA' y BB'.
2.- Trazamos la mediatriz del segmento AA' y del segmento BB'.
El punto de intersección de las dos mediatrices es el centro de giro O.
3.- Una vez determinado el centro de giro, para obtener el ángulo de giro basta con medir el ángulo AOA'.


 INICIO
INICIO

