Traslaciones en el plano.
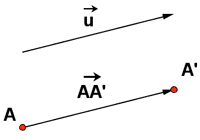
Una traslación de vector ![]() es un movimiento en el plano que transforma un punto A en otro A'.
es un movimiento en el plano que transforma un punto A en otro A'.
El vector ![]() tienen la misma longitud, dirección y sentido que el vector
tienen la misma longitud, dirección y sentido que el vector ![]() .
.
Las coordenadas de la traslación del punto A ( x, y ) mediante el vector ![]() = ( u 1 , u 2 ) son A' ( x + u 1 , y + u 2 ).
= ( u 1 , u 2 ) son A' ( x + u 1 , y + u 2 ).
( x', y' ) = ( x, y ) + ( u 1 , u 2 ) → 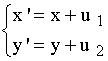
Ejemplo 1 :
Traslada los puntos A ( -1 , 3 ) ; B ( 3, 3 ) y C ( 2 , - 4 ) según el vector ![]() = ( 5 , - 1 ) .
= ( 5 , - 1 ) .
A' = ( x + u 1 , y + u 2 ) = ( -1 + 5 , 3 - 1 ) = ( 4 , 2 ).
B' = ( x + u 1 , y + u 2 ) = ( 3 + 5 , 3 - 1 ) = ( 8 , 2 )
C' = ( x + u 1 , y + u 2 ) = ( 2 + 5 , - 4 - 1 ) = ( 7 , - 5 )
Si aplicamos el proceso de traslación a un conjunto de puntos, podemos trasladar cualquier figura que deseemos.
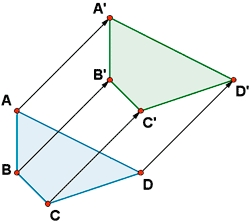
Ejemplo 2 :
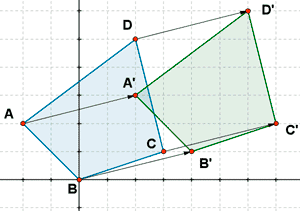
Traslada la figura de coordenadas A ( - 2 , 2 ) ; B ( 0 , 0 ) ; C ( 3 , 1 ) y D ( 2 , 5 ) según el vector ![]() = ( 4 , 1 ) .
= ( 4 , 1 ) .
A' = ( - 2 + 4 , 2 + 1 = ( 2 , 3 )
B' = ( 0 + 4 , 0 + 1 ) = ( 4 , 1 )
C' = ( 3 + 4 , 1 + 1 ) = ( 7 , 2 )
D' = ( 2 + 4 , 5 + 1 ) = ( 6 , 6 )
Propiedades de las traslaciones.
- La traslación es una transformación isométrica, por tanto, se conserva las propiedades métricas, es decir, la forma y el tamaño.
- Una recta se transforma en otra recta paralela.
- El sentido de la traslación se conserva luego decimos que la traslación es un movimiento directo del plano. El sentido de la figura se conserva.


 INICIO
INICIO

