Ángulos en los polígonos.
Número de diagonales.
El número de diagonales de un polígono de n vértices es:
![]()
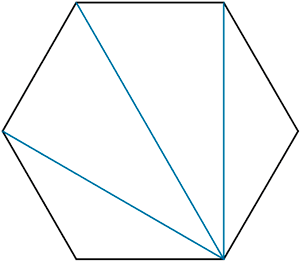
Suma de los ángulos de un hexágono.
Mediante diagonales descomponemos un hexágono en cuatro triángulos. Como los ángulos de un triángulo suman 180º, al tener cuatro triángulos tendremos 180º · 4 por tanto los ángulos de todos los hexágonos suman 720º.
Cada ángulo de un hexágono regular (todos sus ángulos son iguales) mide 720º / 6 = 120º
Suma de los ángulos interiores de polígono cualquiera.
Un polígono de n lados se puede descomponer en (n-2) triángulos. La suma de todos sus ángulos es (n - 2) · 180º
Cada ángulo de un polígono regular de n lados mide :
![]()
Ejemplo 1:
Calcular el número de diagonales y el valor de los ángulos de un heptágono regular.
Un heptágono es un polígono de 7 vértices, por tanto n = 7
Aplicamos la fórmula para obtener el número de diagonales:
![]()
Por ser regular, todos los ángulos miden lo mismo, por tanto la fórmula para obtener el ángulo será:
![]()
Ejemplo 2:
Calcular el número de diagonales , la suma de los ángulos y el valor de los ángulos de un octógono regular.
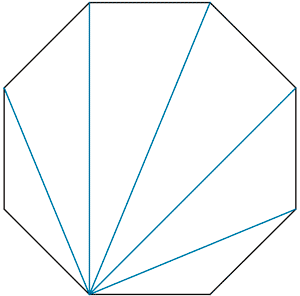
Un octógono es un polígono de 8 vértices, por tanto n = 8
![]()
El octógono se puede descomponer mediante diagonales en seis triángulos, sus ángulos sumarán por tanto (n - 2) · 180º = 6 · 180º = 1080º
Luego en un octógono regular cada ángulo medirá
![]()
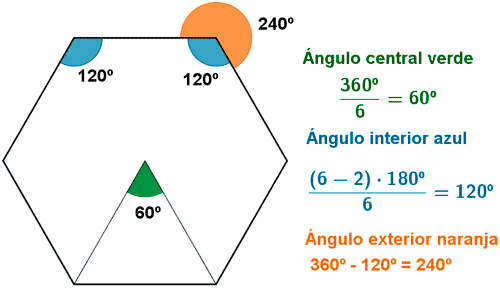
El ángulo central de un polígono regular.
El valor de un ángulo central de un polígono regular de n lados es igual a
![]()
El ángulo exterior de un polígono regular.
Es igual a 360º menos su ángulo interior:
![]()
Ejemplo 3:
Halla el ángulo central, el ángulo interior y el ángulo exterior de un hexágono regular.
Ángulo y diagonales de los polígonos regulares.
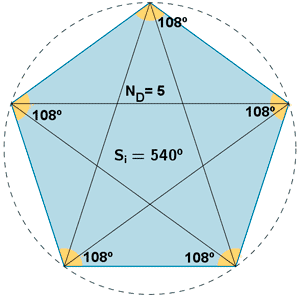
| Polígono | Lados | Ángulo central | Ángulo interior | Suma de ángulos interiores (Si ) | Número de diagonales (ND ) |
|---|---|---|---|---|---|
| Pentágono | 5 | ||||
| Hexágono | 6 | ||||
| Octógono | 8 | ||||
| Dodecágono | 12 | ||||
| n lados | n |


 INICIO
INICIO

