Ángulos
Ángulo en el plano
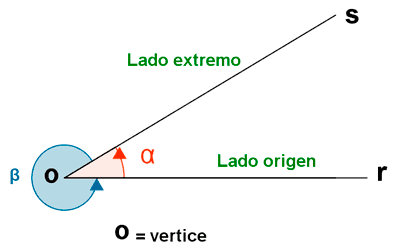
Dos semirrectas, r y s , con un origen común O divide el plano en dos regiones, cada una de las cuales determina un ángulo. De esta forma, O es el vértice de los ángulos α y β
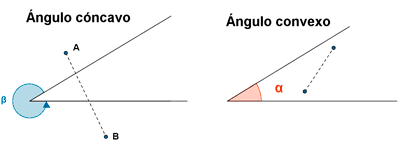
Clasificación de ángulos
| Terminología | Definición | Ejemplos |
|---|---|---|
| Ángulo completo α | α = 360o | 360o |
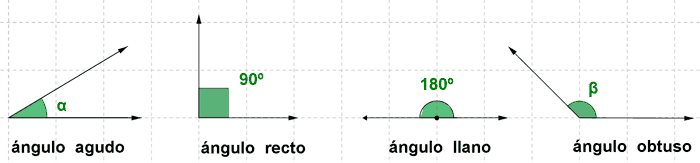
| Ángulo llano α | α = 180o | 180o |
| Ángulo recto α | α = 90o | 90o |
| Ángulo agudo α | 0o < α < 90o | 15o , 37o , 85o |
| Ángulo obtuso α | 90o < α < 180o | 105o , 99o , 145o |
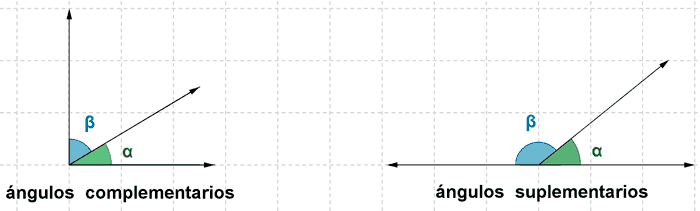
| Ángulos complementarios α , β | α + β = 90o | 30o y 60o , 15o y 75o |
| Ángulo suplementarios α , β | α + β = 180o | 110o y 70o , 15o y 165o |
Ampliación del concepto de ángulo
Criterio de orientación de ángulos:
ángulos positivos y ángulos negativos
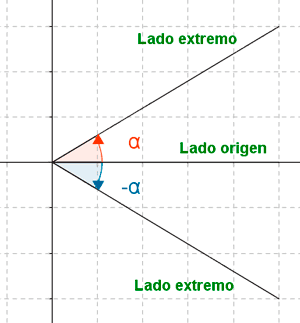
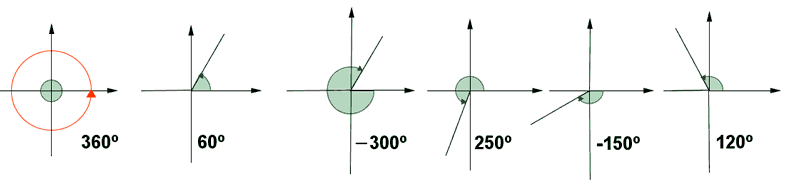
Un ángulo α está orientado en sentido positivo cuando el giro desde la semirrecta origen a la semirrecta extremo se realiza en el sentido opuesto al de las agujas del reloj.
Si el giro se realiza a favor de las agujas del reloj se dice que el ángulo está orientado en sentido negativo.
Reducción de ángulos al primer giro:
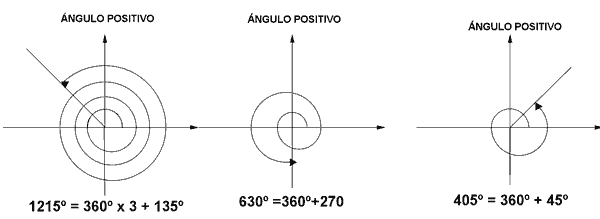
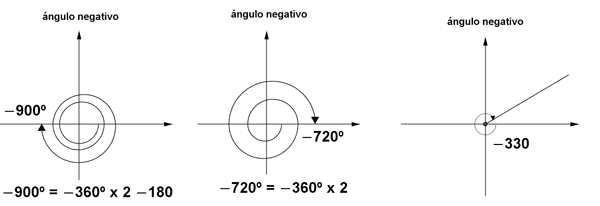
ángulos mayores de 360o
Para representar geométricamente un ángulo mayor de 360o, se le restan tantas vueltas como sea posible, resultando por tanto un ángulo comprendido entre 0o y 360o.
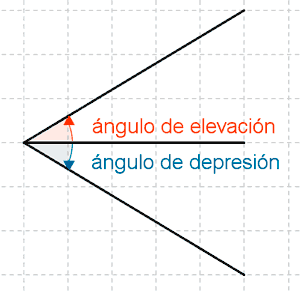
Ángulo de elevación y ángulo de depresión


 INICIO
INICIO
