Ejercicios resueltos de ángulos en la circunferencia.
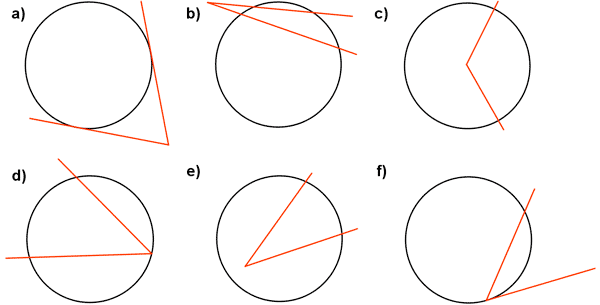
1) Di qué tipo de ángulos son los siguientes respecto de las circunferencias en las que se encuentran.
2) Calcula la medida del ángulo central cuando el ángulo inscrito en una circunferencia mide :
a) 25º b) 40º c) 60º d) 75º
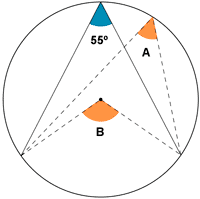
3) Calcular los ángulos naranjas de los siguientes círculos :
a)b)
4) Calcular los ángulos naranjas señalados en el siguiente círculo.
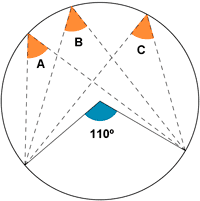
5) Calcular los ángulos de la siguientes figuras:.
a) A, B y C:b) A, B, C, D, E y F:
6) Halla el valor de los siguientes ángulos indicados en naranja:
a)b)
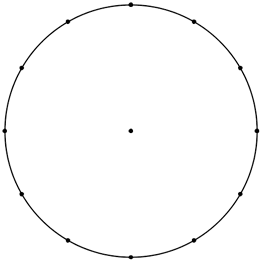
7) Copia la figura y construye a partir de ella los ángulos inscritos cuyas medidas son las siguientes :
a) 15º b) 30º c) 45º d) 60º
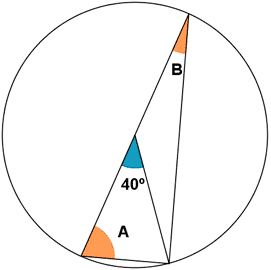
8) Calcula los ángulos A y B indicados en la siguiente figura :
9) Obtén la medida del ángulo representado en la siguiente circunferencia :
10) Calcula en cada caso la medida del ángulo B :
a)b)
c)
11)
12)
1) Di qué tipo de ángulos son los siguientes respecto de las circunferencias en las que se encuentran.

a) Ángulo circunscrito.
b) Ángulo exterior.
c) Ángulo central.
d) Ángulo inscrito.
e) Ángulo interior.
f) Ángulo semiinscrito.
2) Calcula la medida del ángulo central cuando el ángulo inscrito en una circunferencia mide :
a) 25º b) 40º c) 60º d) 75º
El valor del ángulo central de una circunferencia es el doble de un ángulo inscrito en ella. Por lo tanto, los ángulos pedidos son :
a) 2 · 25º = 50º
b) 2 · 40º = 80º
c) 2 · 60º = 120º
d) 2 · 75º = 150º
3) Calcular los ángulos indicados de los siguientes círculos :
a)b)
a) b)

4) Calcular los ángulos incógnitas señalados en el siguiente círculo.

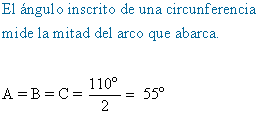
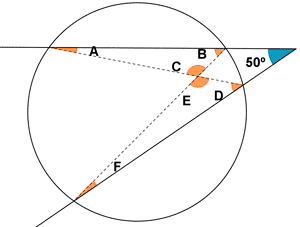
5) Calcular los ángulos A, B y C de la siguiente figura.
a)b)
a) 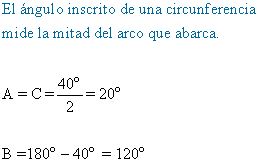 b)
b) 
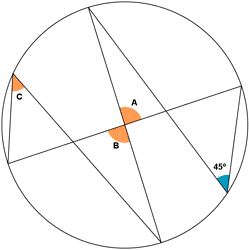
6) Halla el valor de los siguientes ángulos indicados :
a)b)
a)
![]()
b)
A = B = 45º · 2 = 90º
C = 45º
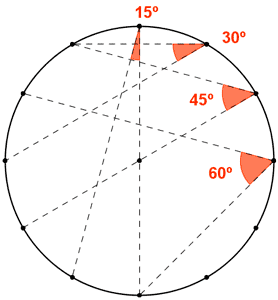
7) Copia la figura y construye a partir de ella los ángulos inscritos cuyas medidas son las siguientes :
a) 15º b) 30º c) 45º d) 60º

La circunferencia está dividida en 12 partes, cada una de ellas con una amplitud de 30º. Como queremos construir ángulos inscritos, su medida es la mitad de partes que abarquen. Es decir, si queremos dibujar un ángulo inscrito de 15º, este deberá abarcar 15 · 2 = 30º que en este caso es una parte de las 12 en las que está dividida la circunferencia.
8) Calcula los ángulos A y B indicados en la siguiente figura :

El ángulo B es un ángulo inscrito en la circunferencia, por lo que su medida es la mitad del ángulo central : ![]()
El arco correspondiente al ángulo A es igual al ángulo suplementario de 40º, es decir : 180º - 40º = 140º.
La amplitud de A, al ser inscrito, es la mitad de este : ![]()
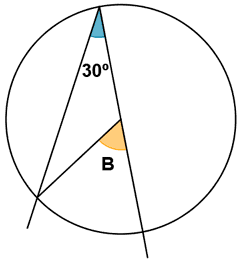
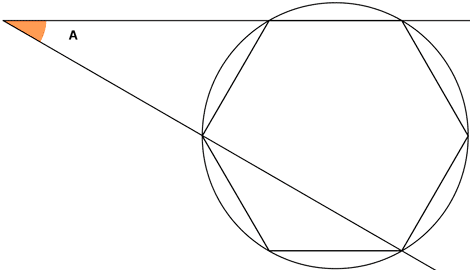
9) Obtén la medida del ángulo representado en la siguiente circunferencia :

El valor de un ángulo exterior viene determinado por la mitad del ángulo central que forma menos la mitad del ángulo inscrito que forma, es decir, la mitad del ángulo C menos la mitad del ángulo B :
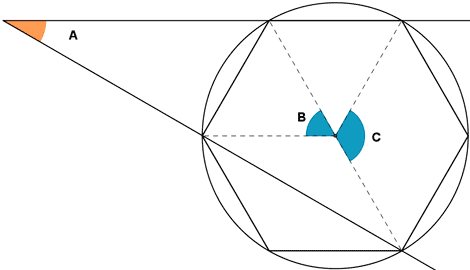
La circunferencia queda dividida en seisarcos, cada uno de ellos de 60º. Como B abarca un arco su medida es 60º mientras que C abarca dos y su medida es 120º. Por tanto, el valor del ángulo A es : ![]()
10) Calcula en cada caso la medida del ángulo B :
a)b)
c)
a)
El ángulo es un ángulo inscrito que abarca un arco de 180º. Su medida es B = 180 : 2 = 90º
b)
Por ser un ángulo inscrito, su medida es la mitad del ángulo que abarca, luego B = 80 : 2 = 40º
c)
En este caso, el ángulo de 30º está inscrito en la circunferencia. La medida de B será el doble de este, luego B = 30 · 2 = 60º


 INICIO
INICIO