Problemas resueltos de distribuciones de la proporción y distribuciones en la diferencia de las medias.
1) Se sabe que el 10 % de los habitantes de una determinada ciudad va regularmente al teatro. Se toma una muestra al azar de 100 habitantes de esta ciudad, ¿cuál es la probabilidad aproximada de que al menos el 13 % de ellos vaya regularmente al teatro?
2) Un estudio realizado por una compañia de seguros de automóviles establece que una de cada cinco personas accidentadas es mujer. Si se contabilizan, por término medio, 169 accidentes cada fin de semana :
a) ¿Cuál es la probabilidad de que, en un fin de semana, la proporción de mujeres accidentadas supere el 24 % ?
b) ¿Cuál es la probabilidad de que, en un fin de semana, la proporción de hombres accidentados supere el 85 % ?
c) ¿Cuál es, por término medio, el número esperado de hombres accidentados cada fin de semana?
3) Se sabe que el 40 % de las mujeres embarazadas dan a luz antes de la fecha prevista. En un hospital, han dado a luz 125 mujeres en una semana.
a) ¿Cuál es el número esperado de mujeres a las que se les retrasó el parto?
b) ¿Cuál es la probabilidad de que entre 45 y 60 mujeres se les haya adelantado el parto?
4) En las elecciones generales del país, el presidente del gobierno elegido por los ciudadanos ha recibido un 64 % de los votos favorables. Se escoge una muestra al azar de 120 votantes.
a) ¿Cuál es la distribución que sigue la proporción de votantes que han votado al presidente de la muestra?
b) Halla la probabilidad de que más del 70 % de los votantes de la muestra votasen al presidente.
5) El 2 % de las piezas que produce una máquina presenta algún tipo de irregularidad, por lo que es defectuosa. Se toma una muestra aleatoria de 60 piezas.
a) ¿Cuál es la probabilidad de que no exista ninguna pieza defectuosa?
b) Halla la probabilidad de que en la muestra existan entre 2 y 5 piezas defectuosas.
6) El responsable de la sede central de una empresa afirma que las edades de sus empleados siguen una distribución normal con una media de 41 años y una desviación típica de 5 años. Por otro lado, el responsable de una sede de las sucursales de dicha empresa en otro país, ha determinado que sus empleados también tienen edades que se ajustan a una distribución normal con una media de 39 años y desviación típica de 3 años.
Con el fin de hacer un estudio comparativo se seleccionan muestras de 40 personas de cada sede de la empresa.
a) Determina la distribución para la diferencia de las medias muestrales.
b) ¿Cuál es la probabilidad de que los empleados de la sede central tengas una media de edad de al menos 3 años mayor que los de la sucursal extranjera?
7) Las pruebas de control de calidad para un modelo A de bombilla han determinado que la duración se distribuye como una normal de media 3300 horas y desviación típica 180 horas; mientras que para otro modelo B la duración media es de 3200 horas y desviación típica 155 horas.
Si se toman muestras aleatorias de 100 bombillas de cada modelo :
a) ¿Cuáles son los parámetros de media y desviación típica de la diferencia de las medias muestrales?
b) Halla la probabilidad de que la diferencia de las medias de las duraciones de las bombillas de cada modelo sea inferior a 40 horas.
8) El peso de los huevos de gallina producidos por una granja sigue una distribución normal de media 67 gramos y desviación típica 6 gramos. En otra granja con otro tipo de alimentación se ha comprobado que el peso de los huevos corresponde a otra distribución normal de media 65 gramos y desviación típica 1 gramo.
a) Si se tomara al azar muestras de 200 huevos de cada granja, determinar la distribución para la diferencia de medias muestrales. ¿Cuál es la probabilidad de que la diferencia en los pesos de los huevos sea menor a 3 gramos?
b) Si se toma una muestra de 120 huevos de la primera granja y 150 de la segunda, ¿cuál es la probabilidad de que la diferencia en los pesos de los huevos sea 3 gramos?
9) Una empresa de telefonía móvil dota a sus teléfonos de baterías que provienen de dos fábricas distintas, A y B. Las baterías de la fábrica A duran una media de 114 horas, con una desviación típica de 23 horas, mientras que las de la fábrica B tienen una duración media de 109 horas y una desviación típica de 17 horas.
Se toma una mujestra al azar formada por 63 baterías de la fábrica A y 55 de la fábrica B.
a) ¿Cuál es la distribución de la diferencia de medias para la muestra anterior?
b) ¿Cuál es la probabilidad de que la diferencia de las medias sea mayor a 18 horas?
10) En el juzgado de una ciudad se presentaron el año pasado 8300 denuncias y este año ha habido 1100 más. Se van a seleccionar muestras aleatorias formadas por un 3 % y un 5 % de ellas, respectivamente.
Si se sabe que el tiempo dedicado el año pasado al trámite de las denuncias sigue una distribución normal con media de 8 meses y desviación típica de 3 meses, y que este año los parámetros de distribución han aumentado un 4 % cada uno, calcula la probabilidad de que la diferencia de tiempo medio invertido en los trámites judiciales de las muestras sea menor a 0,2 meses.
1) Se sabe que el 10 % de los habitantes de una determinada ciudad va regularmente al teatro. Se toma una muestra al azar de 100 habitantes de esta ciudad, ¿cuál es la probabilidad aproximada de que al menos el 13 % de ellos vaya regularmente al teatro?

2) Un estudio realizado por una compañia de seguros de automóviles establece que una de cada cinco personas accidentadas es mujer. Si se contabilizan, por término medio, 169 accidentes cada fin de semana :
a) ¿Cuál es la probabilidad de que, en un fin de semana, la proporción de mujeres accidentadas supere el 24 % ?
b) ¿Cuál es la probabilidad de que, en un fin de semana, la proporción de hombres accidentados supere el 85 % ?
c) ¿Cuál es, por término medio, el número esperado de hombres accidentados cada fin de semana?
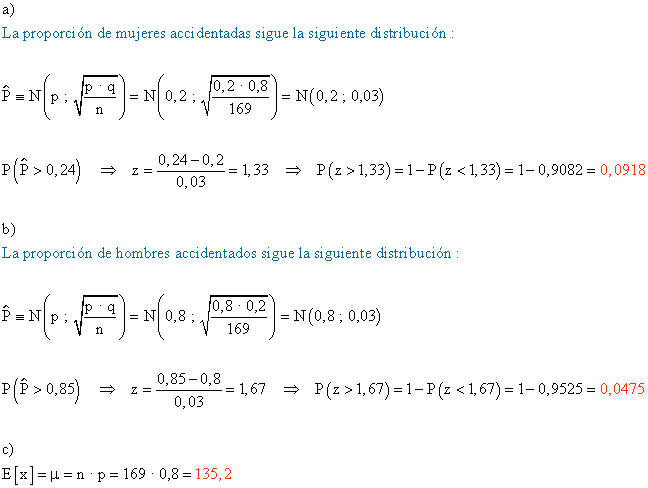
38) Se sabe que el 40 % de las mujeres embarazadas dan a luz antes de la fecha prevista. En un hospital, han dado a luz 125 mujeres en una semana.
a) ¿Cuál es el número esperado de mujeres a las que se les retrasó el parto?
b) ¿Cuál es la probabilidad de que entre 45 y 60 mujeres se les haya adelantado el parto?
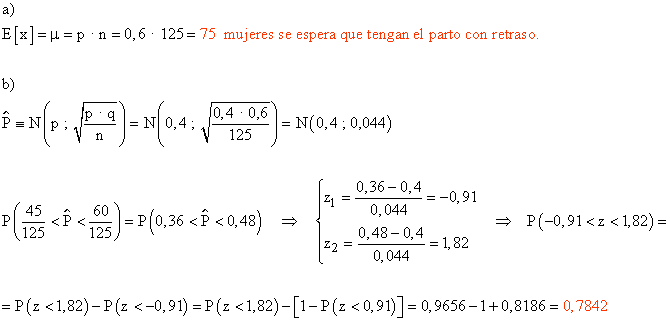
4) En las elecciones generales del país, el presidente del gobierno elegido por los ciudadanos ha recibido un 64 % de los votos favorables. Se escoge una muestra al azar de 120 votantes.
a) ¿Cuál es la distribución que sigue la proporción de votantes que han votado al presidente de la muestra?
b) Halla la probabilidad de que más del 70 % de los votantes de la muestra votasen al presidente.

5) El 2 % de las piezas que produce una máquina presenta algún tipo de irregularidad, por lo que es defectuosa. Se toma una muestra aleatoria de 60 piezas.
a) ¿Cuál es la probabilidad de que no exista ninguna pieza defectuosa?
b) Halla la probabilidad de que en la muestra existan entre 2 y 5 piezas defectuosas.
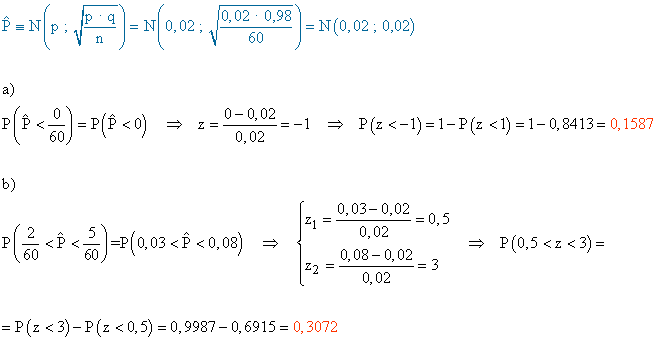
6) El responsable de la sede central de una empresa afirma que las edades de sus empleados siguen una distribución normal con una media de 41 años y una desviación típica de 5 años. Por otro lado, el responsable de una sede de las sucursales de dicha empresa en otro país, ha determinado que sus empleados también tienen edades que se ajustan a una distribución normal con una media de 39 años y desviación típica de 3 años.
Con el fin de hacer un estudio comparativo se seleccionan muestras de 40 personas de cada sede de la empresa.
a) Determina la distribución para la diferencia de las medias muestrales.
b) ¿Cuál es la probabilidad de que los empleados de la sede central tengas una media de edad de al menos 3 años mayor que los de la sucursal extranjera?
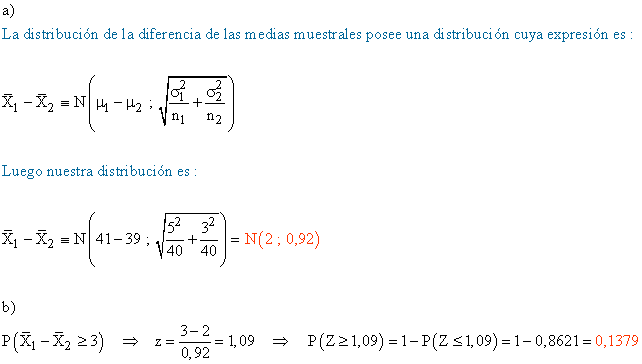
7) Las pruebas de control de calidad para un modelo A de bombilla han determinado que la duración se distribuye como una normal de media 3300 horas y desviación típica 180 horas; mientras que para otro modelo B la duración media es de 3200 horas y desviación típica 155 horas.
Si se toman muestras aleatorias de 100 bombillas de cada modelo :
a) ¿Cuáles son los parámetros de media y desviación típica de la diferencia de las medias muestrales?
b) Halla la probabilidad de que la diferencia de las medias de las duraciones de las bombillas de cada modelo sea inferior a 40 horas.

8) El peso de los huevos de gallina producidos por una granja sigue una distribución normal de media 67 gramos y desviación típica 6 gramos. En otra granja con otro tipo de alimentación se ha comprobado que el peso de los huevos corresponde a otra distribución normal de media 65 gramos y desviación típica 1 gramo.
a) Si se tomara al azar muestras de 200 huevos de cada granja, determinar la distribución para la diferencia de medias muestrales. ¿Cuál es la probabilidad de que la diferencia en los pesos de los huevos sea menor a 3 gramos?
b) Si se toma una muestra de 120 huevos de la primera granja y 150 de la segunda, ¿cuál es la probabilidad de que la diferencia en los pesos de los huevos sea 3 gramos?
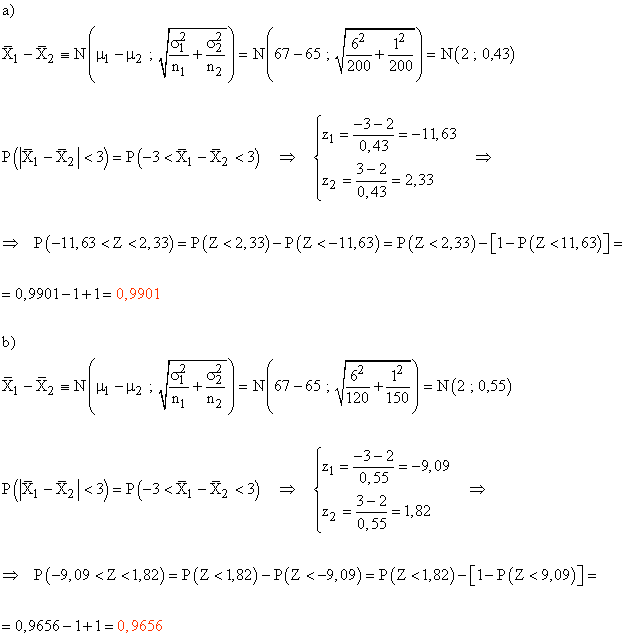
9) Una empresa de telefonía móvil dota a sus teléfonos de baterías que provienen de dos fábricas distintas, A y B. Las baterías de la fábrica A duran una media de 114 horas, con una desviación típica de 23 horas, mientras que las de la fábrica B tienen una duración media de 109 horas y una desviación típica de 17 horas.
Se toma una mujestra al azar formada por 63 baterías de la fábrica A y 55 de la fábrica B.
a) ¿Cuál es la distribución de la diferencia de medias para la muestra anterior?
b) ¿Cuál es la probabilidad de que la diferencia de las medias sea mayor a 18 horas?
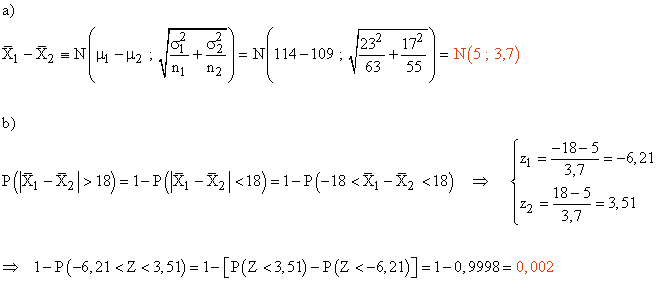
10) En el juzgado de una ciudad se presentaron el año pasado 8300 denuncias y este año ha habido 1100 más. Se van a seleccionar muestras aleatorias formadas por un 3 % y un 5 % de ellas, respectivamente.
Si se sabe que el tiempo dedicado el año pasado al trámite de las denuncias sigue una distribución normal con media de 8 meses y desviación típica de 3 meses, y que este año los parámetros de distribución han aumentado un 4 % cada uno, calcula la probabilidad de que la diferencia de tiempo medio invertido en los trámites judiciales de las muestras sea menor a 0,2 meses.



 INICIO
INICIO