Problemas resueltos de teorema central del límite.
Distribuciones en la media y distribuciones de la suma de las medias de la muestra.
1) Un dado cúbico está numerado del 1 al 6.
a) Calcula la media y la desviacion típica de la población formada por los seis números.
b) Forma todas las muestras posibles de tamaño 2 que podamos obtener con repetición de esta población.
c) Halla la media y la desviación típica de las medias muestrales.
2) De una variable aleatoria x de distribución desconocida, media 14 y desviación típica 1,7 se extraen muestras de tamaño n.
¿ Qué se puede decir de la distribución de las medias muestrales:
a) en el caso de que n = 40 ?
b) en el caso de que n = 18 ?
3) Una variable aleatoria x se distribuye según una normal N ( 110 ; 17 ). ¿Qué se puede afirmar de la distribución de las medias
de las muestras de tamaño n :
a) si n = 39 ?
b) si n = 12 ?
4) Una variable aleatoria sigue una distribución normal de paramétros μ = 17 y σ = 3. Halla las distribuciones de las medias muestrales de muestras de tamaño 15, 25, 40, 100 y 135. ¿Se podría hacer de no seguir la población una distribución normal?
5) Una población de un tipo de plantas tiene una talla media de 17 centímetros y la desviación típica es de 1,8 centímetros. Se toma al azar una muestra de 30 plantas. ¿Cuál es la probabilidad de que la media de las tallas de la muestra sea superior a 15 centímetros?
6) Un fabricante produce tabletas de chocolate cuyo peso en gramos sigue una distribución normal de media 125 gramos y desviación típica 4 gramos.
a) Si las tabletas se empaquetan en lotes de 25, ¿cuál es la probabilidad de que el peso medio de las tabletas de un lote se encuentre entre 124 y 126 gramos?
b) Si los lotes fueran de 64 tabletas, ¿cuál sería la probabilidad de que el peso medio de las tabletas del lote superase los 124 gramos?
7) El sueldo de los trabajadores de una multinacional sigue una distribución normal de media 2500 € y desviación típica 600 €.
Si se toma una muestra de 64 trabajadores :
a) ¿De qué tipo es la distribución de las medias de las muestras que pueden extraerse?
b) ¿Cuál es la probabilidad de que la media de la muestra sea menor que 2350 €?
8) Se supone que la distribución de la temperatura del cuerpo humano en la población tiene de media 37 ºC y de desviación típica 0,85 ºC.
Se elige una muestra de 105 personas y se pide :
a) Calcular la probabilidad de que la temperatura media sea menor de 36,9 ºC.
b) Calcular la probabilidad de que la temperatura media esté comprendida entre 36,5 ºC y 37,5 ºC.
9) Se sabe que las puntuaciones de un test siguen una ley normal de media 36 y desviación típica 4,8.
a) Si se toma una muestra aleatoria de 16 individuos, ¿cuál es la probabilidad de que la media de esta muestra sea superior a 35 puntos?
b) ¿Qué porcentaje de muestras de tamaño 25 tiene una media muestral comprendida entre 34 y 36?
10) Se sabe que el peso medio de los pasajeros de un avión es 76 kg, con una desviación típica de 7,4 kg. Por las normativas de seguridad, la suma de los pesos de los pasajeros no puede superar las 16 toneladas. Si la compañía aérea ha vendido 210 pasajes, ¿cuál es la probabilidad de que cumpla con la normativa de seguridad?
11) El voltaje de las baterías de un fabricante es de 12 voltios de media y con una desviación típica de 0,3 voltios. Elegimos al azar 5 de esas baterías y se conectan en seria, lo que supone que se suman los voltajes. Calcula la probabilidad de que tengan un voltaje conjunto de más de 61 voltios.
12) El peso de los inquilinos de una comunidad de vecinos sigue una distribución normal de media 67 kg y desviación típica de 6 kg. ¿Cuál es la probabilidad de que al subir 6 personas en un ascensor no superen el peso máximo permitido de 400 kg?
13) Los sueldos, en euros, de los empleados de una fábrica se distribuyen según una normal de media 1350 y desviación típica 270. Se elige al azar una muestra de 40 de ellos. ¿Cuál es la probabilidad de que la suma de sus sueldos sea superior a 55000 euros?
14) En una urna hay seis bolas numeradas del 1 al 6. Calcula la distribución que siguen las sumas muestrales de tamaño 15 y 40, extrayendo todas las bolas con reemplazamiento. En este último caso, halla la probabilidad de que la suma de las puntuaciones sea menor a 145.
1) Un dado cúbico está numerado del 1 al 6.
a) Calcula la media y la desviacion típica de la población formada por los seis números.
b) Forma todas las muestras posibles de tamaño 2 que podamos obtener con repetición de esta población.
c) Halla la media y la desviación típica de las medias muestrales.
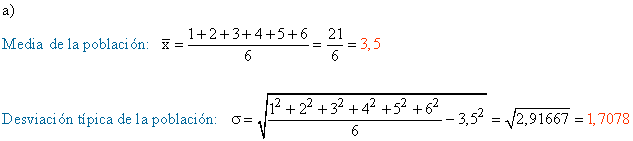
b)
Muestras posibles de tamaño 2 :
{ 1, 1 }, { 1, 2 }, { 1, 3 }, { 1, 4 }, { 1, 5 }, { 1, 6 }, { 2, 1 }, { 2, 2 }, { 2, 3 }, { 2, 4 }, { 2, 5 }, { 2, 6 }, { 3, 1 }, { 3, 2 }, { 3, 3 }, { 3, 4 }, { 3, 5 }, { 3, 6 }, { 4, 1 }, { 4, 2 }, { 4, 3 }, { 4, 4 }, { 4, 5 }, { 4, 6 }, { 5, 1 }, { 5, 2 }, { 5, 3 }, { 5, 4 }, { 5, 5 }, { 5, 6 }, { 6, 1 }, { 6, 2 }, { 6, 3 }, { 6, 4 }, { 6, 5 }, { 6, 6 }
c)
Medias muestrales : { 1 ; 1,5 ; 2 ; 2,5 ; 3 ; 3,5 ; 4 ; 4,5 ; 5 ; 5,5 ; 6 }
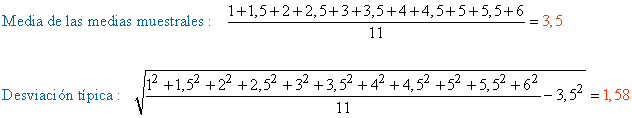
2) De una variable aleatoria x de distribución desconocida, media 14 y desviación típica 1,7 se extraen muestras de tamaño n.
¿ Qué se puede decir de la distribución de las medias muestrales:
a) en el caso de que n = 40 ?
b) en el caso de que n = 18 ?

3) Una variable aleatoria x se distribuye según una normal N ( 110 ; 17 ). ¿Qué se puede afirmar de la distribución de las medias
de las muestras de tamaño n :
a) si n = 39 ?
b) si n = 12 ?

4) Una variable aleatoria sigue una distribución normal de paramétros μ = 17 y σ = 3. Halla las distribuciones de las medias muestrales de muestras de tamaño 15, 25, 40, 100 y 135. ¿Se podría hacer de no seguir la población una distribución normal?

5) Una población de un tipo de plantas tiene una talla media de 17 centímetros y la desviación típica es de 1,8 centímetros. Se toma al azar una muestra de 30 plantas. ¿Cuál es la probabilidad de que la media de las tallas de la muestra sea superior a 15 centímetros?

6) Un fabricante produce tabletas de chocolate cuyo peso en gramos sigue una distribución normal de media 125 gramos y desviación típica 4 gramos.
a) Si las tabletas se empaquetan en lotes de 25, ¿cuál es la probabilidad de que el peso medio de las tabletas de un lote se encuentre entre 124 y 126 gramos?
b) Si los lotes fueran de 64 tabletas, ¿cuál sería la probabilidad de que el peso medio de las tabletas del lote superase los 124 gramos?
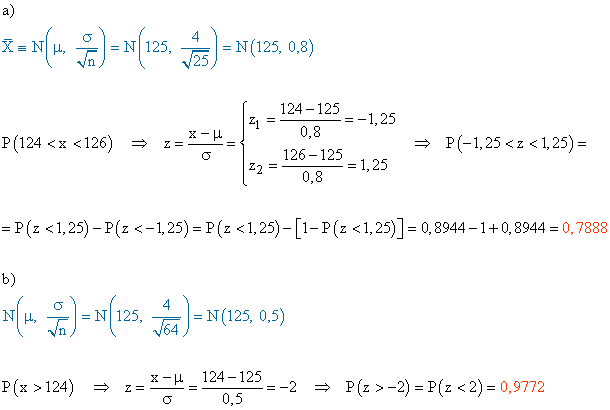
7) El sueldo de los trabajadores de una multinacional sigue una distribución normal de media 2500 € y desviación típica 600 €.
Si se toma una muestra de 64 trabajadores :
a) ¿De qué tipo es la distribución de las medias de las muestras que pueden extraerse?
b) ¿Cuál es la probabilidad de que la media de la muestra sea menor que 2350 €?

8) Se supone que la distribución de la temperatura del cuerpo humano en la población tiene de media 37 ºC y de desviación típica 0,85 ºC.
Se elige una muestra de 105 personas y se pide :
a) Calcular la probabilidad de que la temperatura media sea menor de 36,9 ºC.
b) Calcular la probabilidad de que la temperatura media esté comprendida entre 36,5 ºC y 37,5 ºC.
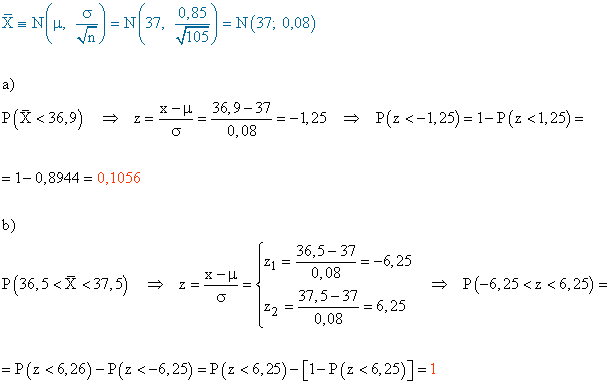
9) Se sabe que las puntuaciones de un test siguen una ley normal de media 36 y desviación típica 4,8.
a) Si se toma una muestra aleatoria de 16 individuos, ¿cuál es la probabilidad de que la media de esta muestra sea superior a 35 puntos?
b) ¿Qué porcentaje de muestras de tamaño 25 tiene una media muestral comprendida entre 34 y 36?
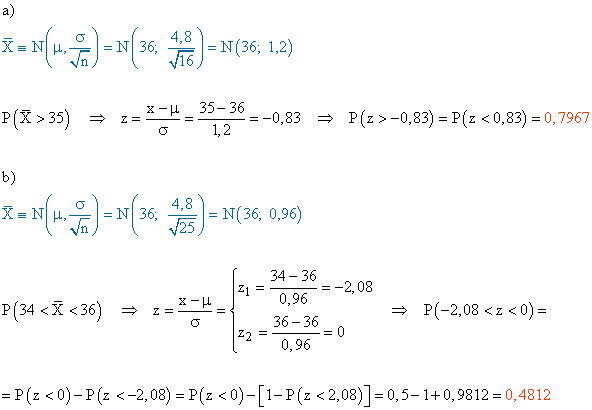
10) Se sabe que el peso medio de los pasajeros de un avión es 76 kg, con una desviación típica de 7,4 kg. Por las normativas de seguridad, la suma de los pesos de los pasajeros no puede superar las 16 toneladas. Si la compañía aérea ha vendido 210 pasajes, ¿cuál es la probabilidad de que cumpla con la normativa de seguridad?
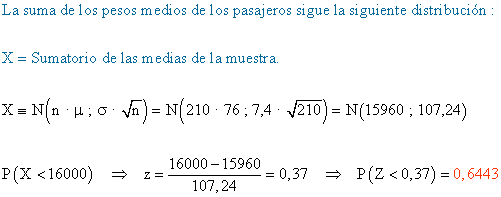
11) El voltaje de las baterías de un fabricante es de 12 voltios de media y con una desviación típica de 0,3 voltios. Elegimos al azar 5 de esas baterías y se conectan en seria, lo que supone que se suman los voltajes. Calcula la probabilidad de que tengan un voltaje conjunto de más de 61 voltios.

12) El peso de los inquilinos de una comunidad de vecinos sigue una distribución normal de media 67 kg y desviación típica de 6 kg. ¿Cuál es la probabilidad de que al subir 6 personas en un ascensor no superen el peso máximo permitido de 400 kg?

13) Los sueldos, en euros, de los empleados de una fábrica se distribuyen según una normal de media 1350 y desviación típica 270. Se elige al azar una muestra de 40 de ellos. ¿Cuál es la probabilidad de que la suma de sus sueldos sea superior a 56500 euros?

14) En una urna hay seis bolas numeradas del 1 al 6. Calcula la distribución que siguen las sumas muestrales de tamaño 15 y 40, extrayendo todas las bolas con reemplazamiento. En este último caso, halla la probabilidad de que la suma de las puntuaciones sea menor a 145.



 INICIO
INICIO