Distribución en el muestreo de medias: distribución de la media.

Teorema central del límite

Dada una población de media μ y desviación típica σ, no necesariamente normal. La distribución del las medias de las muestras de tamaño n:

Tiene la misma media μ que la población.
Su desviación típica es 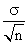y , por tanto, disminuye al aumentar n.
A partir de 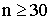es prácticamente normal.

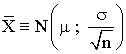
Las distribuciones de las medias muestrales será una normal si la distribución de partida es
normal, independientemente del tamaño de la muestra.
Si la distribución de partida no es normal, el tamaño de la muestra debe ser superior o igual a 30.

Ejemplo 1:

De una variable aleatoria x de distribución desconocida , media 14 y desviación típica 1,7 se extraen muestras de tamaño n. ¿ Qué se puede decir de la distribución de las medias muestrales :
a) en el caso de que n = 40 ?
b) en el caso de que n = 18 ?

Ejemplo 2:

Una variable aleatoria x se distribuye según una normal N ( 110 ; 17 ). ¿Qué se puede afirmar de la distribución de las medias de las muestras de tamaño n :
a) si n = 39 ?
b) si n = 12 ?

Consecuencias del teorema central del límite

1. Control de las medias muestrales

En una población de media μ y desviación típica σ , vamos a extraer una muestra de tamaño n. Sabemos que la distribución de las medias ,

, de todas las posibles muestras es

. Por tanto se puede averiguar la probabilidad de que la media de una muestra concreta esté en un cierto intervalo.

Ejemplo 3 : distribución de la media de una muestra.

Una población de un tipo de plantas tiene una talla media de 17 centímetros y la desviación típica es de 1,8 centímetros. Se toma al azar una muestra de 30 plantas. ¿Cuál es la probabilidad de que la media de las tallas de la muestra sea superior a 15 centímetros?

Ejemplo 4 : distribución de la media de una muestra.

Se sabe que las puntuaciones de un test siguen una ley normal de media 36 y desviación típica 4,8. a) Si se toma una muestra aleatoria de 16 individuos, ¿cuál es la probabilidad de que la media de esta muestra sea superior a 35 puntos? b) ¿Qué porcentaje de muestras de tamaño 25 tiene una media muestral comprendida entre 34 y 36?

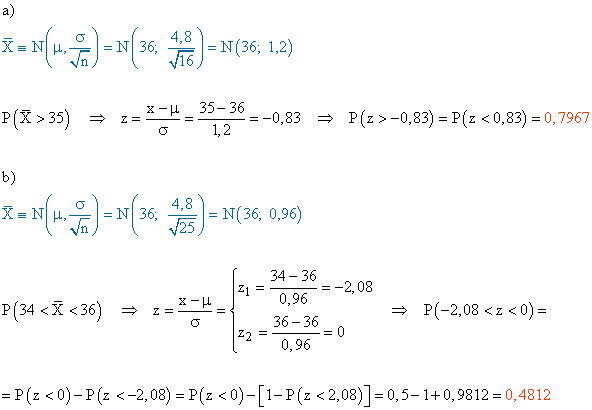
2. Control de la suma de todos los individuos de la muestra

Si tomamos una muestra aleatoria simple de tamaño n de una variable aleatoria X: X₁, X₂, ..., X_n con media μ y desviación típica σ , entonces la variable aleatoria X = X₁ + X₂+ ... + X_n para n suficientemente grande () la distribución muestral de medias X se aproxima a una distribución normal:

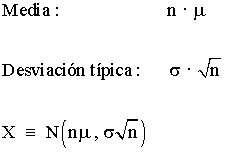
Ejemplo 5 : distribución de la suma de las medias.

Se sabe que el peso medio de los pasajeros de un avión es 76 kg, con una desviación típica de 7,4 kg. Por las normativas de seguridad, la suma de los pesos de los pasajeros no puede superar las 16 toneladas. Si la compañía aérea ha vendido 210 pasajes, ¿cuál es la probabilidad de que cumpla con la normativa de seguridad?

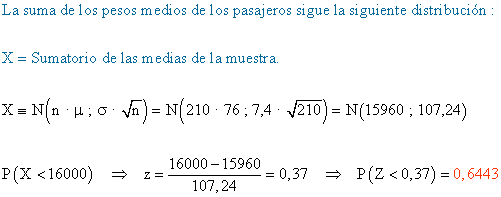
Ejemplo 6 : distribución de la suma de las medias.

El voltaje de las baterías de un fabricante es de 12 voltios de media y con una desviación típica de 0,3 voltios. Elegimos al azar 5 de esas baterías y se conectan en seria, lo que supone que se suman los voltajes. Calcula la probabilidad de que tengan un voltaje conjunto de más de 61 voltios.

3. Inferir la media de una población a partir de una muestra.

Esta es la aplicación más importante del teorema y a partir de una muestra se pueden extraer conclusiones válidas sobre la media de la población.

Este apartado se verá en los temas siguientes de intervalos de confienza y contraste de hipótesis.