Problemas resueltos de aproximación de una binomial a la normal.
1) Se lanza un dado 720 veces. Calcula la probabilidad aproximada de que salgan, al menos, 110 seises.
2) Tiramos una moneda perfecta 100 veces. Hacemos la predicción de que saldrá un número de caras comprendido entre 40 y 53. Calcula la probabilidad de acertar.
3) Se ha realizado una encuesta sobre una población en la que solo el 15 % ha leído más de tres libros. Elegida al azar una muestra de 60 personas, calcula la probabilidad de que:
a) Más de cinco personas hayan leído más de tres libros.
b) Como máximo haya seis personas que han leído más de tres libros.
4) Se sabe que dos de cada ocho habitantes de una ciudad utiliza el transporte público para ir a su trabajo. Se hace una encuesta a 140 de esos ciudadanos. Determinar:
a) Número esperado de ciudadanos que no van a su trabajo en transporte público.
b) Probabilidad de que el número de ciudadanos que van al trabajo en transporte público esté entre 30 y 45.
5) En un centro comercial el 35 % de los clientes paga con tarjeta.
a) Si en una caja han pagado 120 clientes, ¿cuántos de ellos se espera que lo hayan hecho con tarjeta?
b) Si en una caja han pagado 200 clientes, ¿cuál es la probabilidad de que lo hayan hecho con tarjeta entre 60 y 85 de ellos?
c) Si en una caja han pagado 400 clientes, ¿cuál es la probabilidazd de que al menos 260 no lo hayan hecho con tarjeta?
6) El 90 % de los miembros de un club pasan sus vacaciones en la playa. Calcule una aproximación, obtenida utilizando la tabla normal, de la probabilidad de que, en un grupo de 60 miembros, 50 o menos vayan a ir a la playa a pasar sus vacaciones.
7) Tenemos un bombo de lotería con 10 bolas idénticas numeradas del 1 al 10.
a) Hacemos seis extracciones consecutivas de una bola que se devuelve al bombo después de cada extracción. Calcula la probabilidad de que el número cuatro salga, como máximo, una vez en estas extracciones.
b) Si hacemos 150 extracciones como en el apartado anterior, ¿cuál es la probabilidad de que el número cinco salga como máximo 16 veces?
8) El 25 % de las viviendas de una región tiene conexión a internet. Se eligen 80 viviendas y se pide :
a) La probabilidad de que al menos 20 de ellas estén conectadas a internet.
b) El número esperado de viviendas no conectadas a internet.
c) La probabilidad de que el número de viviendas con internet esté entre 10 y 30.
9) La probabilidad de que deje de fumar un paciente, que se ha sometido a un régimen médico riguroso, es de 0,8. Se eligen 100 pacientes, que se han sometido a dicho régimen. ¿Cuál es la probabilidad de que hayan dejado de fumar entre 74 y 85 pacientes, ambos inclusive?
10) Tenemos una moneda trucada cuya probabilidad de cara es de 1 / 3 y cuya probabilidad de cruz es de 2 / 3. Antes de tirar 120 veces la moneda hacemos la predicción de que el número de caras que saldrá estará entre 35 y 45, ambos inclusive. Calcula la probabilidad de no acertar la predicción.
11) Explica en qué casos puedes utilizar la distribución normal para calcular de forma aproximada probabilidades de distribución binomiales.
El 10 % de los artículos fabricados en una empresa de material cerámico tiene algún defecto. Obtén ( utilizando la aproximación citada, si lo consideras conveniente ) la probabilidad de que :
a) En un lote de 10 artículos se encuentre al menos uno defectuoso.
b) En un lote de 100 artículos hayan al menos 10 defectuosos.
12) Se supone que los resultados de un examen siguen una distribución normal con media 78 y varianza 36. Se pide :
a) ¿Cuál es la probabilidad de que una persona que se presente al examen obtenga una calificación superior a 72?
b) Suponga que a los estudiantes que se encuentran en el 10 % de la parte superior de la distribución se les asigna una calificación A ( A significa " excelente " ). ¿Cuál es la puntuación mínima que debe alcanzar un estudiante para recibir la calificación A?
c) Calcular la proporción de estudiantes que tienen puntuaciones que exceden por lo menos en 5 puntos de la puntuación que marca la frontera entre el Apto y el No-Apto ( son declarados No-Aptos el 25 % de los estudiantes que obtuvieron las puntuaciones más bajas).
d) Si se sabe que la calificación de un estudiante es mayor que 72, ¿cuál es la probabilidad de que su calificación sea, de hecho, superior a 84?
1) Se lanza un dado 720 veces. Calcula la probabilidad aproximada de que salgan, al menos, 110 seises.

2) Tiramos una moneda perfecta 100 veces. Hacemos la predicción de que saldrá un número de caras comprendido entre 40 y 53. Calcula la probabilidad de acertar.

3) Se ha realizado una encuesta sobre una población en la que solo el 15 % ha leído más de tres libros. Elegida al azar una muestra de 60 personas, calcula la probabilidad de que:
a) Más de cinco personas hayan leído más de tres libros.
b) Como máximo haya seis personas que han leído más de tres libros.
Tenemos una distribución binomial B ( 50 ; 0,15 ), siendo X la variable que expresa el número de personas que han leído más de tres libros. Como el número de datos es muy grande y se verifica que n · p = 7,5 ≥5 y
n · q = 42,5 ≥ 5, aproximaremos mediante una distribución normal de parámetros :
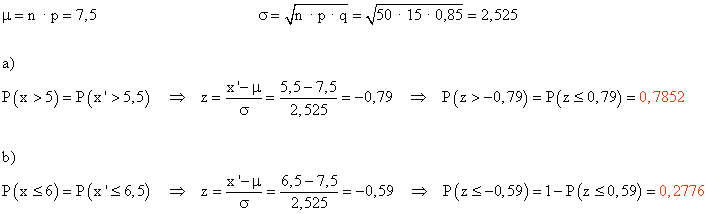
4) Se sabe que dos de cada ocho habitantes de una ciudad utiliza el transporte público para ir a su trabajo. Se hace una encuesta a 140 de esos ciudadanos. Determinar:
a) Número esperado de ciudadanos que no van a su trabajo en transporte público.
b) Probabilidad de que el número de ciudadanos que van al trabajo en transporte público esté entre 30 y 45.

5) En un centro comercial el 35 % de los clientes paga con tarjeta.
a) Si en una caja han pagado 120 clientes, ¿cuántos de ellos se espera que lo hayan hecho con tarjeta?
b) Si en una caja han pagado 200 clientes, ¿cuál es la probabilidad de que lo hayan hecho con tarjeta entre 60 y 85 de ellos?
c) Si en una caja han pagado 400 clientes, ¿cuál es la probabilidazd de que al menos 260 no lo hayan hecho con tarjeta?

6) El 90 % de los miembros de un club pasan sus vacaciones en la playa. Calcule una aproximación, obtenida utilizando la tabla normal, de la probabilidad de que, en un grupo de 60 miembros, 50 o menos vayan a ir a la playa a pasar sus vacaciones.

7) Tenemos un bombo de lotería con 10 bolas idénticas numeradas del 1 al 10.
a) Hacemos seis extracciones consecutivas de una bola que se devuelve al bombo después de cada extracción. Calcula la probabilidad de que el número cuatro salga, como máximo, una vez en estas extracciones.
b) Si hacemos 150 extracciones como en el apartado anterior, ¿cuál es la probabilidad de que el número cinco salga como máximo 16 veces?
a)
Sea X la variable aleatoria que describe el número de veces que sal el número 4. Se trata de una B ( 6 ; 0,1 ) y la probabilidad pedida es la siguiente :
![]()
b)
Consideramos ahora que la variable X describe el número de veces que sale el número 5. Se trata así de una distribución N ( 150 ; 0,1 ). Como n · p = 15 ≥ 5 y n · q = 135 ≥ 5 podemos aproximar nuestra distribución a una normal de parámetros :
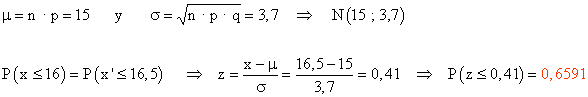
8) El 25 % de las viviendas de una región tiene conexión a internet. Se eligen 80 viviendas y se pide :
a) La probabilidad de que al menos 20 de ellas estén conectadas a internet.
b) El número esperado de viviendas no conectadas a internet.
c) La probabilidad de que el número de viviendas con internet esté entre 10 y 30.
La variable X = " número de viviendas con internet " sigue una distribución binomial B ( 80 ; 0,25 ).
Como n · p = 80 · 0,25 = 20 > 5 y n · q = 80 · 0,75 = 60 > 5, se puede aproximar X por una normal N ( 20 ; 3,87 ).
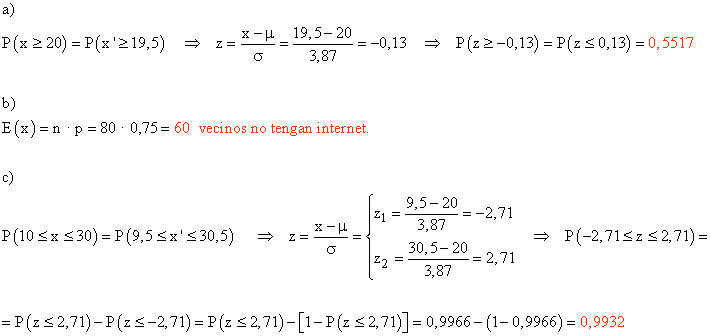
9) La probabilidad de que deje de fumar un paciente, que se ha sometido a un régimen médico riguroso, es de 0,8. Se eligen 100 pacientes, que se han sometido a dicho régimen. ¿Cuál es la probabilidad de que hayan dejado de fumar entre 74 y 85 pacientes, ambos inclusive?
X = " número de pacientes que deja de fumar "
p = 0,8 → q = 1 - p = 0,2
n = " número de pacientes que se ha sometido a dicho régimen " = 100
Tenemos una distribución binomial B ( 100 ; 0,8 ).
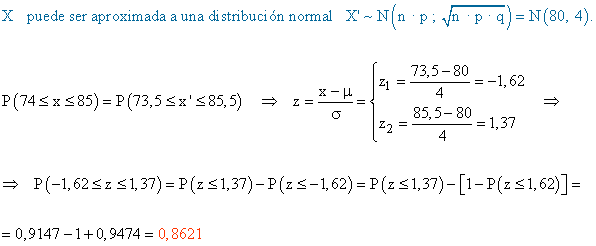
10) Tenemos una moneda trucada cuya probabilidad de cara es de 1 / 3 y cuya probabilidad de cruz es de 2 / 3. Antes de tirar 120 veces la moneda hacemos la predicción de que el número de caras que saldrá estará entre 35 y 45, ambos inclusive. Calcula la probabilidad de no acertar la predicción.
Consideramos la variable X, que indica el número de caras que salen en los 120 lanzamientos de la moneda. X es, por tanto, una distribución binomial de parámetros n = 120 y p = 1 / 3.
Como n es grande, n · p = 40 > 5 y n · q = 80 > 5, X se puede aproximar a una distribución normal de parámetros siguientes:
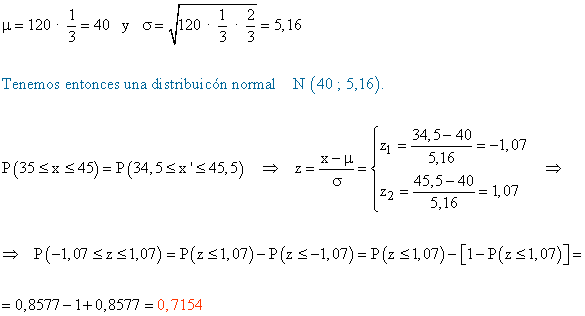
11) Explica en qué casos puedes utilizar la distribución normal para calcular de forma aproximada probabilidades de distribución binomiales.
El 10 % de los artículos fabricados en una empresa de material cerámico tiene algún defecto. Obtén ( utilizando la aproximación citada, si lo consideras conveniente ) la probabilidad de que :
a) En un lote de 10 artículos se encuentre al menos uno defectuoso.
b) En un lote de 100 artículos hayan al menos 10 defectuosos.
La distribución binomial B ( n, p ) se puede aproximar a una distribución normal N ( μ, σ ) en el caso donde n es grande y ni p ni q son próximos a cero. La aproximación será por tanto mejor cuanto mayor sea n. Se puede considerar que la aproximación es buena si n > 30 y p toma valores próximos a 0,5. También se suele considerar que la aproximación es buena si n · p y n · q son iguales o superiores a 5.
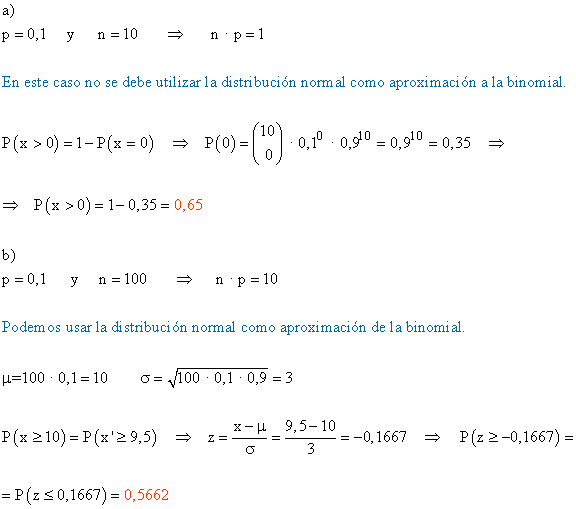
12) Se supone que los resultados de un examen siguen una distribución normal con media 78 y varianza 36. Se pide :
a) ¿Cuál es la probabilidad de que una persona que se presente al examen obtenga una calificación superior a 72?
b) Suponga que a los estudiantes que se encuentran en el 10 % de la parte superior de la distribución se les asigna una calificación A ( A significa " excelente " ). ¿Cuál es la puntuación mínima que debe alcanzar un estudiante para recibir la calificación A?
c) Calcular la proporción de estudiantes que tienen puntuaciones que exceden por lo menos en 5 puntos de la puntuación que marca la frontera entre el Apto y el No-Apto ( son declarados No-Aptos el 25 % de los estudiantes que obtuvieron las puntuaciones más bajas).
d) Si se sabe que la calificación de un estudiante es mayor que 72, ¿cuál es la probabilidad de que su calificación sea, de hecho, superior a 84?
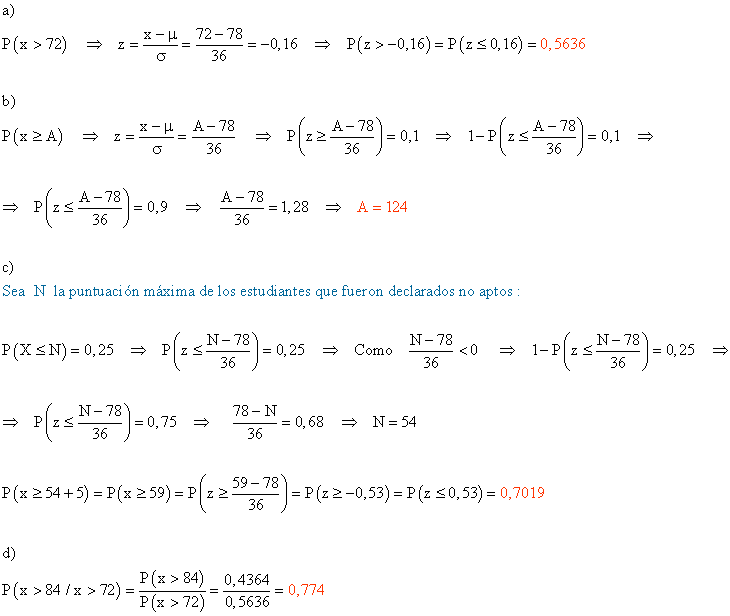


 INICIO
INICIO