Área e integral definida de una función simétrica par o impar
Función par
Si f(x) es una función simétrica par y es continua en el intervalo [-c, c] , entre x = - c y x = c :
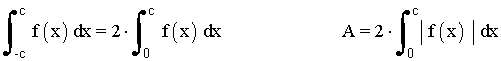
Si f es par, f( -x ) = f( x )
Ejemplo del cálculo del área de una función par:
1) Dada la siguiente función:
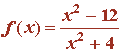
calcular el área de la región acotada encerrada por su gráfica y el eje OX.
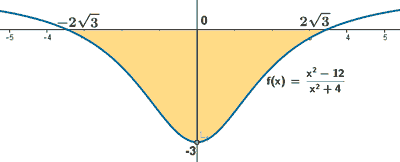
Para calcular el área de una región es útil hacer, cuando es posible, un esbozo de dicha región. Vamos pues a estudiar la función f para hacer dicho esbozo.
Puntos de corte:
Si x=0
![]()
Si y=0
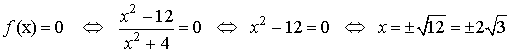
Máximos y mínimos:
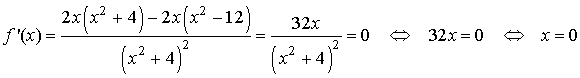
El crecimiento de la función se estudia en la siguiente tabla
| (-∞ , 0) | (0 ,∞ ) | |
|---|---|---|
| y' | y' < 0 decreciente |
y' > 0 creciente |
Y el mínimo de la función se encuentra en x = 0.
Si observamos la gráfica, el área que nos piden está delimitada desde x = -2√3 hasta x = 2√3 . Por lo que tendremos que calcular una integral definida en dicho intervalo. El área del recinto es la integral de la diferencia entre ambas funciones, es decir, de la función que "está arriba", el eje OX , menos la función que "está abajo".
Simetría:
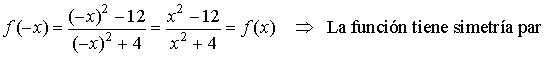
Teniendo en cuenta la simetría de la función y que es negativa:
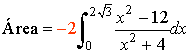
El signo menos se debe a que la función queda por debajo del eje OX, tambien se puede poner la función en valor absoluto.Y el 2 por la simetria par.
Haciendo la división de polinomios:
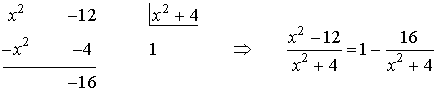
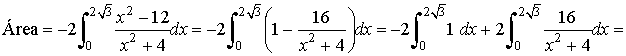
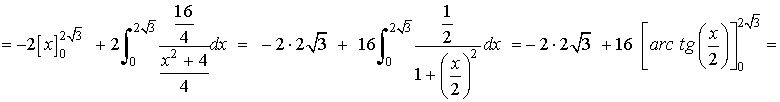
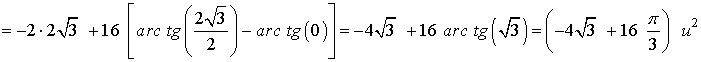
2) Calcula el área comprendida entre la curva:
![]()
el eje OX y las rectas verticales que pasan por los puntos de inflexión de dicha curva.
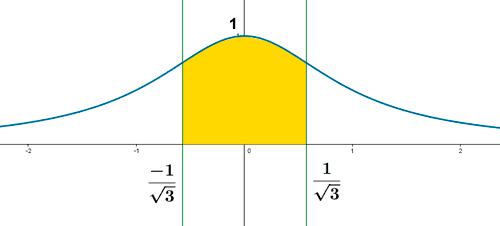
Empezamos calculando los puntos de inflexión. Dichos puntos serán aquellos que verifiquen que la segunda derivada en los mismos es nula.
Observamos ahora que la función es par:

Demostramos que la función es simétrica par:
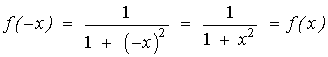
De manera que el área que nos piden puede calcularse como el doble por tener simetría par:
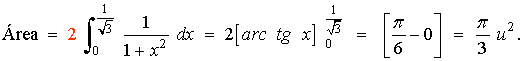
Función impar
Si f(x) es una función simétrica impar y es continua en el intervalo [-c, c] , entre x = - c y x = c :

Si f es impar, f( -x ) = - f( x )
Ejemplo del cálculo del área de una función impar:
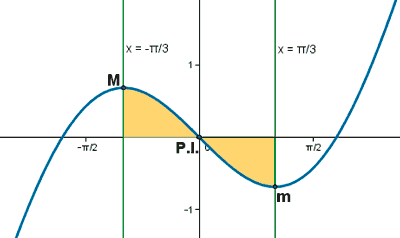
Calcula el área del recinto limitado por la curva y = x - 2 sen x y las rectas y = 0 , x = -π/3 , x = π/3 .
La función es simétrica impar:
![]()
Por lo tanto, el área entre las rectas x = -π/3 y x = π/3 es el doble del área entre las rectas x = - π/3 y x = 0
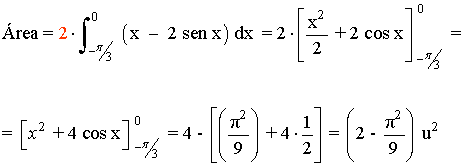
Otra forma de calcular el área
Si observamos la gráfica, el área que nos piden está delimitada desde x = -π/3 hasta x = π/3 , y está dividida en dos trozos, por lo que tendremos que calcular dos integrales.
El área de cada trozo es la integral de la diferencia entre ambas funciones, es decir, de la función que "está arriba" menos la función que "está abajo".
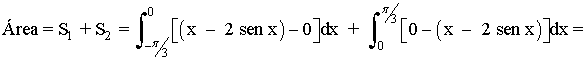
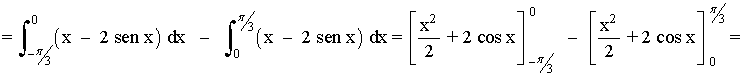
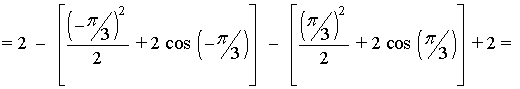
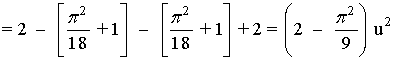


 INICIO
INICIO

