Problemas resueltos de áreas II
1) Sea f: IR → IR la función definida por
![]()
(a) Halla la ecuación de la recta tangente a la gráfica de f en un punto de la misma de ordenada y=1, teniendo en cuenta que dicha recta tangente tiene pendiente negativa.
(b) Calcula el área de la región del plano limitada por la gráfica de f, la recta tangente obtenida y el eje de ordenadas.
2) Halla el área del recinto limitado por la gráfica de la función f(x) = sen(x) y las rectas tangentes a dicha gráfica en los puntos de abscisas x = 0 y x = π
3) Calcula el área limitada por la gráfica de la función f(x) = ln x y la recta tangente a dicha gráfica en el punto x = e.
4) Calcula el área limitada por la recta y = 0, la recta x = 1 y la curva
![]()
Previamente haz un esquema del recinto cuya área hay que calcular.
5) Hallar el área limitada por el eje de abscisas, la recta x = a y la curva
![]()
siendo a la abscisa del punto máximo de la curva.
6) Halla el área limitada por la gráfica de la función f(x) = ln(1+x2) y el eje X en el intervalo [0 , 2]
7) Calcula el área de las dos partes en que la parábola y2 = 2x divide al círculo x2 + y2 = 8
8) Calcular el área de la figura plana situada en el primer cuadrante y limitada por las curvas x2 + y2 = 4x y y2 = 2x
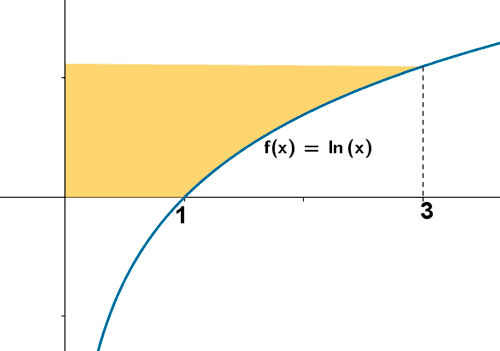
9) Siendo Ln x el logaritmo neperiano de x, halla el área de la superficie sombreada
10) Calcula el área comprendida entre la curva:
el eje OX y las rectas verticales que pasan por los puntos de inflexión de dicha curva.
11) Calcula el área del recinto acotado que está limitado por la recta y = 2x y por las curvas:

1) Sea f: IR → IR la función definida por
![]()
(a) Halla la ecuación de la recta tangente a la gráfica de f en un punto de la misma de ordenada y=1, teniendo en cuenta que dicha recta tangente tiene pendiente negativa.
(b) Calcula el área de la región del plano limitada por la gráfica de f, la recta tangente obtenida y el eje de ordenadas.
a)
Empezmos por buscar los puntos de abscisas para los cuales la ordenada es y=1. Para esto resolveremos la ecuación f(x)=1:
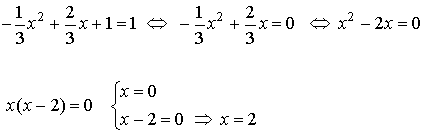
De manera que obtenemos que dichos puntos son x = 0 y x = 2.
Calculamos la derivada de f y obtenemos que
![]()
de manera que
![]()
por lo cual el punto con el que nos quedamos es x=2 y la recta que nos pide el enunciado es la dada por la ecuación
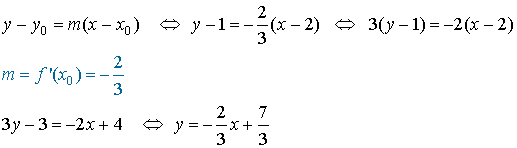
b)
Para hacer el esbozo de la gráfica hacemos un pequeño estudio de la función f:
Puntos de corte:
Para x=0, f(0)=1 de manera que el punto de corte es (0,1)
Para y=0
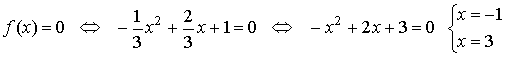
de manera que los puntos de corte son (-1,0) y (3,0).
Máximo:
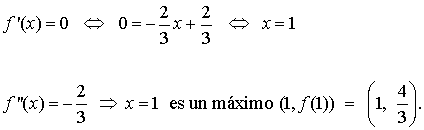
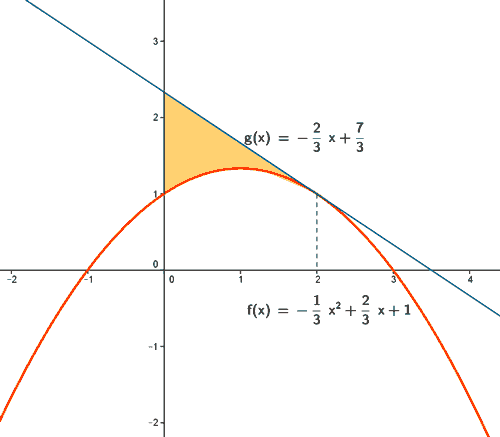
A la vista de la gráfica estamos en disposición de calcular el área pedida:
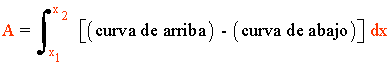
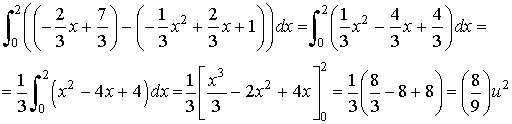
2) Halla el área del recinto limitado por la gráfica de la función f(x) = sen(x) y las rectas tangentes a dicha gráfica en los puntos de abscisas x = 0 y x = π
Empezmos por hallar las rectas tangentes a la gráfica:
Recordamos que la recta tangente viene dada por la fórmula:
y - y0 = m ( x - x0 ) donde m = f ' (x0)
f ' (x) = cos(x).
Para x=0:
f(0) = sen(0) = 0 f'(0) = cos(0) = 1
de manera que la recta tangente es:
y-0 = 1(x-0) ⇒ y=x
Para x=π:
f(π) = sen(π) = 0 f'(π) = cos(π) = -1
y la recta tangente es:
y-0 = -(x-π) ⇒ y=-x+π
Representación gráfica de la función:
Punto de corte de las dos rectas tangentes:
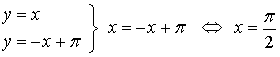
Puntos de corte de la función seno con las rectas tangentes:
sen x = 0 ⇒ x = 0, x = π
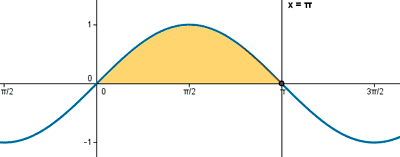
En el intervalo [0,π] la gráfica es simétrica respecto respecto a π/2, de manera que
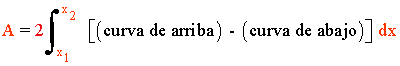
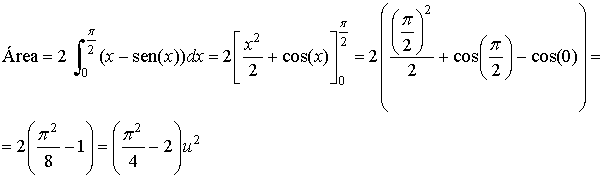
3) Calcula el área limitada por la gráfica de la función f(x) = ln x y la recta tangente a dicha gráfica en el punto x = e.
Empezamos por calcular la recta tangente a f(x) = ln x en el punto de abscisa e.
Recordamos que la recta tangente viene dada por la fórmula:
y - y0 = m ( x - x0 ) donde m = f ' (x0)
![]()
Para x = e
![]()
y la recta tangente es
![]()
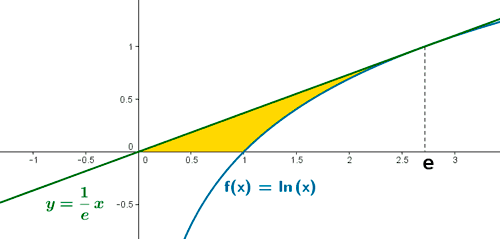
A la vista de la gráfica
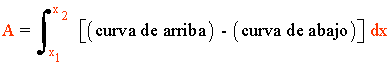
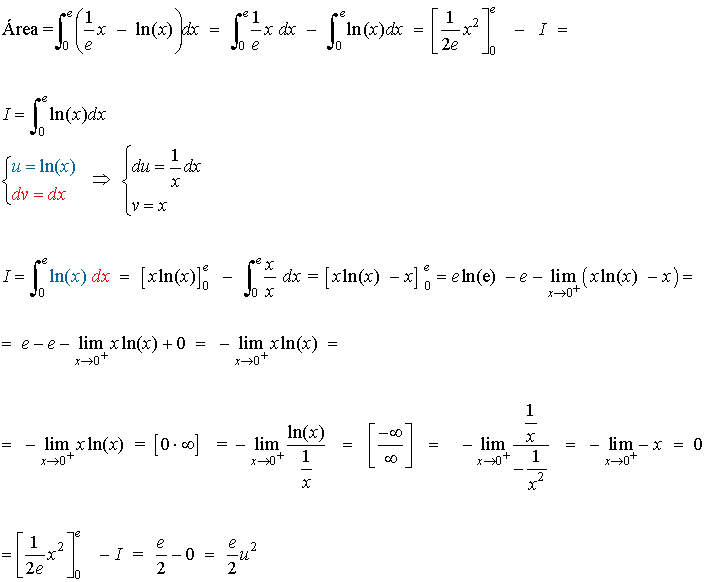
4) Calcula el área limitada por la recta y = 0, la recta x = 1 y la curva
![]()
Previamente haz un esquema del recinto cuya área hay que calcular.
Puntos de corte
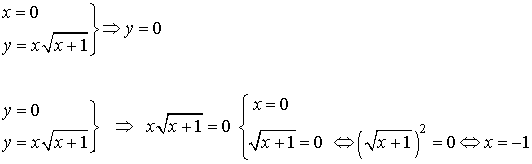
Gráfica de la función
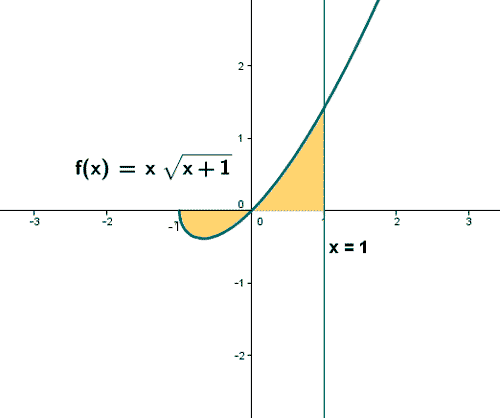
A la vista de los puntos de corte y de la gráfica estamos en disposición de hallar el área pedida:
El signo menos se debe a que la función queda por debajo del eje OX, tambien se puede poner la función en valor absoluto.
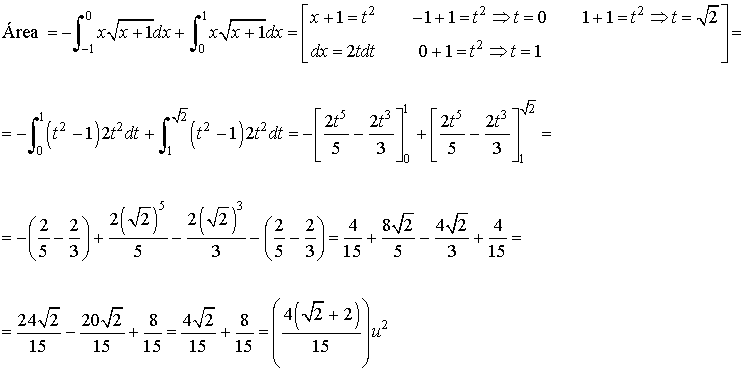
5) Hallar el área limitada por el eje de abscisas, la recta x = a y la curva
![]()
siendo a la abscisa del punto máximo de la curva.
Máximo y mínimo
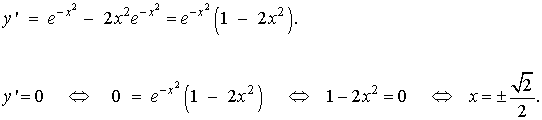
Estudiamos el signo de la primera derivada
| Intervalo | (-∞ , - √2/2) | ( - √2/2 , √2/2) | ( √2/2 , +∞) |
|---|---|---|---|
| Punto de prueba | f ' (-1) > 0 | f'(0)=1>0 | f ' (1) > 0 |
| Signo de f ' (x) | - | + | - |
| Monotonía | Decrece | Crece | Decrece |
Por tanto el máximo se alcanza en la abscisa √2/2 ya que en dicho valor de x la función pasa de crecer a decrecer.
El míximo se alcanza en la abscisa -√2/2 ya que en dicho valor de x la función pasa de decrecer a crecer.
Punto de corte con los ejes
![]()
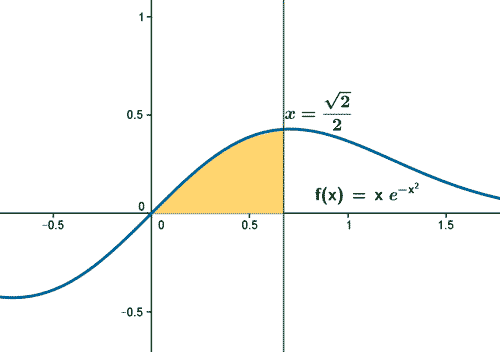
A la vista de la gráfica nos resulta más fácil calcular el área indicada. De no hacer la gráfica tomaríamos el valor absoluto de la integral, ya que un área negativa no tiene sentido.
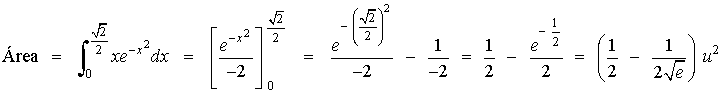
6) Halla el área limitada por la gráfica de la función f(x) = ln(1+x2) y el eje X en el intervalo [0 , 2]
Puntos de corte
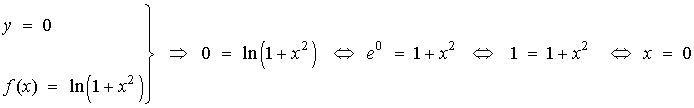
f(x) ≥ 0 para todo x ∈ [ 0 , 2 ]:
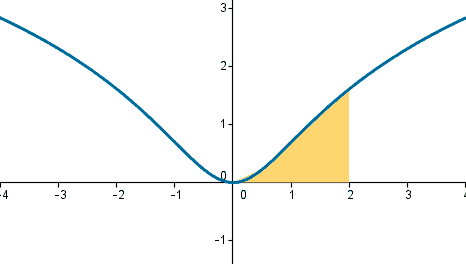
Por tanto basta con integrar en el intervalo [ 0 , 2 ]
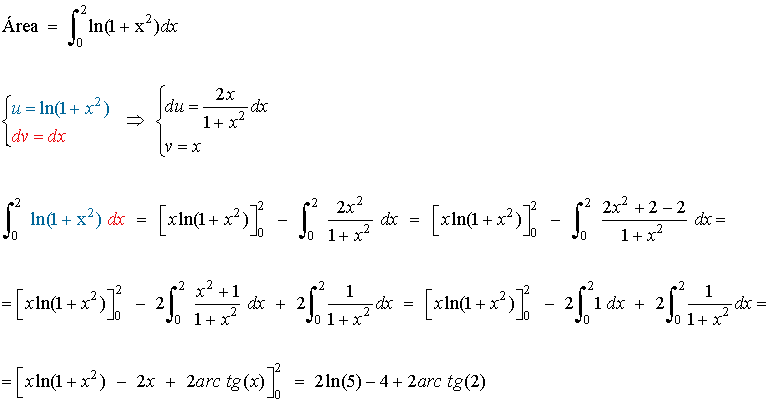
7) Calcula el área de las dos partes en que la parábola y2 = 2x divide al círculo x2 + y2 = 8
Empezamos calculando los puntos de intersección de la parábola y el círculo.
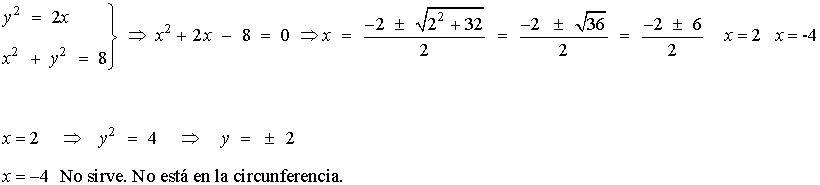
Por tanto los puntos de intersección son ( 2, -2 ) y ( 2, 2 )
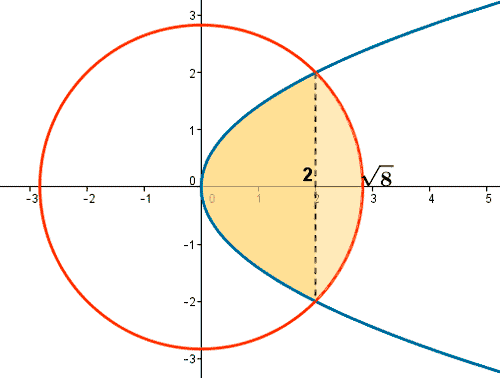
A la vista de la gráfica, el área de la zona sombreada se obtiene como sigue:
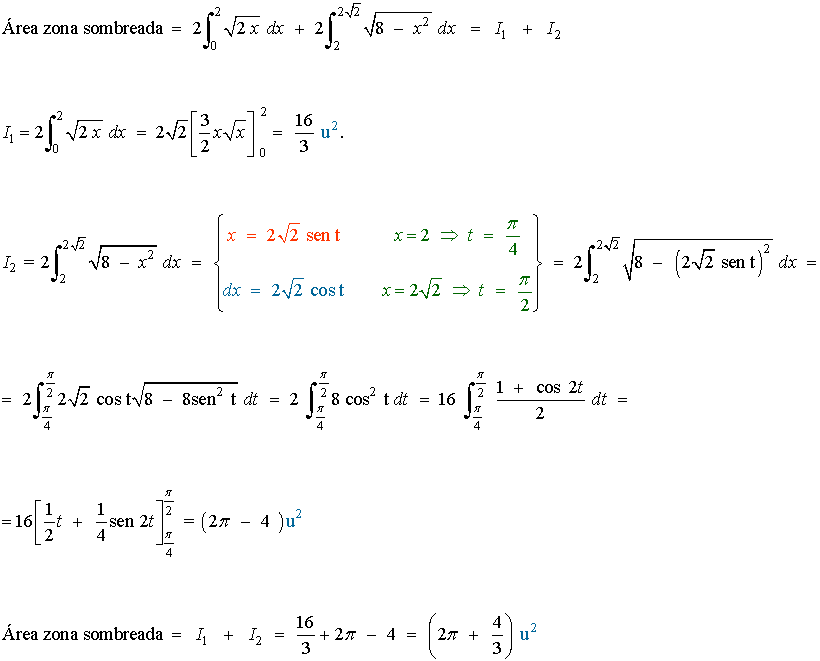
Para obtener el área de la región no sombreada basta con restar al área del círculo el área de la región sombreada:

8) Calcular el área de la figura plana situada en el primer cuadrante y limitada por las curvas x2 + y2 = 4x y y2 = 2x
Empezamos observando que la ecuación x2 + y2 - 4x = 0 es la que nos da la circunferencia de centro en el punto ( 2 , 0 ) y radio 2.
La parábola y2 = 2x es una parábola de eje horizontal y vértice ( 0, 0 ).
Intersección de ambas curvas
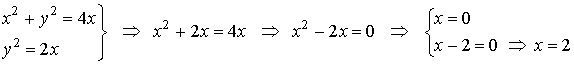
De manera que, el primer cuadrante, las curvas se cortan en los puntos ( 0 , 0 ), y ( 2 , 2 ).
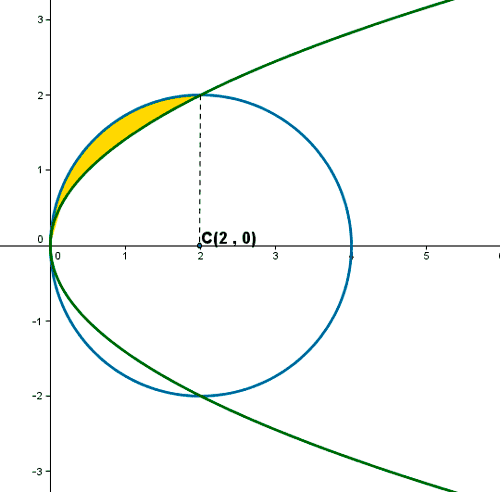
Observamos, que el área que queremos calcular es la del cuarto superior izquierdo de la circunferencia menos el área de la parábola.
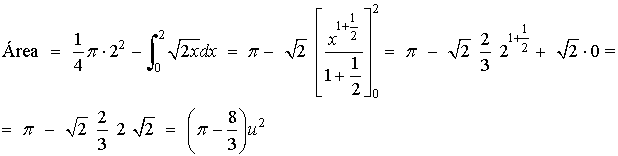
9) Siendo Ln x el logaritmo neperiano de x, halla el área de la superficie sombreada

Observamos que el área pedida es la del rectángulo que tiene como vértices los puntos ( 0, 0 ), ( 0, Ln 3 ), ( 3, 0 ), ( 3, Ln 3 ) menos el área que hay bajo la función f(x) y el eje de abscisas entre las abscisas 1 y 3. Teniendo esto en cuenta:
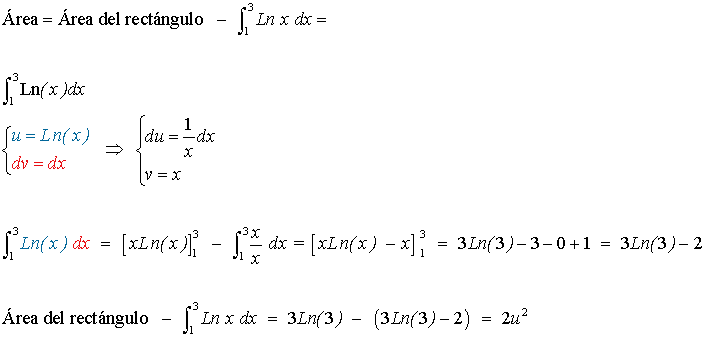
10) Calcula el área comprendida entre la curva:
el eje OX y las rectas verticales que pasan por los puntos de inflexión de dicha curva.
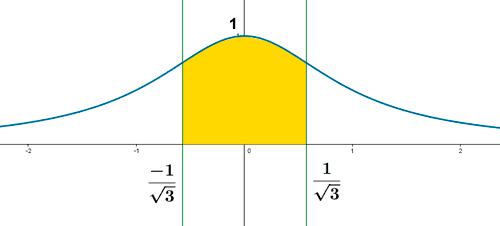
Empezamos calculando los puntos de inflexión. Dichos puntos serán aquellos que verifiquen que la segunda derivada en los mismos es nula.
Observamos ahora que la función es par:

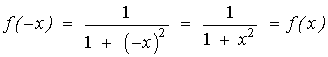
De manera que el área que nos piden puede calcularse como:
El 2 por la simetria par.
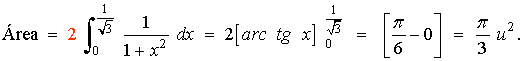
11) Calcula el área del recinto acotado que está limitado por la recta y = 2x y por las curvas:

Intersecciones de la recta con las curvas
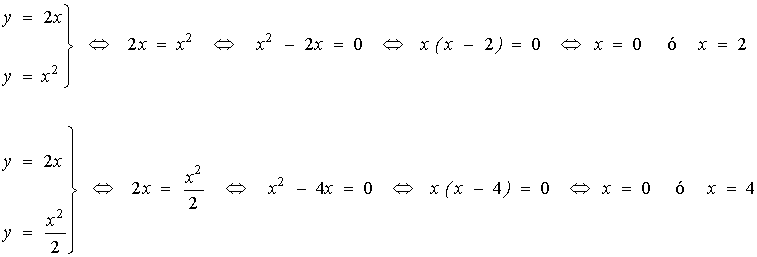
de manera que los puntos de corte son
( 0, 0 ) y ( 2, 4 ) con la primera curva.
( 0, 0 ) y ( 4, 8 ) con la segunda curva.
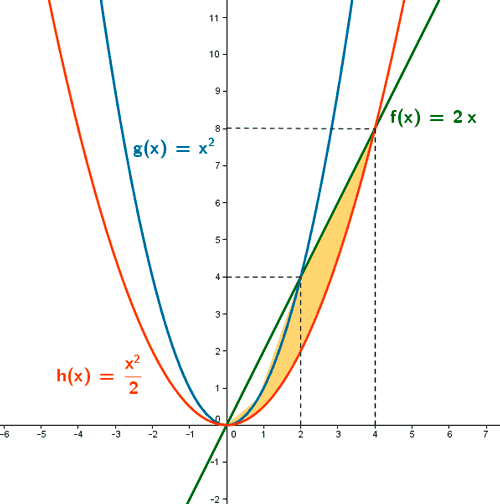
A la vista de la gráfica:


 INICIO
INICIO