Razones trigonométricas de 30o, 45o y 60o
Razones trigonométricas de 45o
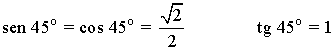
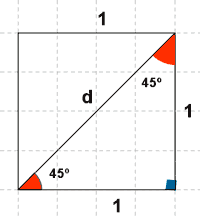
Dibujamos un cuadrado de lado 1 unidad.
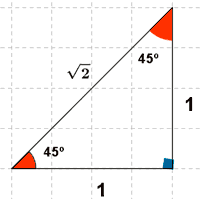
La diagonal del cuadrado divide al cuadrado en dos triángulos rectángulos iguales cuyos ángulos miden 45o.
A continuación, aplicamos el teorema de Pitágoras para hallar el valor de la diagonal:
![]()
Aplicando las definiciones de las razones trigonométricas tenemos que:

De esta forma podemos obtener las razones trigonométricas inversas:
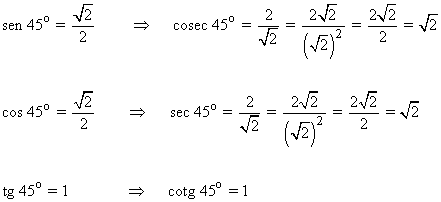
Razones trigonométricas de 30o y 60o
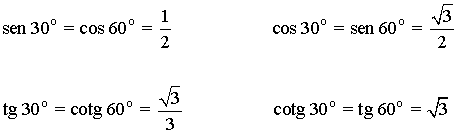
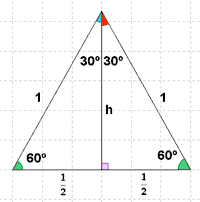
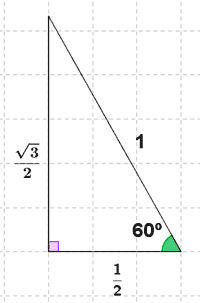
Dibujamos un triángulo equilátero de lado 1 unidad.
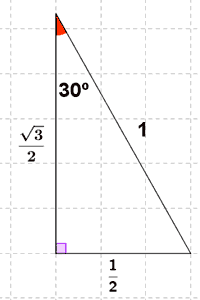
La altura divide en dos triángulos rectángulos iguales cuyos ángulos son de 30o y 60o.
A continuación, aplicamos el teorema de Pitágoras para hallar el valor de la altura:
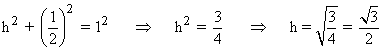
Aplicando las definiciones de las razones trigonométricas tenemos que:

De esta forma podemos obtener las razones trigonométricas inversas:
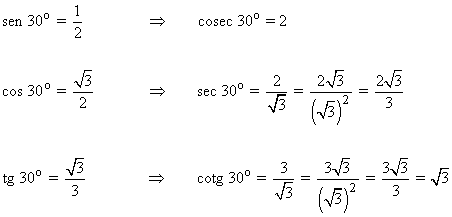
Del triángulo anterior podemos deducir directamente las razones trigonométricas del ángulo de 60o.
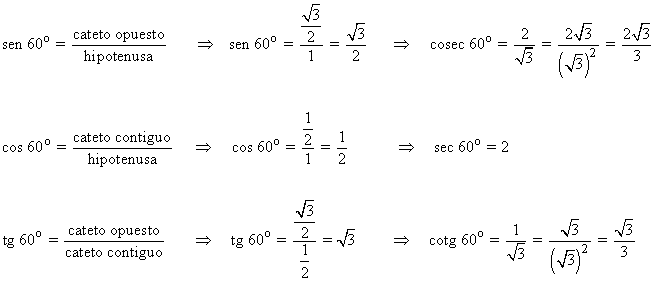
Resumen de las razones trigonométricas de 30o, 45o y 60o
| π/6 30º |
π/4 45º |
π/3 60º |
|
|---|---|---|---|
| seno | |||
| coseno | |||
| tangente | 1 |
Regla nemotécnica para calcular los ángulos notables
| Grados | 0º | 30º | 45º | 60º | 90º |
|---|---|---|---|---|---|
| Radianes | 0 | ||||
| sen | 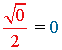 |
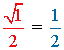 |
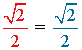 |
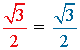 |
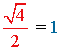 |
| cos | 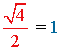 |
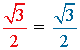 |
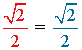 |
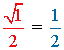 |
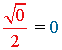 |
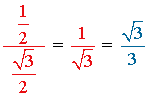 |
 |
 |


 INICIO
INICIO

