Ejercicios resueltos de razones trigonométricas de un ángulo agudo
1) Halla las razones trigonométricas de los ángulos de los siguientes triángulos rectángulos:
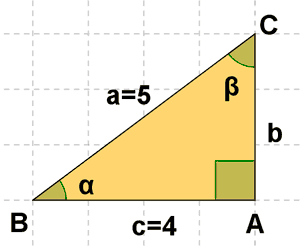
2) Halla las razones trigonométricas de los ángulos de los siguientes triángulos rectángulos:
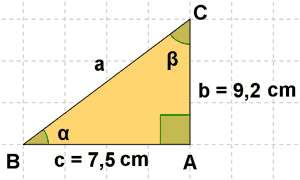
3) Halla las razones trigonométricas de los ángulos de los siguientes triángulos rectángulos:
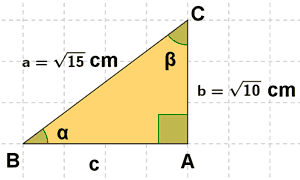
4) Halla las razones trigonométricas de los ángulos de los siguientes triángulos rectángulos:
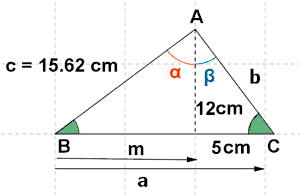
5) Calcular las razones trigonometricas de un ángulo α situado en el primer cuadrante sabiendo que:
![]()
6) Calcular las razones trigonometricas de un ángulo α situado en el segundo cuadrante sabiendo que:
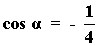
7) Calcular las razones trigonometricas de un ángulo α situado en el tercer cuadrante sabiendo que:
![]()
8) Calcular las razones trigonometricas de un ángulo α situado en el cuarto cuadrante sabiendo que:
![]()
9) Encontrar el ángulo α y las demas razones trigonométricas, sabiendo que:
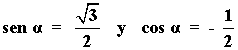
10) Halla las razones trigonométricas del ángulo α en:
sen α = 5/6
11) Determina los valores del seno y coseno si:
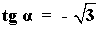
12) Hallar las restantes soluciones trigonometricdas si:
![]()
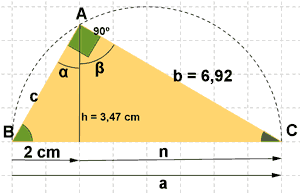
13) Halla las razones trigonométricas de los ángulos del siguiente triángulo rectángulo:
14) Calcular las razones trigonometricas de un ángulo α sabiendo que:
![]()
15) Calcular las razones trigonometricas de un ángulo α sabiendo que:
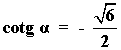
1) Halla las razones trigonométricas de los ángulos de los siguientes triángulos rectángulos:

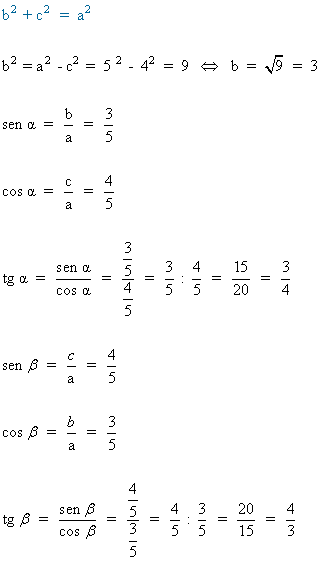
2) Halla las razones trigonométricas de los ángulos de los siguientes triángulos rectángulos:

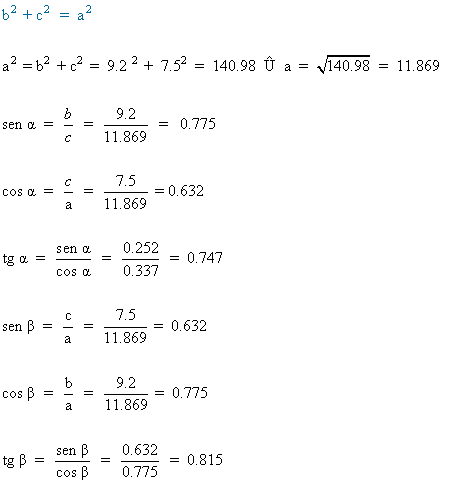
3) Halla las razones trigonométricas de los ángulos de los siguientes triángulos rectángulos:

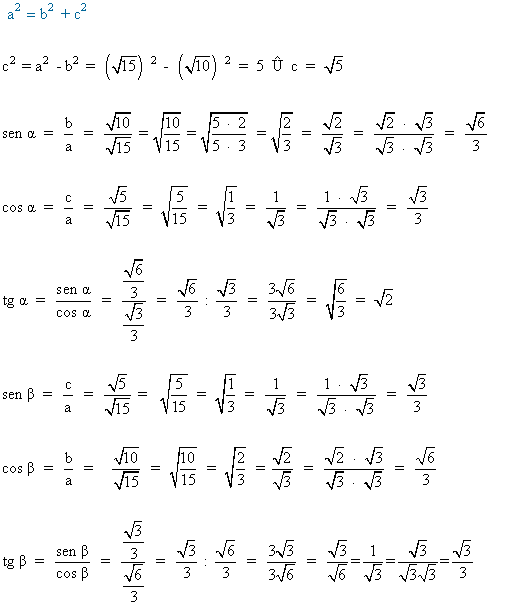
4) Halla las razones trigonométricas de los ángulos de los siguientes triángulos rectángulos:

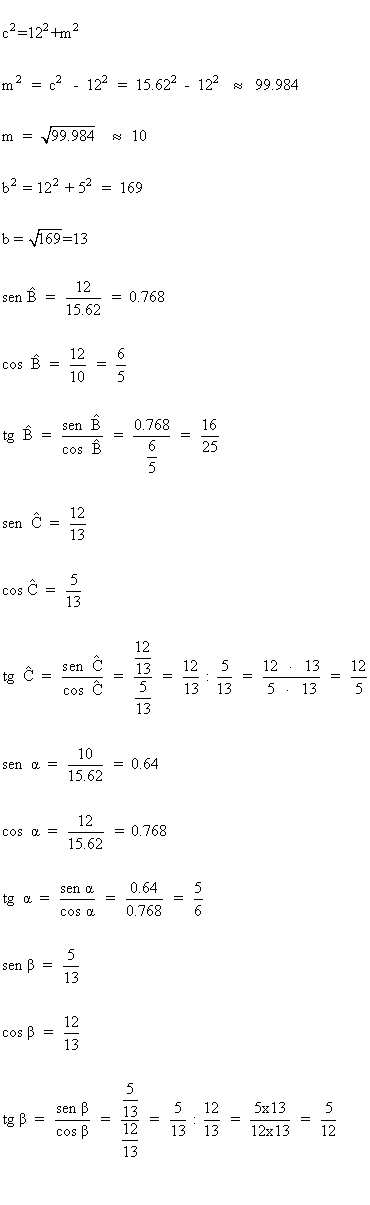
5) Calcular las razones trigonometricas de un ángulo α situado en el primer cuadrante sabiendo que:
![]()
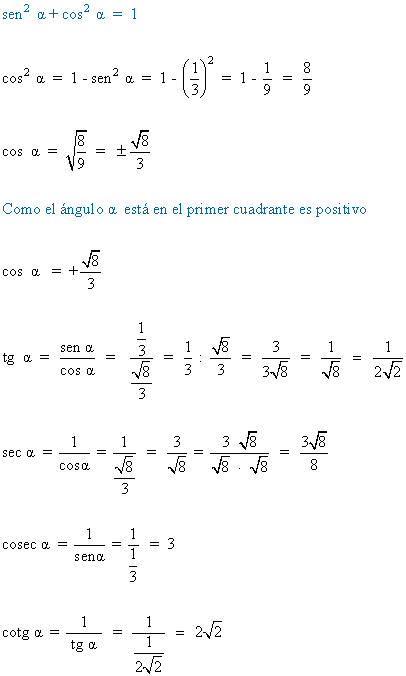
6) Calcular las razones trigonometricas de un ángulo α situado en el segundo cuadrante sabiendo que:
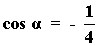
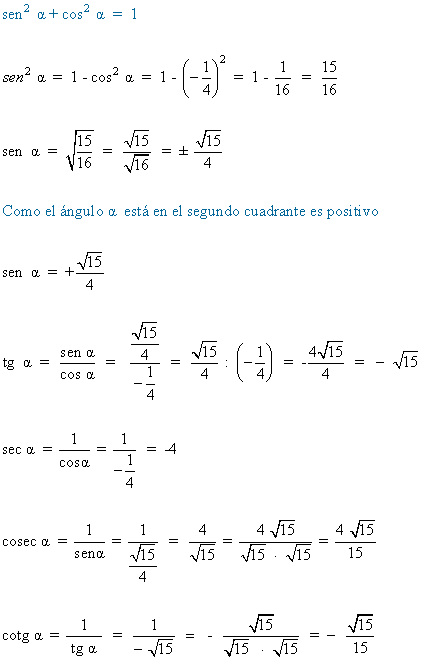
7) Calcular las razones trigonometricas de un ángulo α situado en el tercer cuadrante sabiendo que:
![]()
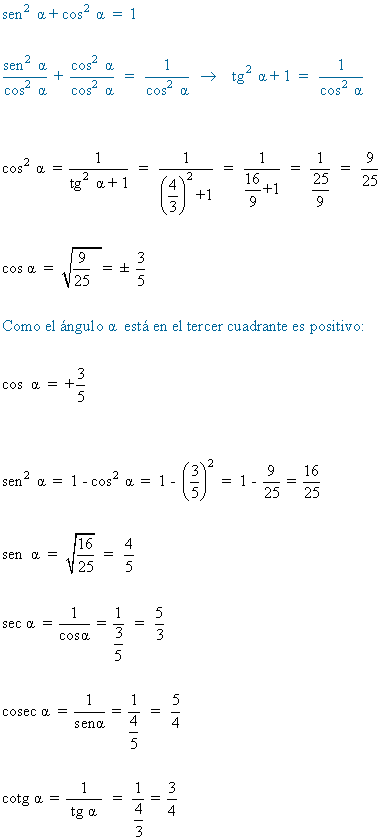
8) Calcular las razones trigonometricas de un ángulo α situado en el cuarto cuadrante sabiendo que:
![]()
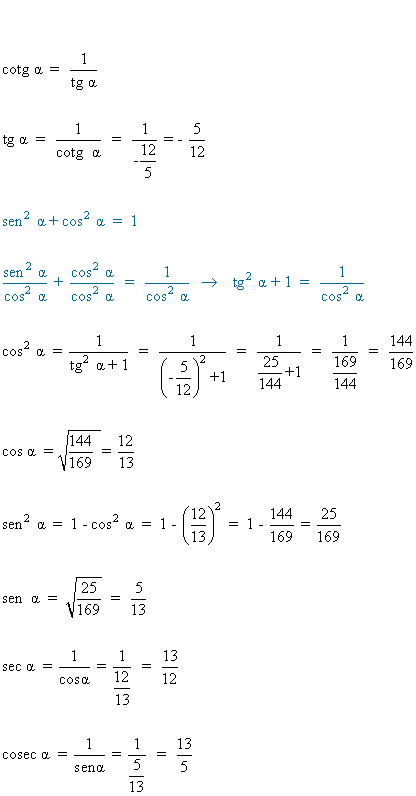
9) Encontrar el ángulo α y las demas razones trigonométricas, sabiendo que:
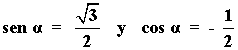
Por ser sen α>0 y cos α <0 , α está en el segundo cuadrante.
a) Por tanto (ver tabla): α=120º
b)
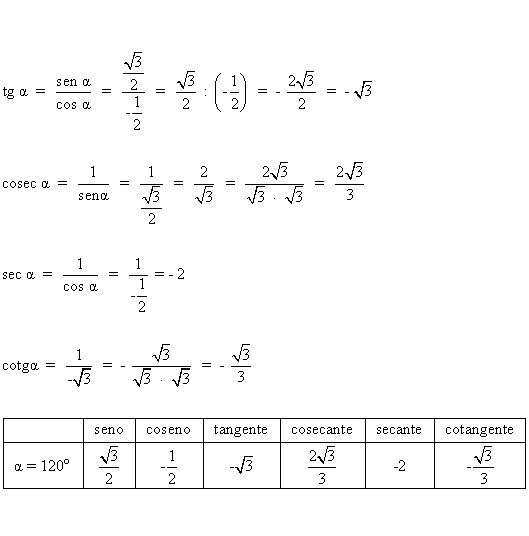
Obtenemos 120º puesto que seno > 0 y coseno > 0 corresponden a un ángulo de 60º. Como el coseno es negativo entonces corresponde al segundo cuadrante, luego α = 180º - 60º = 120º ;
10) Halla las razones trigonométricas del ángulo α en:
sen α = 5/6
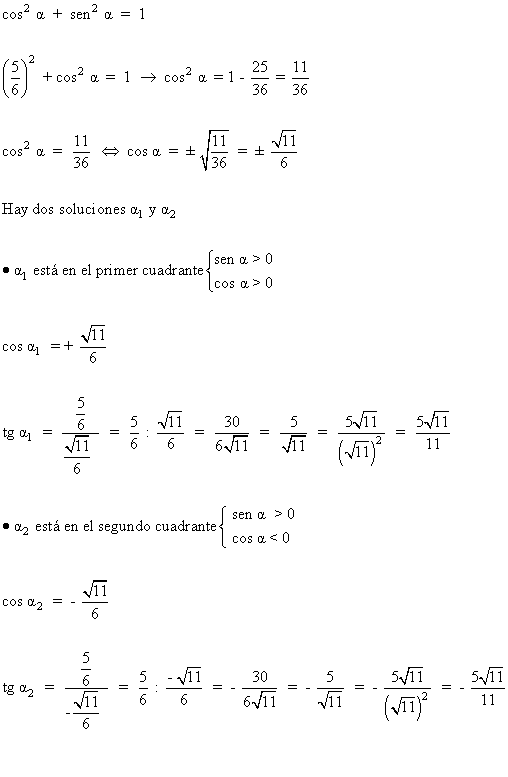
11) Determina los valores del seno y coseno si:
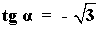
![]()
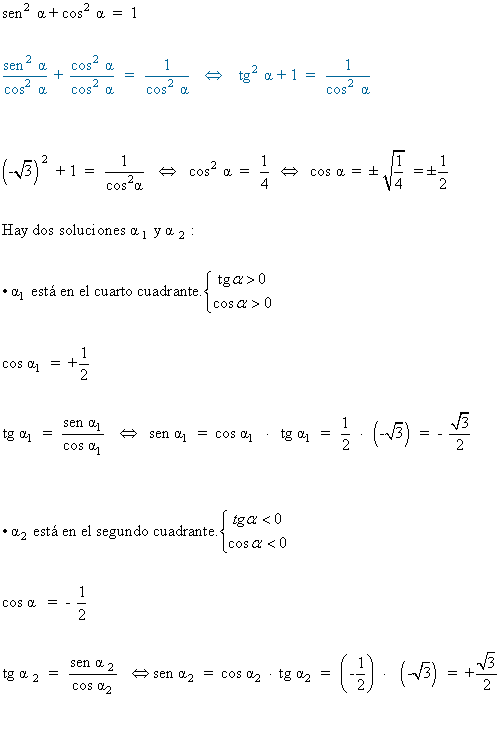
12) Hallar las restantes soluciones trigonometricdas si:
![]()
![]()
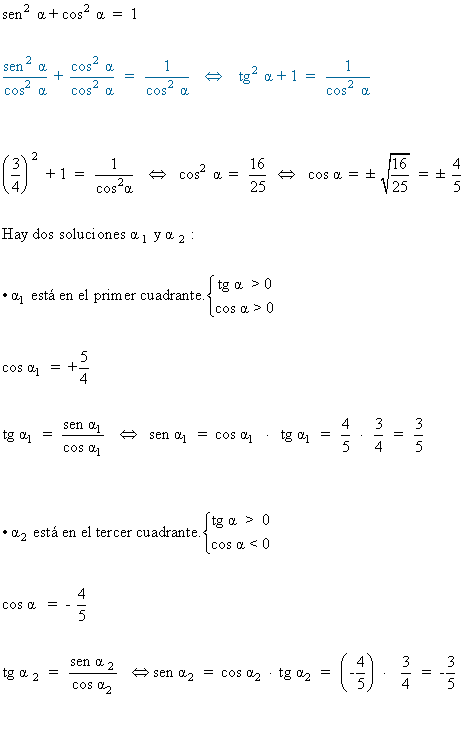
13) Halla las razones trigonométricas de los ángulos del siguiente triángulo rectángulo:

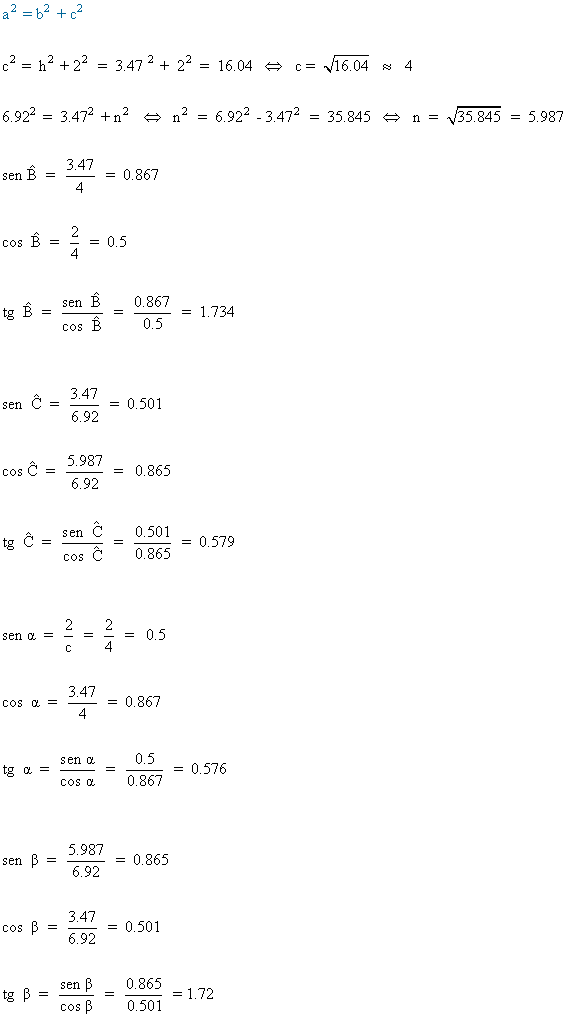
14) Calcular las razones trigonometricas de un ángulo α sabiendo que:
![]()
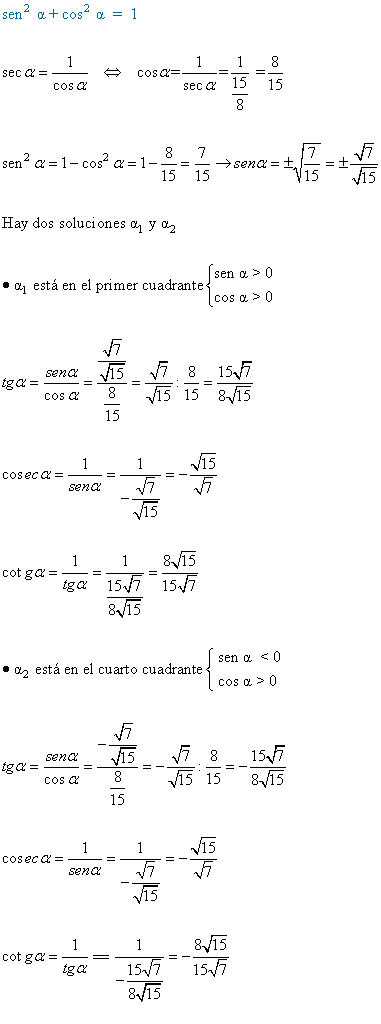
15) Calcular las razones trigonometricas de un ángulo α sabiendo que:
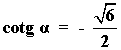
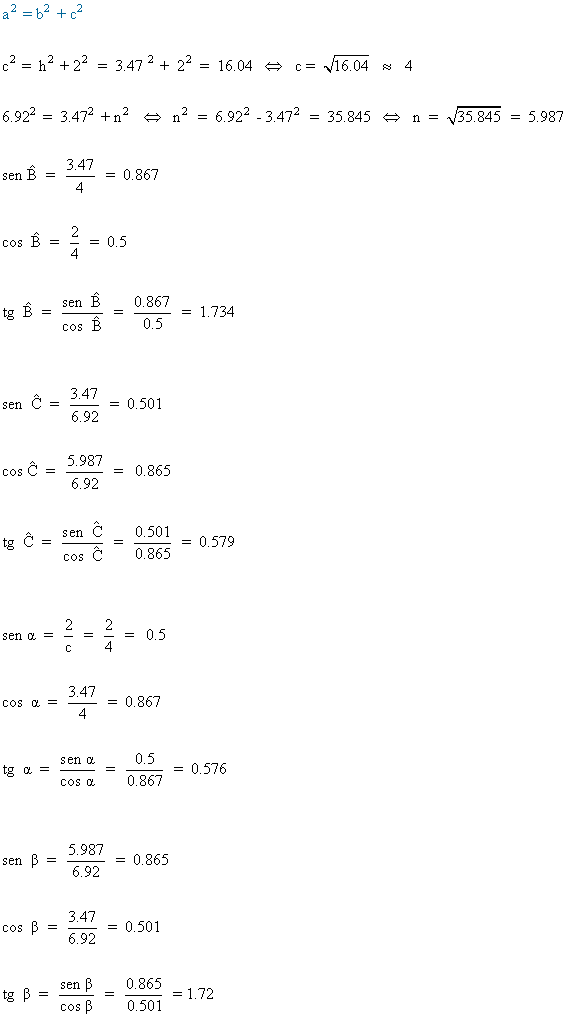


 INICIO
INICIO