Área de un triángulo
Primer método:
Para hallar el área de un triángulo, conocidos sus tres vértices, se aplica la fórmula:
![]()
Para hallar la longitud de la base, calculamos por ejemplo la distancia entre los puntos A y B. Por otro lado, para calcular la altura relativa al lado AB, se halla la ecuación de la recta que pasa por A y B y se calcula la distancia del vertice C a dicha recta.
Ejemplo:
Calcula el área del triángulo delimitado por los vértices A(2, 2) , B(1, 5) y C(-2, 0).
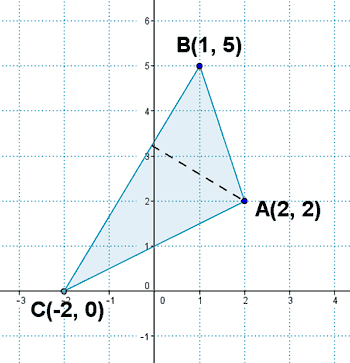
En primer lugar tenemos que calcular la distancia entre los puntos B y C para conocer la base:
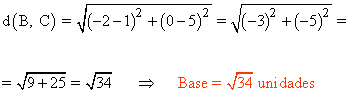
Para calcular la altura del triángulo tenemos que hallar la ecuación de la recta que pasa por los puntos B y C . Calculamos en primer lugar un vector director de dicha recta, por ejemplo, el vector CB:
![]()
Para hallar la recta que pasa por los vértices B y C usamos la ecuación general con el vector director CB y el punto C :
![]()
En último lugar calculamos la distancia del vértice A a la recta que pasa por B y C:
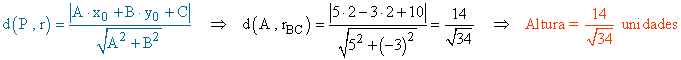
Ahora podemos calcular el área del triángulo:
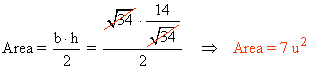
Segundo método o método de Heron:
Siendo los siguientes vértices de un triángulo cualquiera, podemos calcular el área de la siguiente forma:
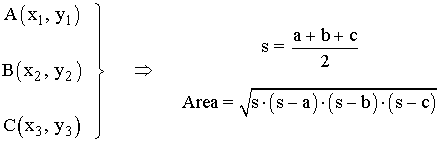
Ejemplo:
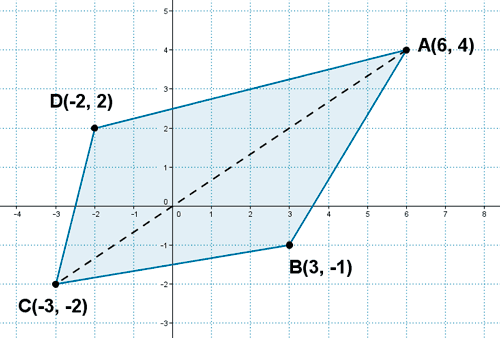
Calcula el área del cuadrilátero de vértices A(6, 4) , B(3, -1) , C(-3, -2) y D(-2, 2) .
Para calcular el área del cuadrilátero vamos a utilizar la fórmula de Herón:
![]()
Por lo tanto tenemos que calcular cuanto miden cada uno de los segmentos, así como la diagonal del cuadrilátero, es decir, la distancia entre los vértices A y C .
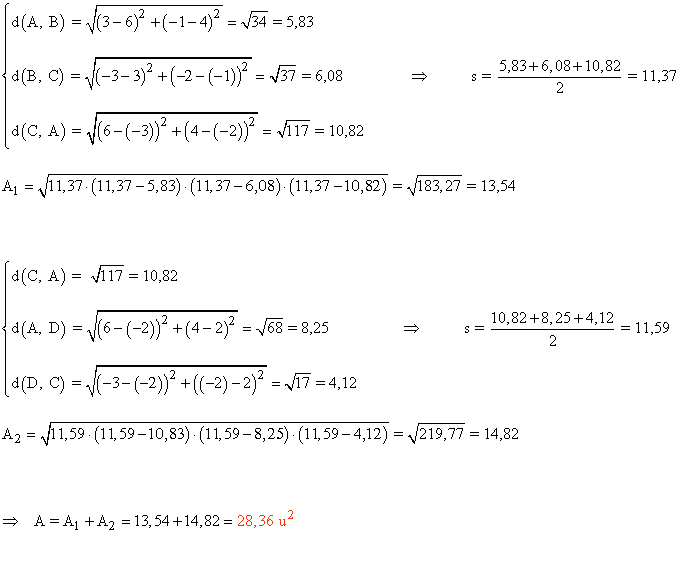
Tercer método:
Siendo los siguientes vértices de un triángulo cualquiera, podemos calcular el área de la siguiente forma:
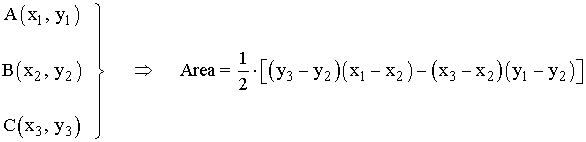
Ejemplo:
Calcula el área del triángulo delimitado por los vértices A(2, 2) , B(1, 5) y C(-2, 0).
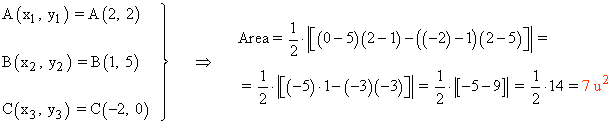
Cuarto método:
Siendo los siguientes vértices de un triángulo cualquiera, podemos calcular el área de la siguiente forma:
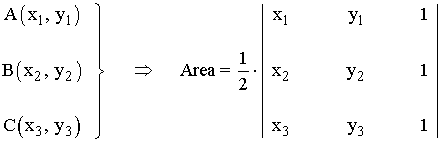
Para calcular el determinante utilizamos la regla de Sarrus. Esquemáticamente podemos representarla como sigue:
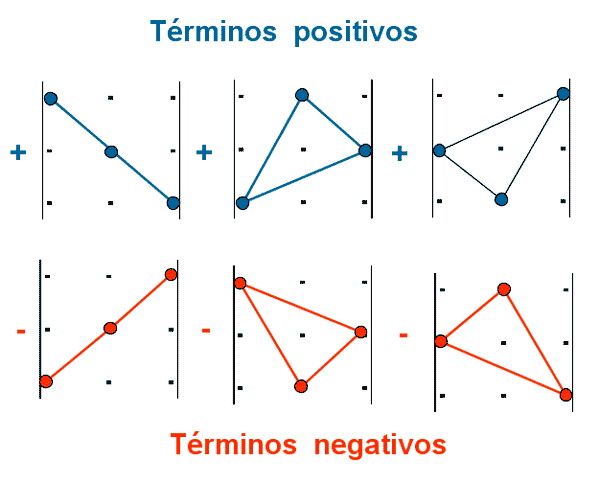
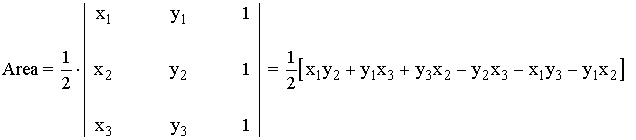
Ejemplo:
Calcula el área del triángulo delimitado por los vértices A(2, 2) , B(1, 5) y C(-2, 0).
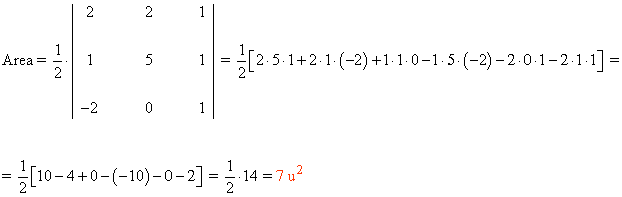


 INICIO
INICIO
