Ejercicios resueltos de mediatrices y distancias
1 ) Halla la ecuación de la mediatriz del segmento de extremos A(3, 4) y B(1, 2) .
2 ) Calcula la distancia del punto P(1, -1) a cada una de las siguientes rectas:
a) x + 3y + 2 = 0
b) y = 2x - 1
c) (x + 1)/2 = (y - 2)/3
d) {x = 1 + t; y = 2 - 4t}
e) 4x + 3y = 2
f) x/2 + y/3 = 1
3 - a ) Calcula la distancia entre las rectas siguientes rectas paralelas:
r: x - 2y - 3 = 0
s: x - 2y + 1 = 40
3 - b ) Calcula la distancia entre las rectas siguientes rectas paralelas:
r: 3x + 4y - 15 = 0
s: 3x + 4y = 40
4 ) Calcula las longitudes de las tres alturas del triángulo determinado por los puntos A(1, 1) , B(1, 3) y C(3, 2) .
5 ) Dados los puntos A(1, -4) y B(-2, 3) y la recta r: x - 2y - 1 = 0 , hallar un punto P que equidiste de A y sea incidente con r .
6 - a ) Halla la ecuación del lugar geométrico de los puntos del plano que distan del eje de abscisas el doble que del eje de ordenadas.
6 - b ) Halla un punto P equidistante de A(3, 1) y B(3, 5) , y que dista el triple del eje de abscisa que del eje de ordenadas.
7 ) Dada la ecuación x - y + 2 = 0 hallar la ecuación de una paralela a dicha recta a una distancia de dos unidades.
8 ) Hallar las coordenadas de un punto de la recta x - y - 1 = 0 que diste 1 unidad de la recta 3x - 4y + 2 = 0 .
9 ) Hallar las coordenadas de un punto P equidistante de 3 puntos dados A(4, 4) , B(5, 3) y C(-1, 3) .
10 - a ) Hallar las ecuaciones de las rectas que son incidentes con el punto A(2, 3) y distan 2 unidades del origen de coordenadas.
10 - b ) De todas las rectas que pasan por el punto A (1 , 2), calcular la pendiente de aquellas cuya distancia al origen es de 1 unidad.
11 ) Determina la recta que dista 3 unidades del punto P (1 , 2) y es perpendicular a r : 3x - 4y + 10 = 0
12 ) Encuentra un punto en la recta -x + 2y -2 = 0 que equidiste de los ejes de coordenadas.
13 ) Halla el punto de la recta 3x - 4y + 2 = 0 que diste de A(-4 , 0) y de B(0 , -4).
14 ) De todas las rectas que pasan por el punto A( 4 , 3 ) calcula recta que determina ssegmentos iguales al cortar a los dos ejes cartesianos.
15 ) Encontrar un punto en el eje de abcisas que este a la misma distancia del punto A(5 , 4) que de la recta:
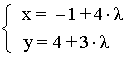
1 ) Halla la ecuación de la mediatriz del segmento de extremos A(3, 4) y B(1, 2) .
Calculamos el punto medio del segmento AB:
![]()
A continuación la pendiente de la mediatriz del segmento AB:
![]()
Aplicamos la ecuación punto pendiente con los datos anteriores:
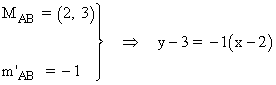
Por lo tanto, la mediatriz del segmento AB es:
![]()
2 ) Calcula la distancia del punto P(1, -1) a cada una de las siguientes rectas:
a) x + 3y + 2 = 0
b) y = 2x - 1
c) (x + 1)/2 = (y - 2)/3
d) {x = 1 + t; y = 2 - 4t}
e) 4x + 3y = 2
f) x/2 + y/3 = 1
La distancia de un punto P(xo, yo) a una recta expresada en su forma general viene dada por la siguiente fórmula:
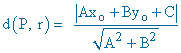
Por lo tanto tenemos que pasar cada una de las rectas dada a su forma general y aplicar la fórmula.
(a)
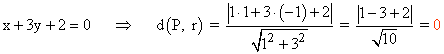
(b)
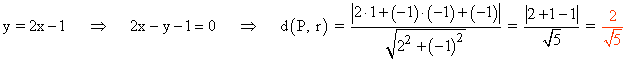
(c)
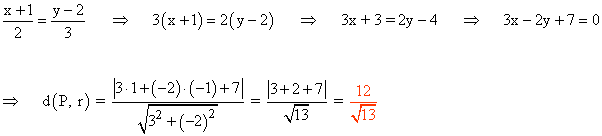
(d)
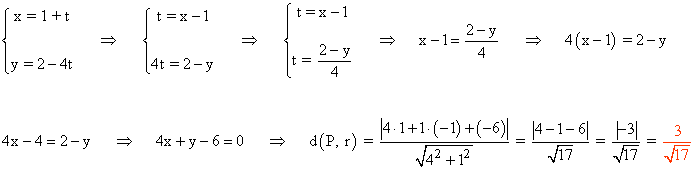
(e)
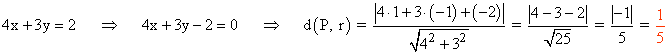
(f)
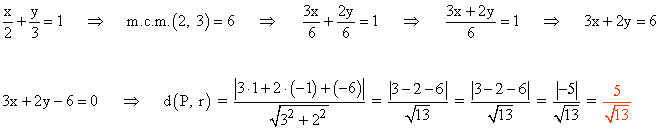
3 - a ) Calcula la distancia entre las rectas siguientes rectas paralelas:
r: x - 2y - 3 = 0
s: x - 2y + 1 = 40
Podemos hacer el cálculo tomando un punto de la recta r y aplicando la fórmula de la distancia entre un punto y una recta:
![]()
O directamente aplicando la fórmula de la distancia entre dos rectas:
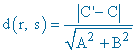
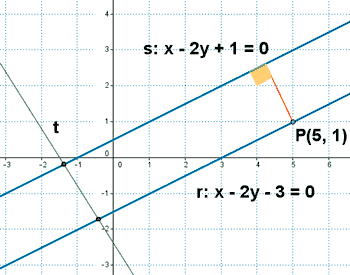
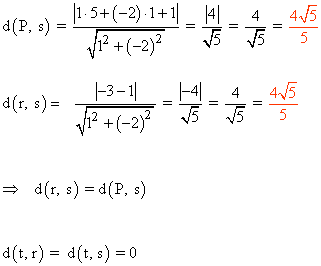
3 - b ) Calcula la distancia entre las rectas siguientes rectas paralelas:
r: 3x + 4y - 15 = 0
s: 3x + 4y = 40
La distancia entre dos rectas r y s expresadas en su forma general viene dada por la siguiente fórmula:
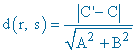
Por lo tanto tenemos que expresar ambas rectas a su forma general y aplicar la fórmula.
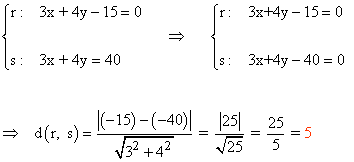
4 ) Calcula las longitudes de las tres alturas del triángulo determinado por los puntos A(1, 1) , B(1, 3) y C(3, 2) .
• Para hallar la longitud de la altura del vértice A tenemos que hallar la recta que pasa por los puntos B y C y a continuación la distancia del punto A a dicha recta:
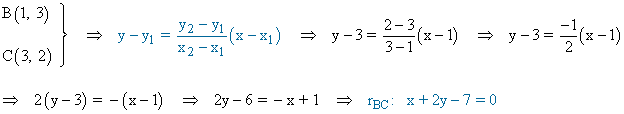
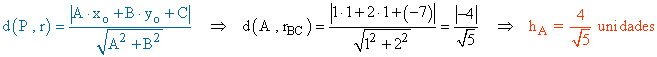
• Para hallar la longitud de la altura del vértice B tenemos que hallar la recta que pasa por los vértices A y C y a continuación la distancia del punto B a dicha recta:
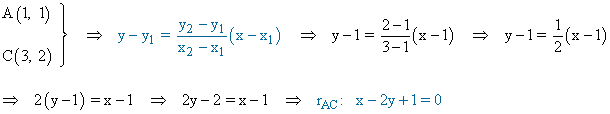
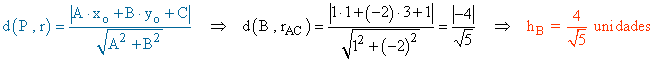
• Para hallar la longitud de la altura del vértice C tenemos que hallar la recta que pasa por los vértices A y B y a continuación la distancia del punto C a dicha recta:
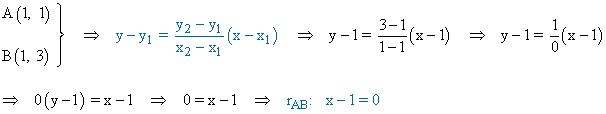
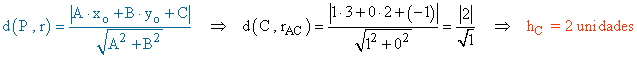
5 ) Dados los puntos A(1, -4) y B(-2, 3) y la recta r: x - 2y - 1 = 0 , hallar un punto P que equidiste de A y sea incidente con r .
Si P(x, y) es el punto que buscamos, se tiene que cumplir:
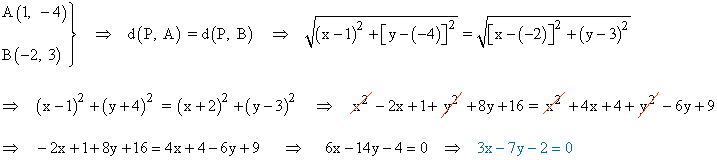
La ecuación de dicha recta es la mediatriz de los puntos A y B . Además, tiene que incidir sobre la recta r , por lo que tenemos que calcular el punto de corte de ambas rectas:
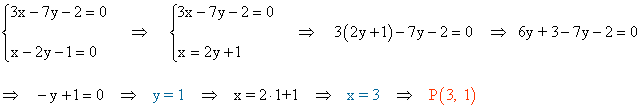
6 - a ) Halla la ecuación del lugar geométrico de los puntos del plano que distan del eje de abscisas el doble que del eje de ordenadas.
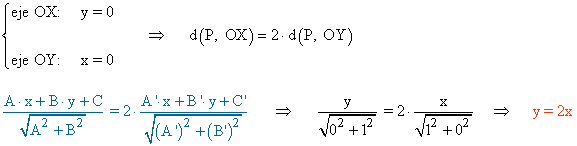
6 - b ) Halla un punto P equidistante de A(3, 1) y B(3, 5) , y que dista el triple del eje de abscisa que del eje de ordenadas.
Si P(x, y) es el punto que buscamos, se tiene que cumplir:
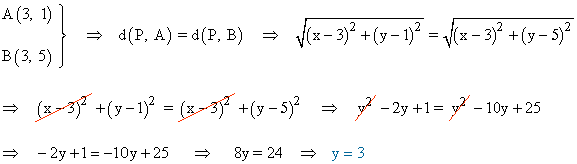
Por otro lado, para que diste el triple del eje de abscisa del eje de ordenadas debe cumplirse lo siguiente:
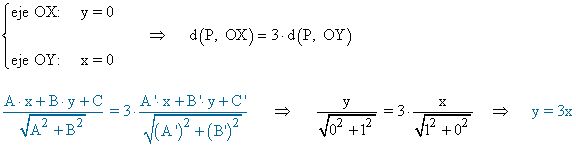
Por último calculamos la intersección entre las dos rectas resultantes:
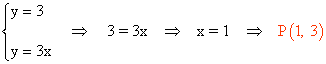
7 ) Dada la ecuación x - y + 2 = 0 hallar la ecuación de una paralela a dicha recta a una distancia de dos unidades.
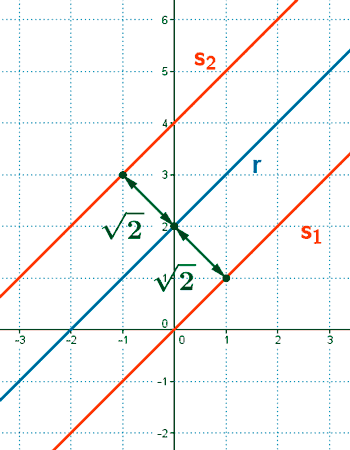
La distancia entre dos rectas r y s expresadas en su forma general viene dada por la siguiente fórmula:
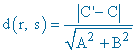
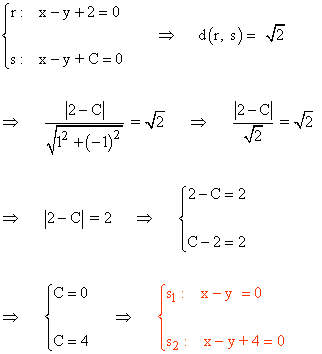
8 ) Hallar las coordenadas de un punto de la recta x - y - 1 = 0 que diste 1 unidad de la recta 3x - 4y + 2 = 0 .
La distancia de un punto a una recta viene dada por la siguiente fórmula:
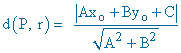
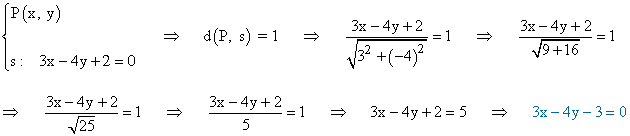
A continuación calculamos el punto de corte de la recta que hemos calculado con la recta x - y - 1 = 0 :
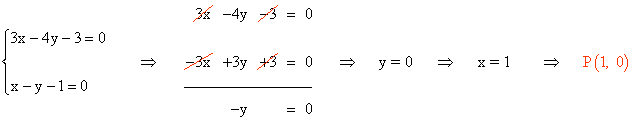
9 ) Hallar las coordenadas de un punto P equidistante de 3 puntos dados A(4, 4) , B(5, 3) y C(-1, 3) .
Si P(x, y) es el punto que buscamos, se tiene que cumplir diste lo mismo de los puntos A y B::
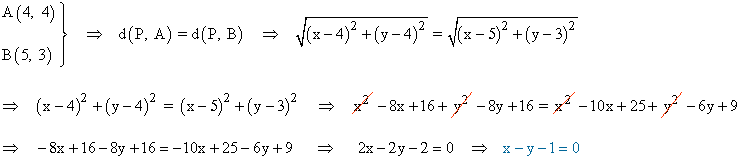
También tiene que cumplirse lo mismo con los puntos B y C:
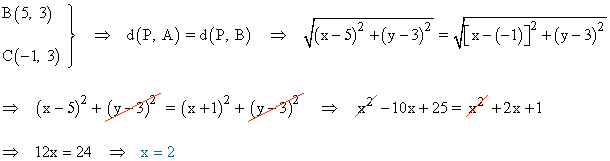
Para calcular el punto P hallamos la intersección de las dos rectas resultantes:
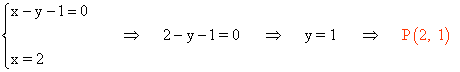
10 - a ) Hallar las ecuaciones de las rectas que son incidentes con el punto A(2, 3) y distan 2 unidades del origen de coordenadas.
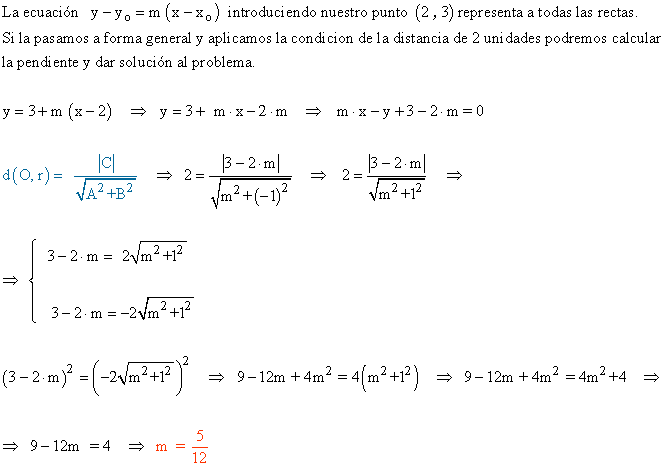
10 - a ) De todas las rectas que pasan por el punto A ( 1 , 2 ), calcular la pendiente de aquellas cuya distancia al origen es de 1 unidad.
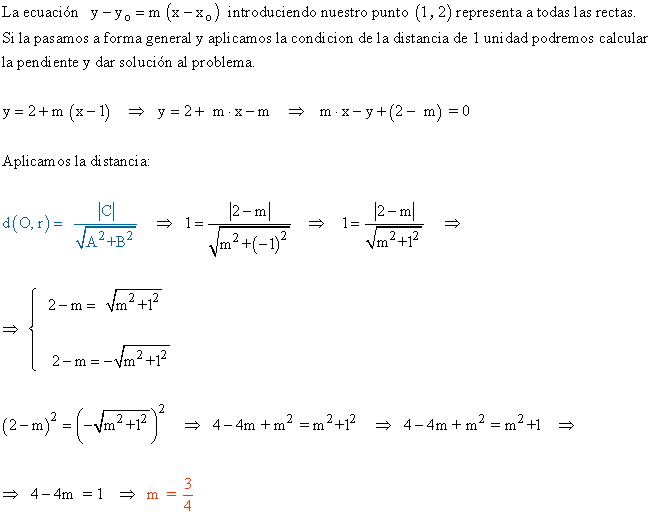
11 ) Determina la recta que dista 3 unidades del punto P ( 1 , 2 ) y es perpendicular a r : 3x - 4y + 10 = 0
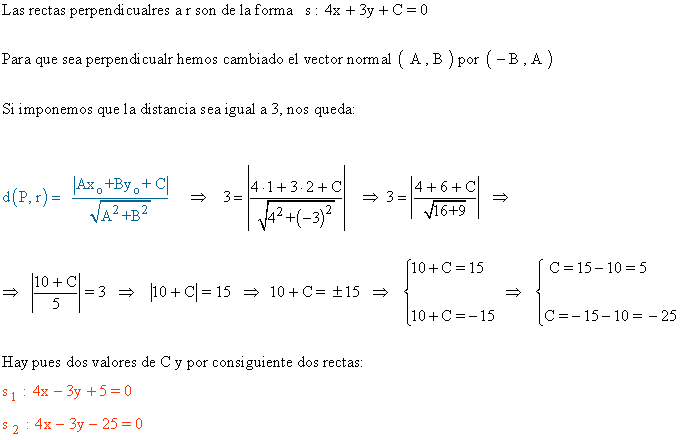
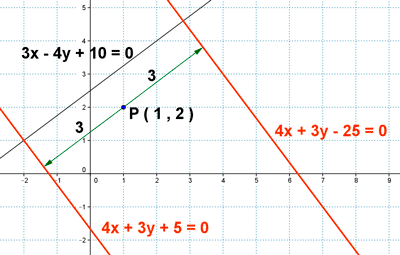
12 ) Encuentra un punto en la recta -x + 2y -2 = 0 que equidiste de los ejes de coordenadas.
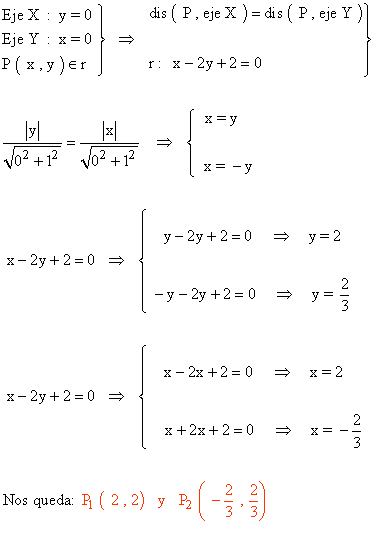
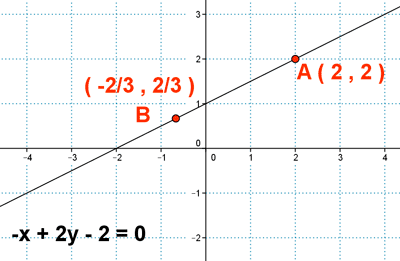
13 ) Halla el punto de la recta 3x - 4y + 2 = 0 que diste de A(-4 , 0) y de B(0 , -4).
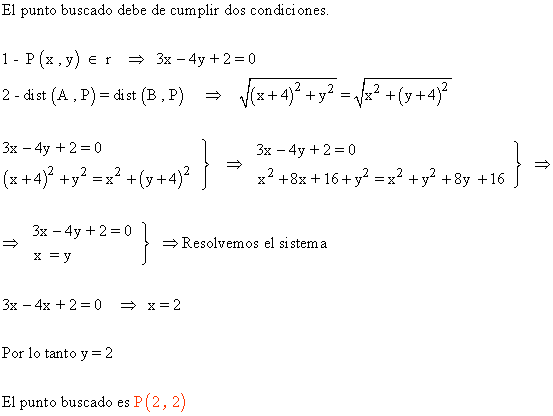
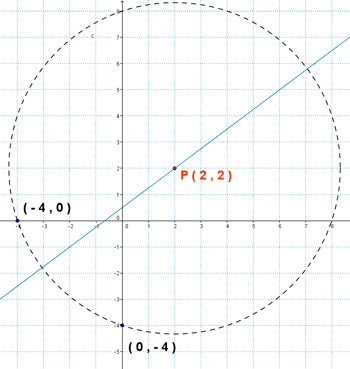
14 ) De todas las rectas que pasan por el punto A(4 , 3) calcula recta que determina ssegmentos iguales al cortar a los dos ejes cartesianos.
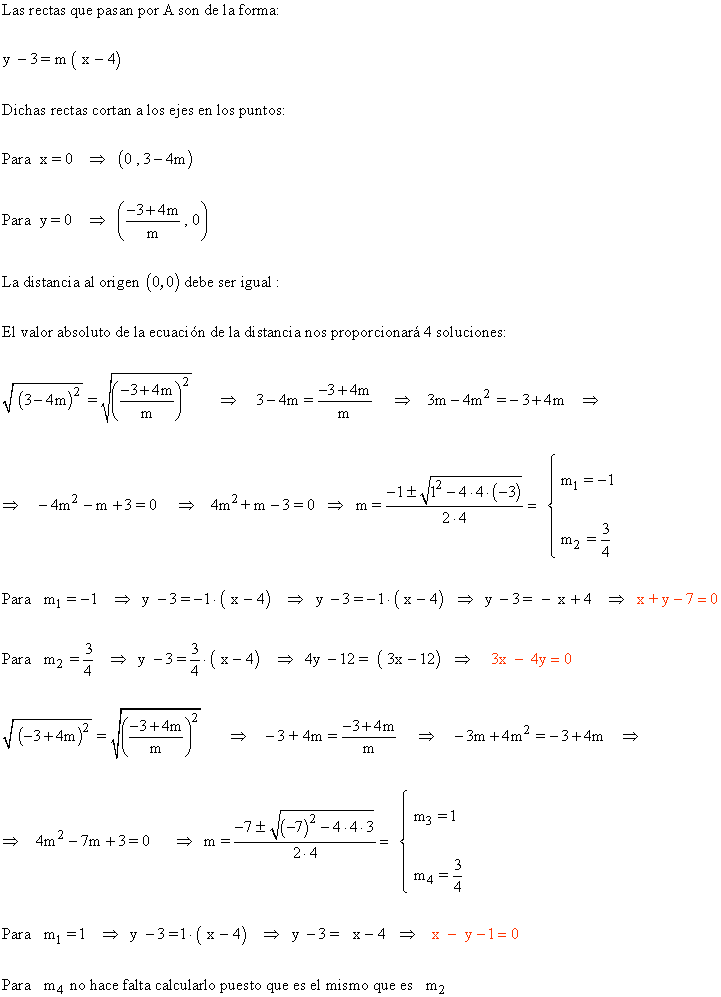
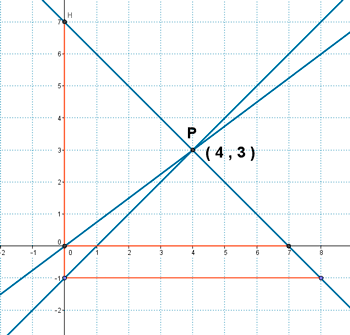
15 ) Encontrar un punto en el eje de abcisas que este a la misma distancia del punto A(5 , 4) que de la recta:
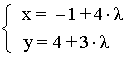
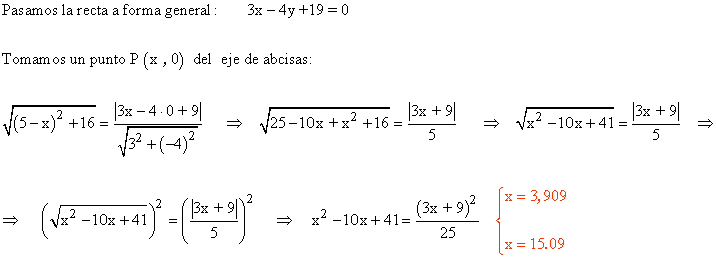


 INICIO
INICIO