Función de proporcionalidad inversa.
Una función de proporcionalidad inversa es una función que relaciona dos magnitudes inversamente proporcionales.
Su expresión algebraica es del tipo 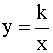 ( k ≠ 0 ), siendo k la constante de proporcionalidad inversa.
( k ≠ 0 ), siendo k la constante de proporcionalidad inversa.
Características de la función de proporcionalidad inversa.
- Dom f ( x ) = R - { 0 }, o lo que es lo mismo : su dominino está formado por los intervalos ( - ∞ , 0 ) y ( 0, ∞ ).
- Rec f ( x ) = R - { 0 }, su recorrido está formado por los intervalos ( - ∞ , 0 ) y ( 0, ∞ ).
- Es impar :
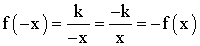
- Su gráfica es una curva con dos ramas llamada hipérbola, que no corta a los ejes.
-
Si la constante de proporcionalidad, k, es un número positivo ( k > 0 ), la función es decreciente en su dominio.
Si k es negativo ( k < 0 ), la función es creciente en su dominio. - Tiene dos asíntotas : los dos ejes de coordenadas.
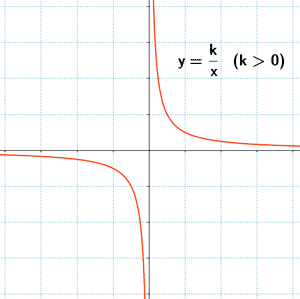
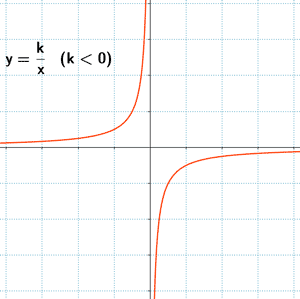
Asíntotas.
Una asíntota es la recta a la que se acerca indefinidamente la gráfica de una función.
Analicemos la funcion ![]() :
:
Si evaluamos la función en puntos próximos a 0 tenemos :
| x | 1 | 0,1 | 0,01 | 0,001 | 0,0001 | 0,00001 |
|---|---|---|---|---|---|---|
| y | 1 | 10 | 100 | 1000 | 10000 | 100000 |
Por lo tanto : Cuando x → 0 +, f ( x) → + ∞,
Diremos que la función tiene una asíntota vertical en x = 0.
Si evaluamos la función en puntos grandes :
| x | 1 | 10 | 100 | 1000 | 10000 | 100000 |
|---|---|---|---|---|---|---|
| y | 1 | 0,1 | 0,01 | 0,001 | 0,0001 | 0,00001 |
En este caso tenemos que cuando x → + ∞ , f ( x ) → 0
La función tiene una asíntota horizontal en y = 0.
Representando los valores obtenidos en las tablas anteriores, obtenemos la gráfica de f ( x ).
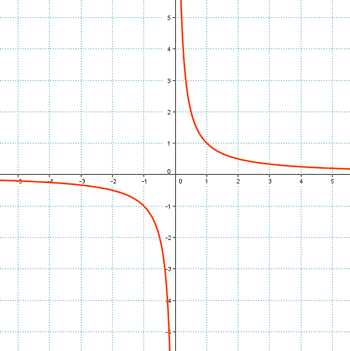
Asíntotas en las funciones de proporcionalidad inversa.
Si k > 0
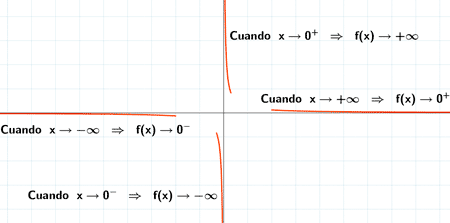
Si k < 0
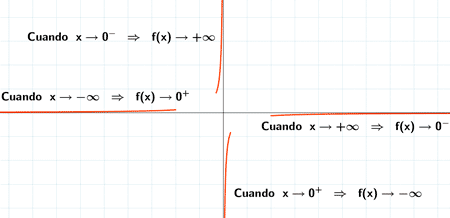
Ejemplo 1 :
Realiza el estudio completo de las siguientes funciones de proporcionalidad inversa.
![]()
1) Puntos de corte con los ejes:
Para x = 0 la función f(x) no está definida puesto que f(0) = 3/0 (no real).
Para x = 0 la función g(x) no está definida puesto que g(0) = - 3/0 (no real).
2) Simetrías:
Las funciones f(x) y g(x) son impares, es decir, son simétricas respecto al eje de coordenadas.
![]()
![]()
3) Crecimiento o decrecimiento:
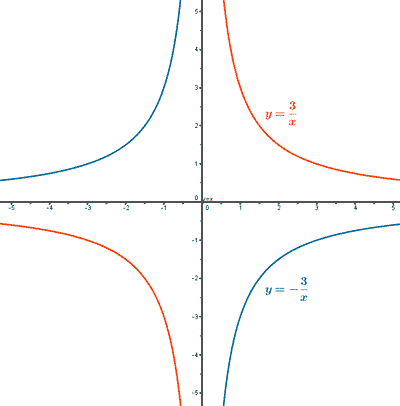
Para la función f(x) tenemos que k > 0 , por lo tanto la función es decreciente y la gráfica está en el primer y tercer cuadrante. Es decir, la función es decreciente en (- ∞, 0) ∪ (0, + ∞).
Para la función g(x) tenemos que k < 0 , por lo tanto la función es creciente y la gráfica está en el segundo y cuarto cuadrante. Es decir, la función es creciente en (- ∞, 0) ∪ (0, + ∞).
4) Tabla de valores:
Construimos una tabla de valores.
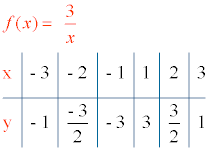
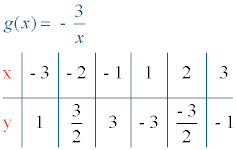


 INICIO
INICIO

