Funciones exponenciales
Las funciones exponenciales son las funciones que tienen la variable independiente x en el exponente, es decir, son de la forma:
![]()
Las características generales de las funciones exponenciales son:
1) El dominio de una función exponencial es R.
2) Su recorrido es (0, +∞) .
3) Son funciones continuas.
4) Como a0 = 1 , la función siempre pasa por el punto (0, 1).
La función corta el eje Y en el punto (0, 1) y no corta el eje X.
5) Como a1 = a , la función siempre pasa por el punto (1, a).
6) Si a > 1 la función es creciente.
Si 0 < a < 1 la función es decreciente.
7) Son siempre cóncavas.
8) El eje X es una asíntota horizontal.
- Si a > 1 :
Al elevar un número mayor que 1 a cantidades negativas cada vez más grandes, el valor de la potencia se acerca a cero, por tanto :
Cuando x → - ∞ , entonces a x → 0 - Si 0 < a < 1 :
Ocurre lo contrario que en el caso anterior :
Cuando x → + ∞ , encontes a x → 0
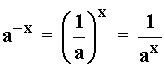
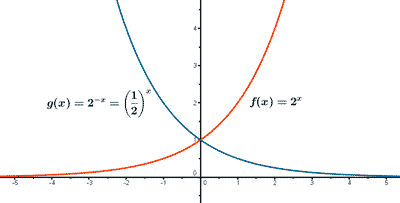
Ejemplo de funciones exponenciales:
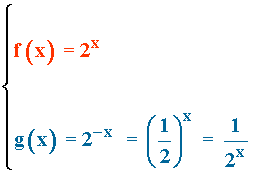
1) Dominio:
El dominio de las funciones exponenciales es R.
Dom(f) = Dom(g) = R .
2) Recorrido:
El recorrido de las funciones exponenciales es (0, + ∞) .
Im(f) = Im(g) = (0, + ∞) .
3) Puntos de corte:
f(0) = 20 = 1 , el punto de corte con el eje Y es (0, 1).
g(0) = - 20 = 1 , el punto de corte con el eje Y es (0, 1).
La funciones f(x) y g(x) no cortan al eje X.
4) Crecimiento y decrecimiento:
La función f(x) es creciente ya que a > 1 .
La función g(x) es decreciente ya que 0 < a < 1 .
5) Concavidad y convexidad:
Las funciones f(x) y g(x) son cóncavas.
6) Asíntotas:
Las funciones f(x) y g(x) tienen una asintota en el eje X.
En f ( x ) a > 1 y en g ( x ) 0 < a < 1.
f ( x ) :
| x | - 5 | - 10 | - 20 |
|---|---|---|---|
| y | 0,03125 | 0,00097 | 9,53 · 10 - 7 |
Cuando x → - ∞ , entonces 2 x → 0
g( x ) :
| x | 5 | 10 | 30 |
|---|---|---|---|
| y | 0,03125 | 0,00097 | 9,53 · 10 - 7 |
Cuando x → ∞ , entonces a - x → 0
7) Tabla de valores:
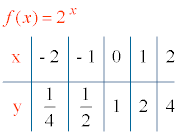
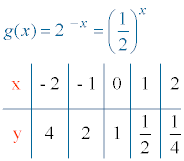
Resumen de las propiedades de la función exponencial ax
| 1 | La función exponencial es la inversa de la logarítmica: y = ax ⇔ x = log y |
|---|---|
| 2 | La función y = ax tiene por dominio R y por recorrido y > 0 |
| 3 | La función y = ax es continua, creciente e inyectiva en todo su dominio. |
| 4 | La función y = ax es cóncava hacia arriba en todo su dominio. |
Funciones de la forma f (x) = k · a x
La gráfica de una función de este tipo tiene la mismas características que la de f (x) = a x. La única diferencia es que el punto de corte con el eje de ordenadas es ( 0, k )
Ejemplo 2 :
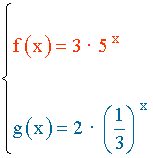
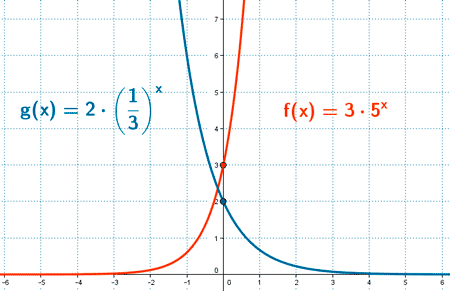
1) Dominio:
El dominio de las funciones exponenciales es R.
Dom(f) = Dom(g) = R .
2) Recorrido:
El recorrido de las funciones exponenciales es (0, + ∞) .
Im(f) = Im(g) = (0, + ∞) .
3) Puntos de corte:
f(0) =3 · 50 = 3 , el punto de corte con el eje Y es (0, 3).
g(0) = 2 · ( 1 / 3 ) 0 = 2 , el punto de corte con el eje Y es (0, 2).
La funciones f(x) y g(x) no cortan al eje X.
4) Crecimiento y decrecimiento:
La función f(x) es creciente ya que a > 1 .
La función g(x) es decreciente ya que 0 < a < 1 .
5) Concavidad y convexidad:
Las funciones f(x) y g(x) son cóncavas.
6) Asíntotas:
Las funciones f(x) y g(x) tienen una asintota en el eje X.
En f ( x ) a > 1 y en g ( x ) 0 < a < 1.
f ( x ) :
Cuando x → - ∞ , entonces 2 x → 0
g( x ) :
Cuando x → ∞ , entonces a - x → 0
7) Tabla de valores:
f (x) :
| x | - 1 | 0 | 1 |
|---|---|---|---|
| y | 0,6 | 3 | 15 |
g (x) :
| x | - 1 | 0 | 1 |
|---|---|---|---|
| y | 6 | 2 | 0,6 |
Funciones de la forma f (x) = a k · x
Las funciones de la forma f (x) = a k · x, con k ≠ 0, son funciones de tipo exponencial con base a k
f (x) = a k · x = ( a k ) x
Ejemplo 3 :
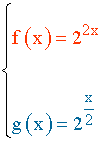
1) Dominio:
El dominio de las funciones exponenciales es R.
Dom(f) = Dom(g) = R .
2) Recorrido:
El recorrido de las funciones exponenciales es (0, + ∞) .
Im(f) = Im(g) = (0, + ∞) .
3) Puntos de corte:
f(0) =2 2 · 0 = 2 0 = 1, el punto de corte con el eje Y es (0, 1).
g(0) = 2 0/2 = 2 0 = 1, el punto de corte con el eje Y es (0, 1).
La funciones f(x) y g(x) no cortan al eje X.
4) Crecimiento y decrecimiento:
La función f(x) es creciente ya que a > 1 .
La función g(x) es creciente ya que a > 1 .
5) Concavidad y convexidad:
Las funciones f(x) y g(x) son cóncavas.
6) Asíntotas:
Las funciones f(x) y g(x) tienen una asintota en el eje X.
En f ( x ) a > 1 y en g ( x ) a > 1.
f ( x ) :
Cuando x → - ∞ , entonces 2 2x → 0
g( x ) :
Cuando x → - ∞ , entonces 2 x/2 → 0
7) Tabla de valores:
f (x) :
| x | - 1 | 0 | 1 |
|---|---|---|---|
| y | 0,25 | 1 | 4 |
g (x) :
| x | - 2 | 0 | 2 |
|---|---|---|---|
| y | 0,50 | 1 | 2 |
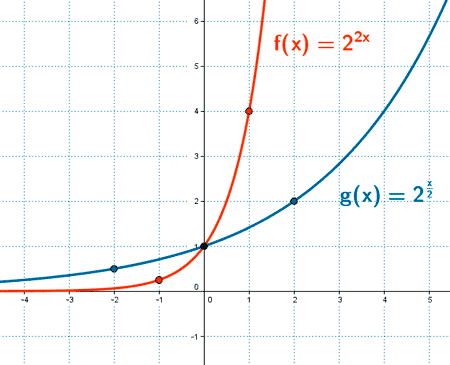


 INICIO
INICIO

