Criterios de divisibilidad.
Divisibilidad por 2.
Tomamos el conjunto de los múltiplos de 2 :
M ( 2 ) = { 2, 4, 6, 8, 10, 12, ... , 100, 102, ... }
La cifra correspondiente a las unidades de estos números son o bien 0 o bien un número par.
Un número es divisible por 2 si termina en 0 o en cifra par.
Divisibilidad por 3.
Tomamos el conjunto de los múltiplos de 3 :
M ( 3 ) = { 3, 6, 9, 12, 15, 18, ... , 120, 123, ... }
La suma de las cifras de estos números es un múltiplo de 3 :
![]()
Un número es divisible por 3 si la suma de sus cifras es un múltiplo de 3.
Divisibilidad por 4.
Tomamos el conjunto de los múltiplos de 4 :
M ( 4 ) = { 4, 8, 12, 16, 20, ... , 100, 104, 108, ... }
Los múltiplos terminan en 00 o la suma de sus dos últimas cifras es múltiplo de 4.
Un número es divisible por 4 si lo es el número formado por sus dos últimas cifras o termina en 00.
Divisibilidad por 5.
Tomamos el conjunto de los múltiplos de 5 :
M ( 5 ) = { 5, 10, 15, 20, 25, 30, ... , 150, 155, 160, ... }
La cifra de las unidades de esos números es o bien 0 o bien 5.
Un número es divisible por 5 si termina en 0 o en 5.
Divisibilidad por 6.
Tomamos el conjunto de los múltiplos de 6 :
M ( 6 ) = { 6, 12, 18, 24, 30, ... , 300, 306, 312, 318, ... }
Un número es divisible por 6 si es divisible a la vez por 2 y por 3.
Divisibilidad por 9.
Tomamos el conjunto de los múltiplos de 9 :
M ( 9 ) = { 9, 18, 27, 36, 45, ... , 180, 189, 198, ... }
La suma de las cifras de esos números es un múltiplo de 9 :
![]()
Un número es divisible por 9 si la suma de sus cifras es múltiplo de 9.
Divisibilidad por 11.
Un número es divisible por 11 si la resta entre la suma de sus cifras de lugar par y la suma de sus cifras de lugar impar ( o viceversa ) es 0 o múltiplo de 11.
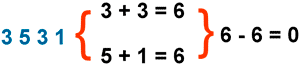


 INICIO
INICIO

