Representación de funciones trigonométricas
Representa gráficamente la función: y = sen2 x
Función trigonométrica.
• Dom(f) = R = (-∞, +∞)
• Im(f) : Calcularemos su imagen o recorrido a través de su función invesa
y = sen2(x) ⇒ ±√y = sen(x) ⇒ arcsen(±√y) = x
Intercambiamos las variables y estudiamos el dominio de la nueva función: y = arcsen(±√x)
• El dominio de la función arc sen(x) es: [-1 , 1]
• La raíz cuadrada está bien definida sólo en los números positivos: [0 , ∞)
Por tanto, su dominio es: [-1 , 1] ∩ [0 ,∞) = [0 , 1]
O lo que es lo mismo, la imagen de nuestra función es: Im(f) = [0 , 1]
Vamos a escribir f(x) de otra forma equivalente que nos permita calcular su período.
Usaremos la fórmula del coseno del ángulo doble: cos(2x) = cos2(x) - sen2(x)
Y también: 1 = cos2(x) + sen2(x)
cos(2x) = cos2(x) - sen2(x) ⇔ cos(2x) = (1 - sen2(x) ) - sen2(x) ⇔ cos(2x) = 1 - 2sen2(x) ⇔
⇔ 2sen2(x) = 1 - cos(2x) ⇔ sen2(x) = (1 - cos(2x) )/2
Ahora sí sabemos calcular su período teniendo en cuenta que el período de la función coseno es 2π :
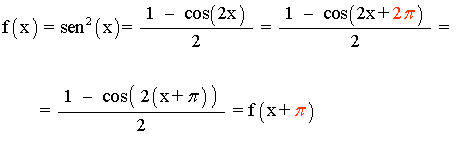
El período de f(x) es T = π .
Por tanto haremos el estudio de la función en el intervalo: [0 , π )
Continuidad y tipos de discontinuidad
La función es continua en toda la recta real R por ser una función trigonométrica.
Calculamos los puntos de corte que hayan dentro del primer período de nuestra función.
Puntos de corte con el eje Y:
Si x = 0 ⇒ y = sen2(0) ⇒ y = 0 ⇒ (0 , 0)
Puntos de corte con el eje X:
Si y = 0 ⇒ 0 = sen2(x) ⇒ 0 = ± sen(x) ⇒ x = 0 ó x = π
Luego los puntos de corte con el eje X son: (0 , 0) , (π , 0)
Como los puntos de corte con el eje OX son x = 0 y x = π , y el período de la función es [0 , π ) , estudiaremos el signo en el intervalo: (0, π)
| Intervalo | (0, π) |
|---|---|
| Punto de prueba | f(π/2) > 0 |
| Signo de f (x) | + |
En la gráfica se marcan los puntos de corte con los ejes y las regiones donde no hay curva.
f(- x) = sen2(-x) = (- sen(x))2 = sen2 x = f(x) ⇒ Tiene simetría par.
sen (-x) = - sen x
Asíntotas
No tiene asíntotas.
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
f ' (x) = 2 sen (x) cos (x)= 0 ⇒ 2 sen (x) cos (x) = 0
La ecuación será igual a 0 cuando sen(x)= 0 ó cos(x) = 0
sen (x) = 0 ⇔ x = 0 , x = π
cos(x) = 0 ⇔ x = π/2
Estudiaremos sólo aquellos puntos que estén dentro del período de la función: (0, π/2) , (π/2, π)
| Intervalo | (0 , π/2) | (π/2 , π) |
|---|---|---|
| Punto de prueba | f ' ( π/3) > 0 | f ' (3π/4) < 0 |
| Signo de f ' (x) | + | - |
| Monotonía | Crece | Decrece |
Por el apartado anterior sabemos que los puntos críticos o puntos que anulan a la derivada primera son x = 0 , x = π y x = π/2 , vamos a determinar a través de la segunda derivada si se tratan de máximos o mínimos.
Hallamos la derivada segunda: f '' (x) = 2( cos(x) cos(x) - sen(x) sen(x) ) = 2( cos2x - sen2x )
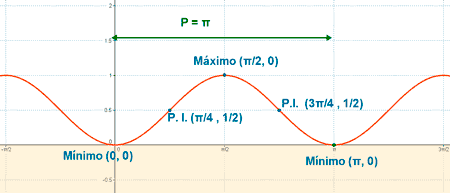
• f '' (0) = 2 > 0 ⇒ Hay un mínimo en x = 0 ⇒ f(0) = 0 ⇒ Min (0, 0)
• f '' (π) = 2 > 0 ⇒ Hay un mínimo en x = π ⇒ f(π) = 0 ⇒ Min (π, 0)
• f '' (π/2) = -2 < 0 ⇒ Hay un máximo en x = π/2 ⇒ f(π/2) = 1 ⇒ Min (π/2, 1)
Curvatura y puntos de inflexión
Se halla la derivada segunda, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
f '' (x) = 2( cos2x - sen2x ) = 0 ⇒ cos2x = sen2x ⇒ cos x = sen x ⇒ x = π/4 , x = π/4 + π/2 = 3π/4
Por tanto, los puntos que anulan la ecuación son: x = π/4 , x = 3π/4
Tenemos que estudiar los siguientes intervalos: (0, π/4) , ( π/4, 3π/4) , (3π/4 , π):
| Intervalo | (0, π/4) | ( π/4, 3π/4) | (3π/4 , π) |
|---|---|---|---|
| Punto de prueba | f '' ( π/6) > 0 | f '' ( π/2) < 0 | f '' (2π/3) > 0 |
| Signo de f '' (x) | + | - | + |
| Curvatura | Concava (∪) | Convexa (∩) | Concava (∪) |
La función es cóncava hacia arriba o simplemente concava en (0, π/4) ∪ (3π/4 , π) y concava hacia abajo o convexa en el intervalo ( π/4, 3π/4) .
Punto de inflexión
Por el apartado anterior sabemos que los puntos que anulan a la derivada segunda son x = π/4 , x = 3π/4 y vamos a determinar a través de la tercera derivada si se tratan de un punto de inflexión.
f ''' (x) = 2[ - 2cos(x)sen(x) - 2sen(x)cos(x) ] = 2[ - 4cos(x)sen(x) ] = - 8cos(x)sen(x)
f ''' (π/4) = - 4 ≠ 0 ⇒ x = π/4 es la abscisa del punto de inflexión ⇒ f(π/4) = 1/2 ⇒ Punto inflexión ( π/4, 1/2)
f ''' (3π/4) = 4 ≠ 0 ⇒ x = 3π/4 es la abscisa del punto de inflexión ⇒ f(3π/4) = 1/2 ⇒ Punto inflexión (3π/4, 1/2)


 INICIO
INICIO
