Ejercicios de derivadas II
Calcula la derivada de las siguientes funciones:
1) y = loga (2x3 + 7)
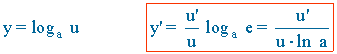
u = 2x3 + 7 → u' = 2·3·x3-1 + 0 = 6x2
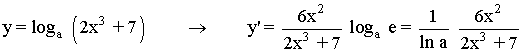
![]()

u = 5x + 1 → u' = 5
![]()
3) y = x4 Ln x
Aplicamos la regla del producto para derivadas:
![]()
4) y = x3 Ln (4 - x)
Aplicamos la regla del producto para derivadas:
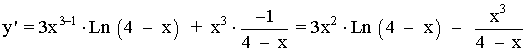
5) y = Ln3(5x)
Aplicamos la fórmula de la derivada para funciones potenciales:
y = un y' = n · un-1 · u'
u = Ln(5x) → u' = 5/5x
![]()
![]()
Aplicamos la regla del cociente para derivadas:
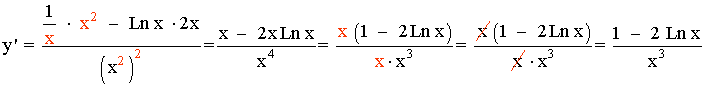
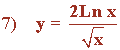
Aplicamos la regla del cociente para derivadas:
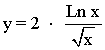
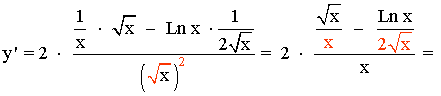
Aplicamos m.c.m. de los denominadores marcados en color rojo:
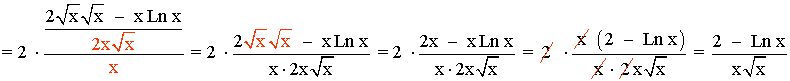
Calcula la derivada de las siguientes funciones, aplicando si fuese necesario las propiedades de los logaritmos:
![]()
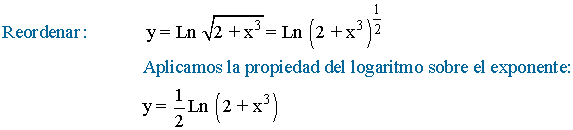
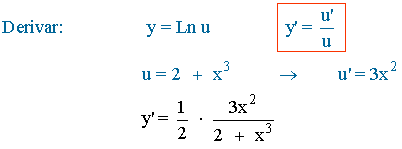
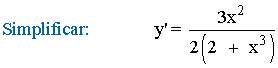
También podríamos haberla calculado aplicando directamente la fórmula de la derivada para el logaritmo neperiano. El resultado es el mismo.
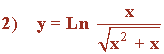
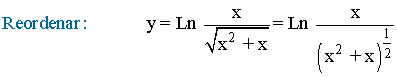
Aplicamos la propiedad del logaritmo sobre el cociente:
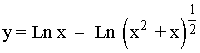
Aplicamos la propiedad del logaritmo sobre el exponente:
![]()
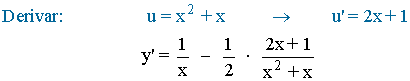
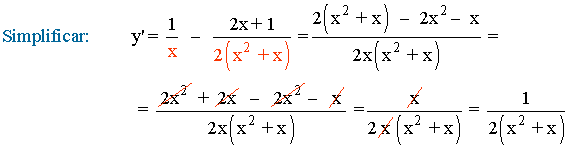
![]()
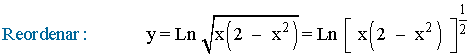
Aplicamos la propiedad del logaritmo sobre el exponente:
![]()
Aplicamos la propiedad del logaritmo sobre el producto:
![]()
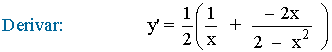
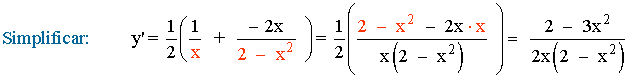
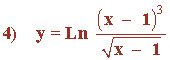
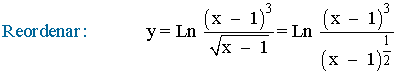
Aplicamos la propiedad del logaritmo sobre el cociente:
![]()
Aplicamos la propiedad del logaritmo sobre el exponente:
![]()
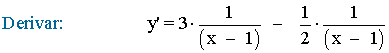
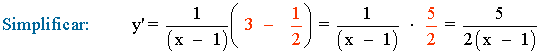
Calcula la derivada de las siguientes funciones trigonométricas:
1) y = 5 sen (3x2)
y = sen u y' = u' · cos u
u = 3x2 → u' = 3·2·x2-1 = 6x
y = 5 sen(3x2) → y' = 5·(6x) · cos (3x2) = 30x cos(3x2)
2) y = cos(2x5 - 3x + 7)
y = cos u y' = - u' · sen u
u = 2x5 - 3x + 7 → u' = 2·5·x4 - 3 = 10x4 - 3
y = cos(2x5 - 3x + 7) → y' = - (10x4 - 3) · sen (2x5 - 3x + 7)
3) y = π tg √ x
y = tg u y' = u' (1 + tg2u)
u = √x → u' = 1/(2√x)
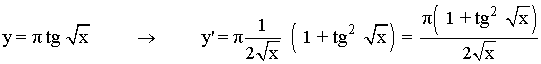
4) y = 3 cos2(5x - 1)
u = cos(5x - 1) → u' = - 5 sen (5x - 1)
y = 3 cos2(5x - 1) → y' = 3·2·cos2-1(5x-1) · [ -5 sen(5x - 1) ] = - 30 cos (5x - 1) sen(5x - 1)
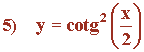
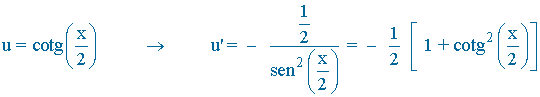
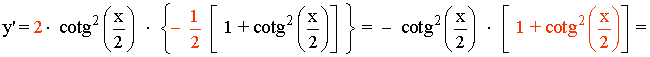
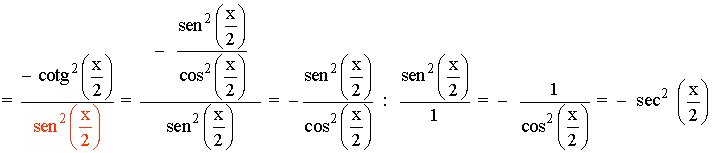
![]()
y = sec u y' = u' · sec u · tg u
u = 6x3 → u' = 6·3·x3-1 = 18x2
y = sec (6x3) → y' = 18x2 · sec (6x3) · tg (6x3)
7) y = x2 · cos (3x)
Aplicamos la fórmula de la derivada para el producto:
y' = 2x · cos(3x) + x2 · [ - 3 sen(3x) ] = 2x cos(3x) - 3x2 sen (3x)
![]()
Aplicamos la fórmula de la derivada para el cociente:
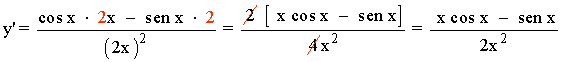
9) y = Ln cos(2x)
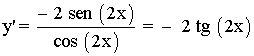
10) y = ex · cos(x/2)
Aplicamos la fórmula de la derivada para el producto:
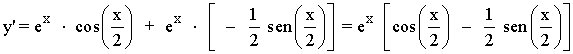
11) y = cotg (3 - 5x3)

u = 3 - 5x3 → u' = - 15x2
Calcula la derivada de las siguientes funciones trigonométricas:
1) y = arc sen (3x2 - 1)

u = 3x2 - 1 → u' = 6x
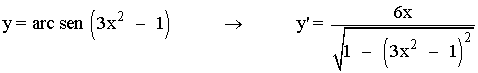
2) y = arc tg (√x)

u = √x → u' = 1/(2√x)
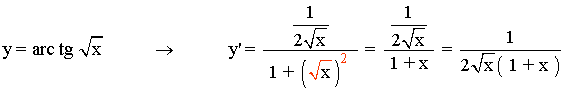
3) y = arc tg x · Ln(x2- x3)
Aplicamos la fórmula de la derivada para el producto:
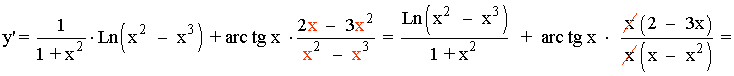
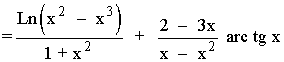
![]()
Aplicamos la fórmula de la derivada para el cociente: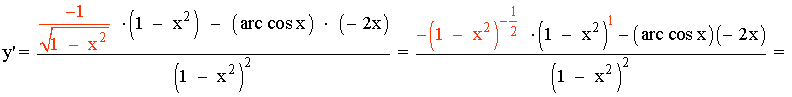
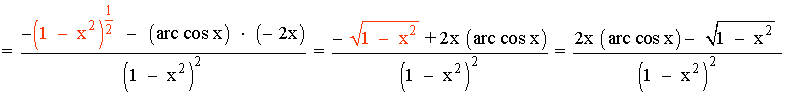
También podríamos simplificar la derivada efectuando la diferencia con el m.c.m. de los denominadores.
Calcula la derivada de las siguientes funciones potenciales exponenciales:
![]()
Esta función tiene la variable x tanto en el exponente como en la base.
En primer lugar vamos a aplicar logaritmo neperiano a ambos lados de la igualdad: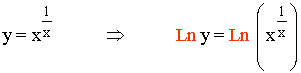
En segundo lugar aplicamos la propiedad de los logaritmos sobre el exponente:
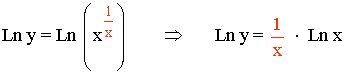
Derivamos a ambos lados de la igualdad: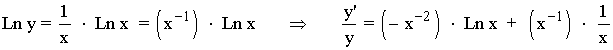
Despejamos y' , después sustituimos por el valor de y , que es la función original: y = x1/x
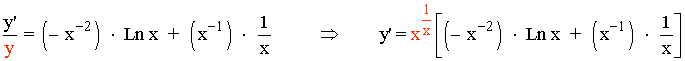
Simplificamos el resultado: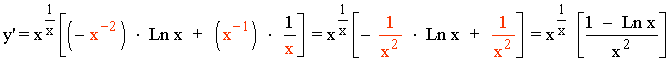
![]()
Esta función tiene la variable x tanto en el exponente como en la base.
En primer lugar vamos a aplicar logaritmo neperiano a ambos lados de la igualdad:
![]()
En segundo lugar aplicamos la propiedad de los logaritmos sobre el exponente:
![]()
Derivamos a ambos lados de la igualdad:
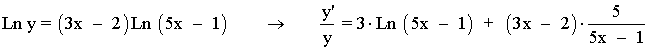
Despejamos y' , después sustituimos por el valor de y , que es la función original:
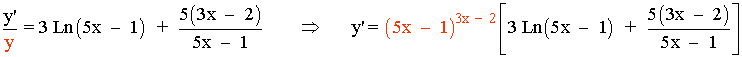
![]()
Pasamos la función a forma potencial:![]()
Esta función tiene la variable x tanto en el exponente como en la base.
En primer lugar vamos a aplicar logaritmo neperiano a ambos lados de la igualdad:
![]()
En segundo lugar aplicamos la propiedad de los logaritmos sobre el exponente:
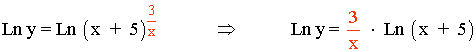
Derivamos a ambos lados de la igualdad: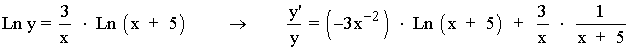
Simplificamos:
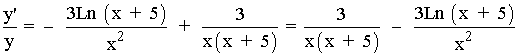
Despejamos y' , después sustituimos por el valor de y , que es la función original:
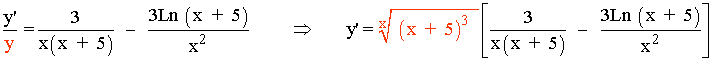
Calcula la derivada de las siguientes funciones:
1) y = xsen x
Esta función tiene la variable x tanto en el exponente como en la base.
En primer lugar vamos a aplicar logaritmo neperiano a ambos lados de la igualdad:
![]()
En segundo lugar aplicamos la propiedad de los logaritmos sobre el exponente:
![]()
Derivamos a ambos lados de la igualdad:
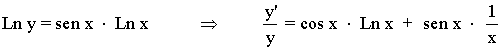
Despejamos y' , después sustituimos por el valor de y , que es la función original: y = xsen x
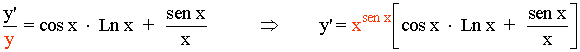
2) y = (tg x)sen x
Esta función tiene la variable x tanto en el exponente como en la base.
En primer lugar vamos a aplicar logaritmo neperiano a ambos lados de la igualdad:
![]()
En segundo lugar aplicamos la propiedad de los logaritmos sobre el exponente:
![]()
Derivamos a ambos lados de la igualdad:
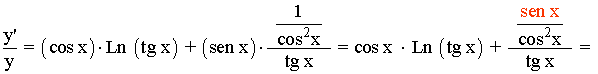
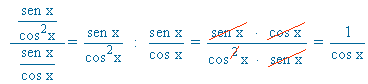
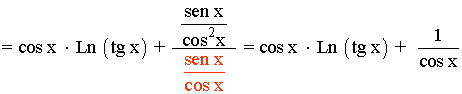
Despejamos y' , después sustituimos por el valor de y , que es la función original:
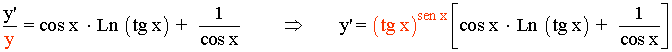
3) y = (cos x)cos x
Esta función tiene la variable x tanto en el exponente como en la base.
En primer lugar vamos a aplicar logaritmo neperiano a ambos lados de la igualdad:
![]()
En segundo lugar aplicamos la propiedad de los logaritmos sobre el exponente:
![]()
Derivamos a ambos lados de la igualdad:
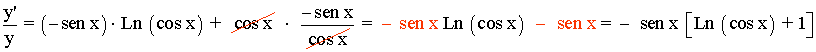
Despejamos y' , después sustituimos por el valor de y , que es la función original:
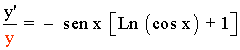
![]()


 INICIO
INICIO