Ejercicios resueltos de paralelas, perpendiculares y haces de rectas
1-a ) Calcula la recta que es paralela al eje X y que pasa por el punto A ( 2 , 3 ). Escribe su ecuación vectorial.
1-b ) Calcula la recta que es paralela al eje Y y que pasa por el punto A ( -1 , 3 ). Escribe su ecuación parametrica.
1-c ) Escribe las ecuaciones parametricas de la recta que pasa por el punto A ( 5 , -1 ) y es paralela a la siguiente recta:
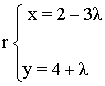
2-a ) Calcular la ecuación general de la recta que pasa por A ( -2 , 5 ) y es paralela al vector v ( -1 , 3 )
2-b ) Averigua la ecuación general de la recta que pasa por el punto P ( 2 , -2 ) y cuya pendiente es m = -3
2-c ) Halla la ecuación general de la recta perpendicular a 2x + y - 3 = 0 que pasa por el punto A ( 1 , 1 )
3 ) Halla las ecuaciones paramétricas de la recta que pasa por A ( 2 , -1 ) y es perpendicular a la recta de ecuación 3x-2y+1=0
4 ) calcula la ecuación de la recta perpendicular a r que pase por el punto P en los siguientes casos:
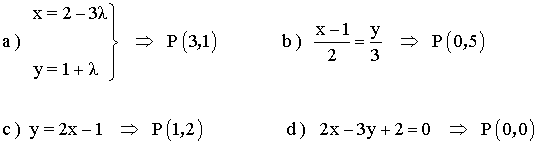
5 ) Calcular:
a ) ¿ Cómo sería la ecuación de una recta cualquiera que pase por el punto ( 2 , -1 ) ?
b ) ¿ Cúal de todas estas pasarían por el punto ( 0 , 3 ) ?
c ) ¿ Cúal de ellas sería paralela a la recta x + 2y = 5 ?
6 ) Calcular la ecuación de las saiguientes rectas:
a ) Paralela a x + y - 2 = 0 y que pasa por el punto (0 , 2 )
b ) Paralela al eje de abcisas y que pasa por el punto ( 2 , -2 )
c ) Paralela al eje de ordenadas y que pasa por el putno ( 2 , -2 )
d ) Paralela a la recta 2x - y + 8 = 0 y que pase por el origen de coordenadas.
e ) Paralela a la siguiente recta:
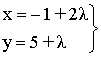
f ) Paralela a la bisectriz del primer cuadrante y que tiene ordenada en el origen igual a 2.
7 ) Calcula la ecuación de las siguientes rectas:
a ) Perpendicular a 3x + 2y - 5 = 0 y que pase por el punto ( 3 , 3 ).
b ) Perpendicualr al eje de abcisas y que pase por el punto ( -2 , 7 ).
c ) Perpendicualr al eje de ordenadas y que pasa por el punto ( 5 , -1 ).
d ) Perpendicular a 3x - 6y + 2 = 0 y que pase por el origen de ordenadas.
e ) Perpendicular a la siguinte recta:
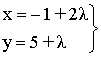
f ) Perpendicular al segmento AB con A ( 0 , 2 ) y B ( 3 , 1 ) y que pase por ( -3 , 3 ).
8 ) Determina el valor de t para que las siguientes rectas sean perpendiculares:
r: 3x - 4y + 12 = 0
s: tx + 8y - 15 = 0
9 -a ) Halla la ecuación general de la recta paralela a 3x - 2y + 5 = 0 y pasa por el punto A(-2, 1) .
9 -b ) Halla la ecuación general de la recta perpendicular a 2x + y - 3 = 0 que pasa por el punto A ( 1 , 1 ) .
10 ) Calcular:
a ) El haz de rectas que pasa por el punto A ( 3 , -1 ) en forma continua.
b ) ¿ Cúal de las rectas del haz es paralela a la recta 3x - y = 2 ?
c ) ¿ Cúal de las rectas del haz pasa por el punto medio del segmento de extremos A ( 4 , -1 ) y B ( 0 , -5 ) ?
11 ) Consideremos el haz de rectas de centro ( 2 , -1 )
a ) Escribe la ecuación de este haz de rectas.
b ) Halla la ecuación de la recta de este haz que pasa por el punto ( -1 , 2 )
c ) ¿ Cúal de las rectas del haz es paralela a x + 2y = 0 ?
d ) Halla la recta del haz cuya distancia al origen es igual a 2
12 ) Hallar la recta del haz de centro ( 2 , 3/2) y que pasa por ( 0 , 3 ).
13 ) Las rectas r : x - 3y + 2 = 0 y s : x + 2y - 1 = 0 forman parte de un haz. ¿ Cúal es la recta de ese haz que pasa por el punto ( 3 , -2 ) ?
14 ) Calcula la ecuación del haz determinado por las rectas secantes r : 2x + 3y = 0 y s : 3x - y = 0 y halla la recta de este haz que tiene pendiente m = - 1 / 3
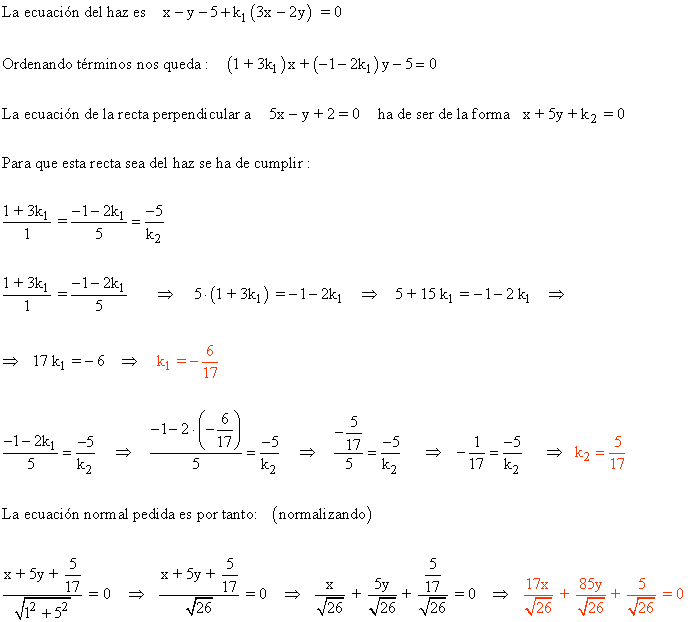
15 ) Halla la ecuación del haz determinado por las rectas secantes r : x - y = 5 y s : 3x - 2y = 0 e indica la ecuación normal de la recta del haz que es perpendicular a la recta t : 5x - y + 2 = 0
1- a ) Calcula la recta que es paralela al eje X y que pasa por el punto A ( 2 , 3 ). Escribe su ecuación vectorial.

1-b ) Calcula la recta que es paralela al eje Y y que pasa por el punto A ( -1 , 3 ). Escribe su ecuación parametrica.

1-c ) Escribe las ecuaciones parametricas de la recta que pasa por el punto A ( 5 , -1 ) y es paralela a la siguiente recta:
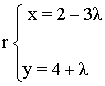

2-a ) Calcular la ecuación general de la recta que pasa por A ( -2 , 5 ) y es paralela al vector v ( -1 , 3 )

2-b ) Averigua la ecuación general de la recta que pasa por el punto P ( 2 , -2 ) y cuya pendiente es m = -3
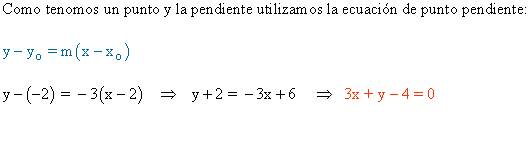
2-c ) Halla la ecuación general de la recta perpendicular a 2x + y - 3 = 0 que pasa por el punto A ( 1 , 1 )

También podemos hallar la ecuación mediante las pendientes:
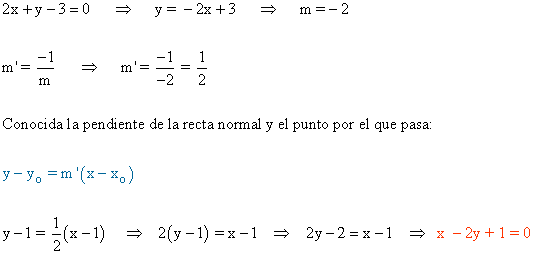
3 ) Halla las ecuaciones paramétricas de la recta que pasa por A ( 2 , -1 ) y es perpendicular a la recta de ecuación 3x-2y+1=0

4 ) calcula la ecuación de la recta perpendicular a r que pase por el punto P en los siguientes casos:
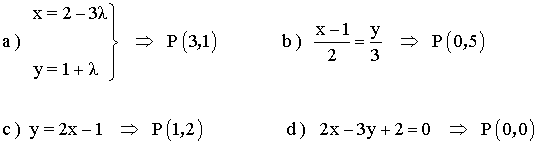
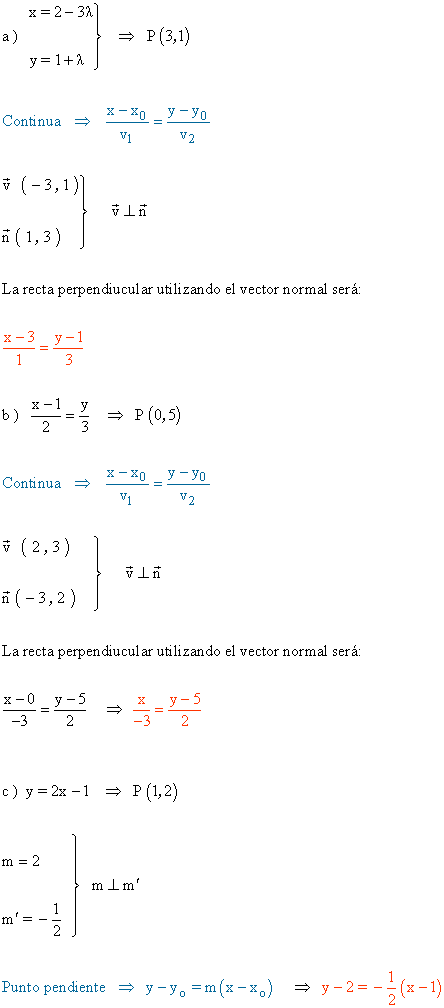

5 ) Calcular:
a ) ¿ Cómo sería la ecuación de una recta cualquiera que pase por el punto ( 2 , -1 ) ?
b ) ¿ Cúal de todas estas pasarían por el punto ( 0 , 3 ) ?
c ) ¿ Cúal de ellas sería paralela a la recta x + 2y = 5 ?
a ) ¿ Cómo sería la ecuación de una recta cualquiera que pase por el punto ( 2 , -1 ) ?
![]()
b ) ¿ Cúal de todas estas pasarían por el punto ( 0 , 3 ) ?

c ) ¿ Cúal de ellas sería paralela a la recta x + 2y = 5 ?
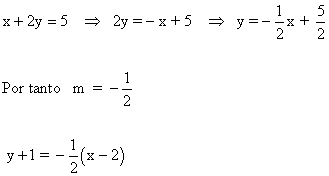
6 ) Calcular la ecuación de las saiguientes rectas:
a ) Paralela a x + y - 2 = 0 y que pasa por el punto (0 , 2 )
b ) Paralela al eje de abcisas y que pasa por el punto ( 2 , -2 )
c ) Paralela al eje de ordenadas y que pasa por el putno ( 2 , -2 )
d ) Paralela a la recta 2x - y + 8 = 0 y que pase por el origen de coordenadas.
e ) Paralela a la siguiente recta:
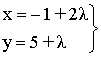
f ) Paralela a la bisectriz del primer cuadrante y que tiene ordenada en el origen igual a 2.

7 ) Calcula la ecuación de las siguientes rectas:
a ) Perpendicular a 3x + 2y - 5 = 0 y que pase por el punto ( 3 , 3 ).
b ) Perpendicualr al eje de abcisas y que pase por el punto ( -2 , 7 ).
c ) Perpendicualr al eje de ordenadas y que pasa por el punto ( 5 , -1 ).
d ) Perpendicular a 3x - 6y + 2 = 0 y que pase por el origen de ordenadas.
e ) Perpendicular a la siguinte recta:
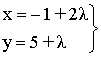
f ) Perpendicular al segmento AB con A ( 0 , 2 ) y B ( 3 , 1 ) y que pase por ( -3 , 3 ).
Fórmulas a emplear:
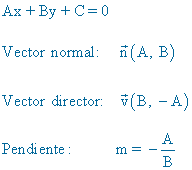
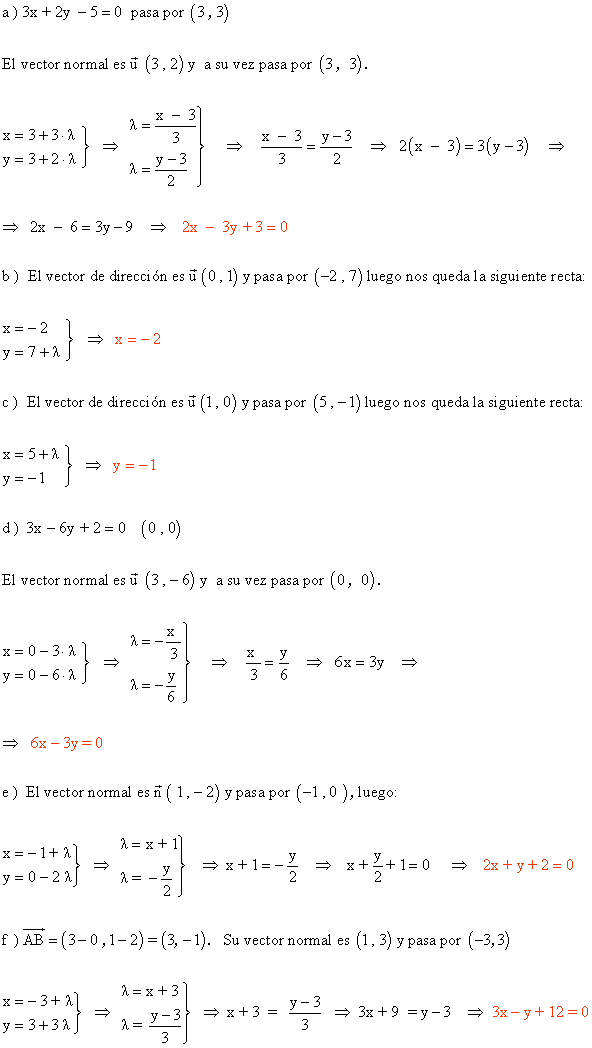
8 ) Determina el valor de t para que las siguientes rectas sean perpendiculares:
r: 3x - 4y + 12 = 0
s: tx + 8y - 15 = 0
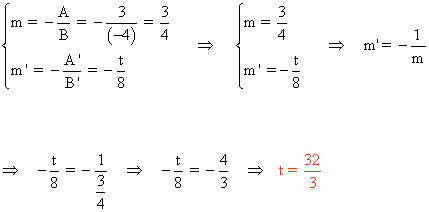
9 -a ) Halla la ecuación general de la recta paralela a 3x - 2y + 5 = 0 y pasa por el punto A(-2, 1) .
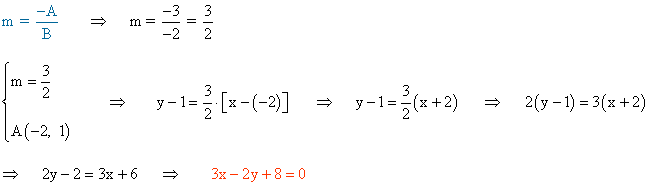
También podemos hallarla de la siguiente manera:
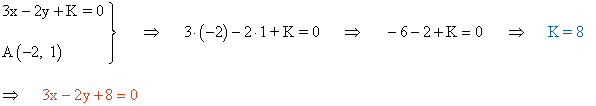
9 -b ) Halla la ecuación general de la recta perpendicular a 2x + y - 3 = 0 que pasa por el punto A ( 1 , 1 ) .
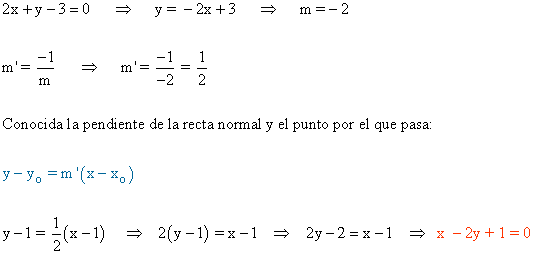
También podemos calcular la ecuación utilizando el vector normal a la recta:

10 ) Calcular:
a ) El haz de rectas que pasa por el punto A ( 3 , -1 ) en forma continua.
b ) ¿ Cúal de las rectas del haz es paralela a la recta 3x - y = 2 ?
c ) ¿ Cúal de las rectas del haz pasa por el punto medio del segmento de extremos A ( 4 , -1 ) y B ( 0 , -5 ) ?
a ) El haz de rectas que pasa por el punto A ( 3 , -1 ) en forma continua.
![]()
b ) ¿ Cúal de las rectas del haz es paralela a la recta 3x - y = 2 ?
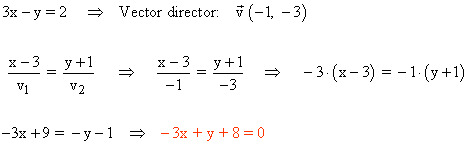
c ) ¿ Cúal de las rectas del haz pasa por el punto medio del segmento de extremos A ( 4 , -1 ) y B ( 0 , -5 ) ?
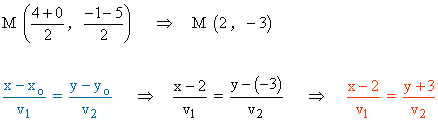
11 ) Consideremos el haz de rectas de centro ( 2 , -1 )
a ) Escribe la ecuación de este haz de rectas.
b ) Halla la ecuación de la recta de este haz que pasa por el punto ( -1 , 2 )
c ) ¿ Cúal de las rectas del haz es paralela a x + 2y = 0 ?
d ) Halla la recta del haz cuya distancia al origen es igual a 2
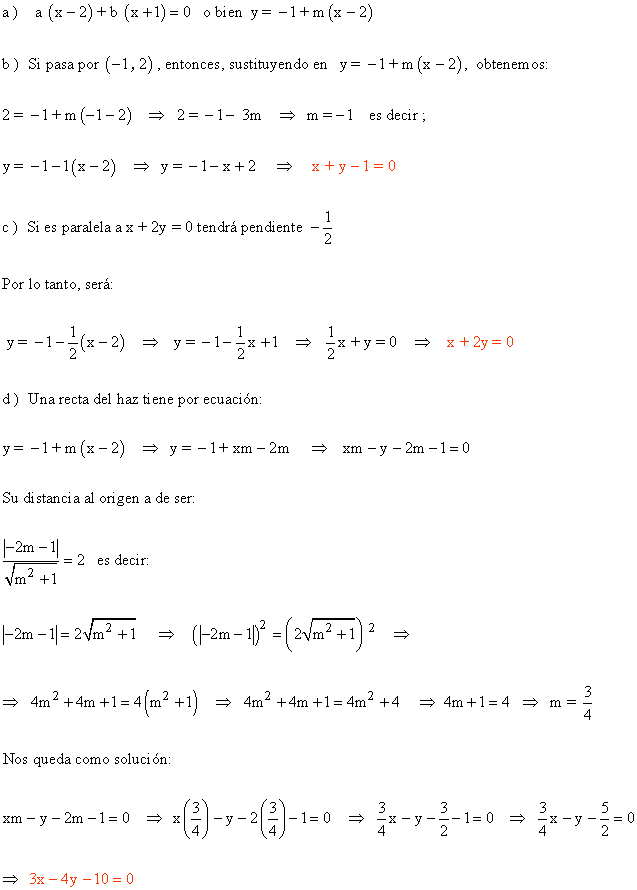
12 ) Hallar la recta del haz de centro ( 2 , 3/2) y que pasa por ( 0 , 3 ).
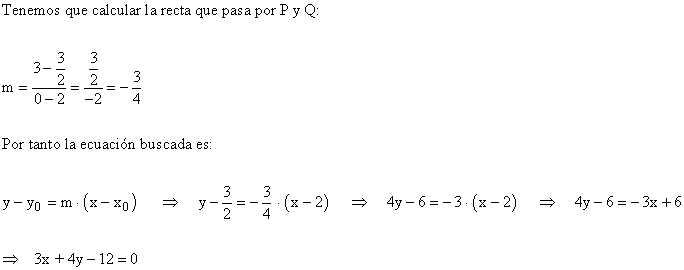
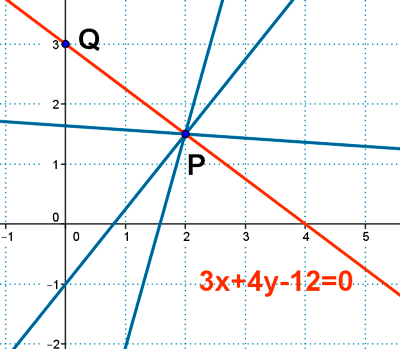
13 ) Las rectas r : x - 3y + 2 = 0 y s : x + 2y - 1 = 0 forman parte de un haz. ¿ Cúal es la recta de ese haz que pasa por el punto ( 3 , -2 ) ?

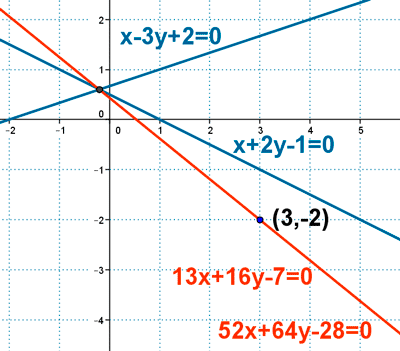
14 ) Calcula la ecuación del haz determinado por las rectas secantes r : 2x + 3y = 0 y s : 3x - y = 0 y halla la recta de este haz que tiene pendiente m = - 1 / 3
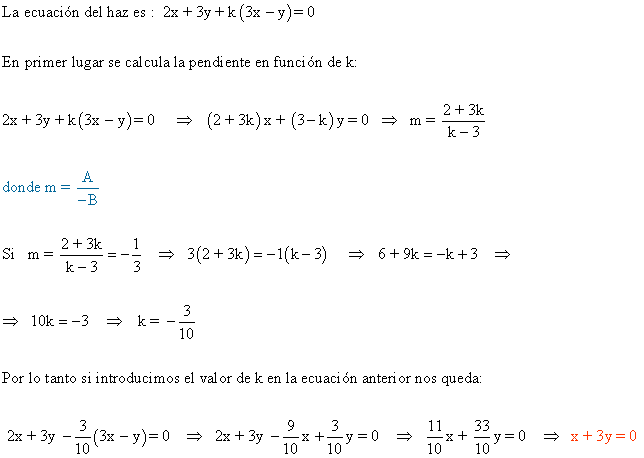
15 ) Halla la ecuación del haz determinado por las rectas secantes r : x - y = 5 y s : 3x - 2y = 0 e indica la ecuación normal de la recta del haz que es perpendicular a la recta t : 5x - y + 2 = 0


 INICIO
INICIO