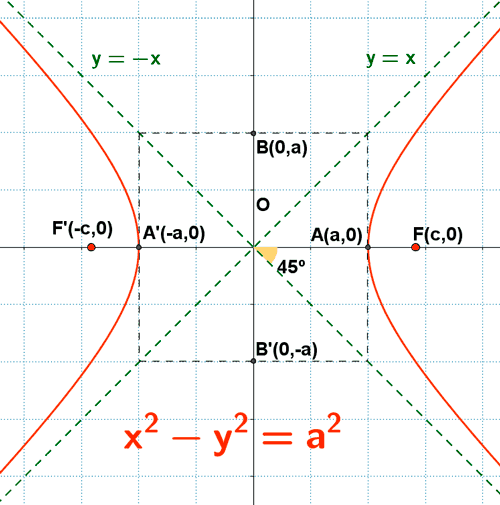
Hipérbola equilátera
Una hipérbola equilátera es una hipérbola centrada en el origen y con los focos en el eje OX, donde la longitud del semieje real coincide con la del semieje imaginario, es decir, a = b .
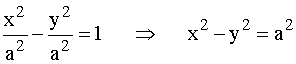
Esta expresión es la ecuación reducida de la hipérbola equilátera.

Ejemplo:
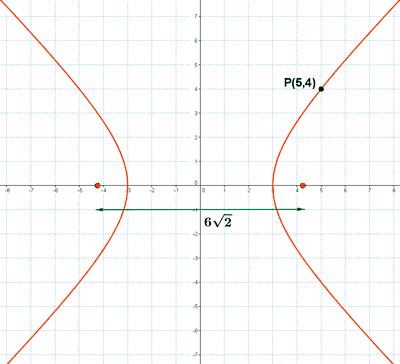
Hallar la hipérbola equilátera de distancia focal 2c = 6√2. ¿Pertenece el punto P(5, 4) a dicha hipérbola?
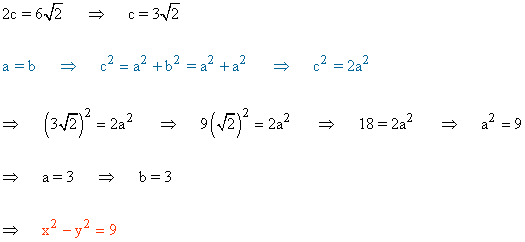
A continuación comprobamos si el punto P(5, 4) pertenece a la hipérbola:
![]()
Como satisface la ecuación, el punto pertenece a la hipérbola.
Ecuación de una hipérbola equilátera referida a su asíntota
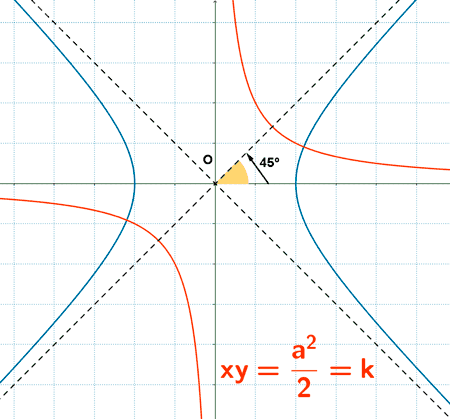
En general, la ecuación de una hipérbola equilátera referida a su asíntota, es de la forma:
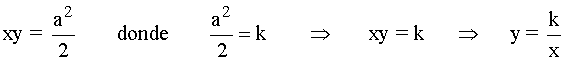
Esta ecuación es la resultante de realizar un giro de 45º de la hipérbola equilátera, de forma que sus asíntotas se han convertido en unos nuevos ejes de coordenadas.
Ejemplo:
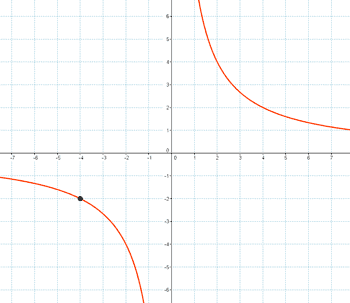
Hallar la hipérbola equilátera referida a sus asíntotas y que pasa por el punto P(-4, -2).
![]()


 INICIO
INICIO

