Binomio de Newton
La fórmula del binomio de Newton sirve para calcular las potencias de un binomio utilizando números combinatorios.
Desarrollo de (a + b)m
![]()
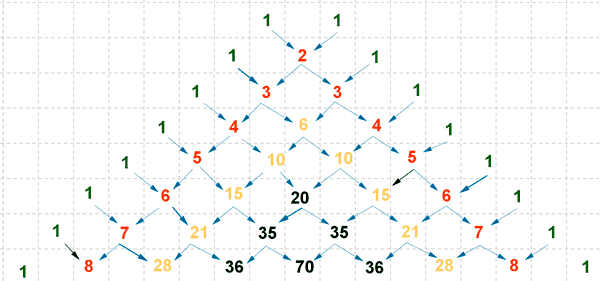
Triangulo de Tartaglia o triángulo de Pascal
Para hallar los coeficientes del binomio de Newton nos podemos ayudar del triángulo de Tartaglia o triángulo de Pascal:
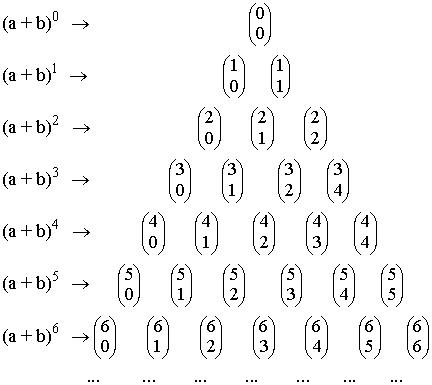
Ejemplo de binomio de Newton:
Obtén el polinomio que resulta de desarrollar la expresión (2 + 3x3)4.
Aplicamos la fórmula del binomio de Newton (a + b)n.
Donde a = 2 , b = 3x3 y n =4
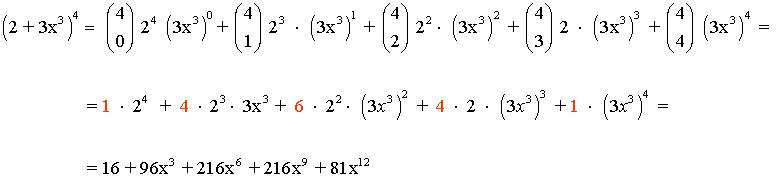
Donde los coeficientes marcados en rojo corresponden con los del triángulo de Tartaglia o triángulo de Pascal.
1) (x - 3)5
Aplicamos la fórmula del binomio de Newton (a + b)n.
Donde a = x , b = -3 y n =5
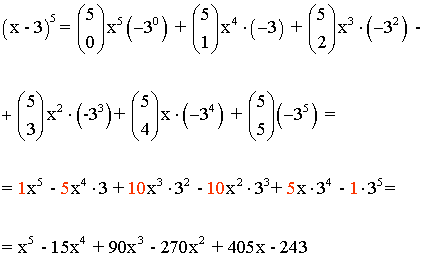
Donde los coeficientes marcados en rojo corresponden con los del triángulo de Tartaglia o triángulo de Pascal.
Término general
El término general es el que ocupa el lugar n + 1.
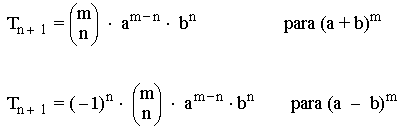
Ejemplo de término general:
Hallar el octavo término del desarrollo de (3x + 2y)15
Calculamos el término octavo utilizando la fórmula para a = 3x , b = 2y , n = 7 m =15
![]()
El desarrollo del número 15 sobre 7 es el siguiente:
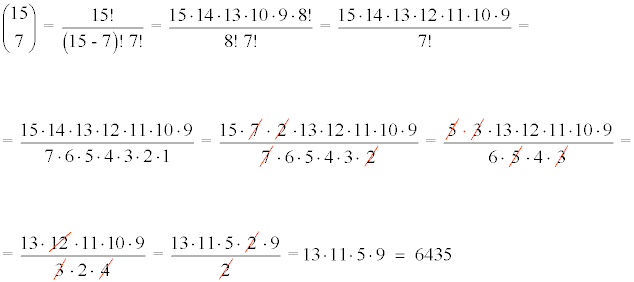
Por lo tanto el octavo término se expresa de la siguiente manera:
![]()


 INICIO
INICIO

