Infinitésimos
Dada una función f(x) decimos que es un infinitésimo en un entorno de un punto a (o en las proximidades de un punto a) si se cumple que:
![]()
Decimos que x3 es un infinitésimo en x = 0 pues:
![]()
Pero decimos que 1 + x3 no es un infinitésimo en x = 0 puesto que:
![]()
Las siguientes funciones:
f(x) = sen x , f(x) = 1 - cos x , f(x) = tg x , f(x) = x , f(x) = x2 + x
son infinitésimos en un entorno del cero, ya que cumplen en todos los casos que:
![]()
Las siguientes funciones:
f(x) = x2 - 1 , f(x) = sen(x - 1) , f(x) = (x3 - 1)/x2 , f(x) = ln(2 - x)
son infinitésimos en un entorno del uno , ya que cumplen en todos los casos que:
![]()
Las funciones:
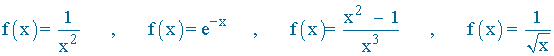
son infinitésimos para x tendiendo hacia + ∞ ya que cumplen en todos los casos que:
![]()
Infinitésimos equivalentes
Dadas las funciones f(x) y g(x) infinitésimos en un entorno de a , decimos que son infinitésimos equivalentes en un entorno del punto a si se cumple:
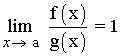
1) La función f(x) = x y g(x) = sen x son infinitésimos equivalentes en un entorno de cero, puesto que se cumple:
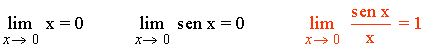
2) La función f(x) = x y g(x) = tg x son infinitésimos equivalentes en un entorno del cero, puesto que se cumple:
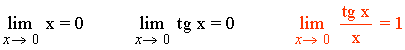
3) La función f(x) = 1 - cos x y g(x) = x2/2 son infinitésimos equivalentes en un entorno del cero, puesto que se cumple:
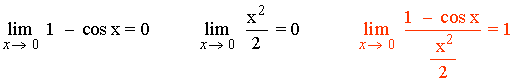
4) La función f(x) = arc sen x y g(x) = x son infinitésimos equivalentes en un entorno del cero, puesto que se cumple:
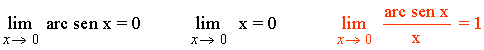
5) La función f(x) = arc tg x y g(x) = x son infinitésimos equivalentes en un entorno del cero, puesto que se cumple:
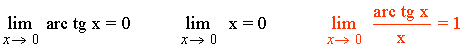
6) La función f(x) = ln (1 + x) y g(x) = x son infinitésimos equivalentes en un entorno del cero, puesto que se cumple:
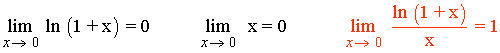
7) La función f(x) = ex - 1 y g(x) = x son infinitésimos equivalentes en un entorno del cero, puesto que se cumple:
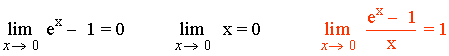
Aplicaciones de infinitésimos equivalentes
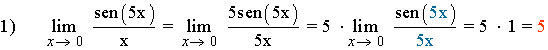
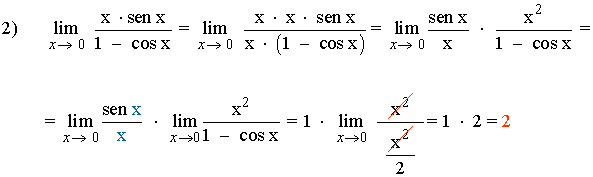


 INICIO
INICIO

