Cálculo de límites de funciones: x → + ∞
Operaciones con expresiones infinitas
| Suma | 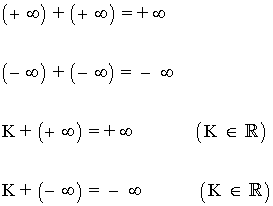 |
|---|---|
| Producto | 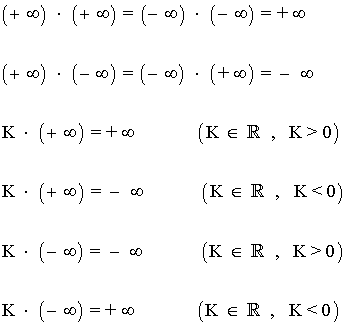 |
| Cociente | 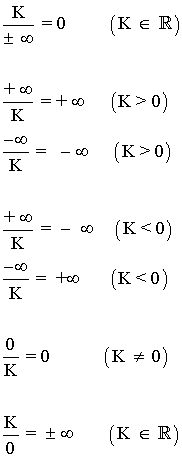 |
| Potencia | 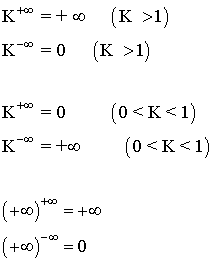 |
Resumen de límites determinados
Resumen de límites indeterminados
Límites de funciones elementales
Hallar los siguientes límites elementales:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
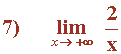
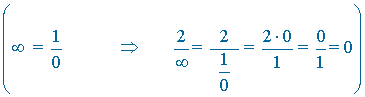
![]()
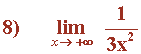
![]()
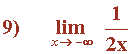
![]()

![]()
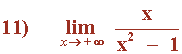
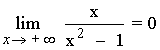
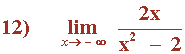
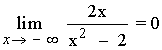
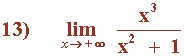
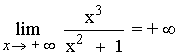
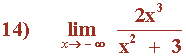
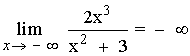
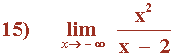
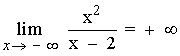
Hallar los siguientes límites:
![]()
El término con el exponente de mayor grado tiene coeficiente positivo, por tanto:
![]()
![]()
El término con el exponente de mayor grado tiene coeficiente negativo, por tanto:
![]()
![]()
El término con el exponente de mayor grado tiene coeficiente positivo, por tanto:
![]()
![]()
El término con el exponente de mayor grado tiene coeficiente negativo, por tanto:
![]()
Hallar los siguientes límites:
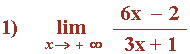
Vamos a intentar resolverlo primero de la siguiente forma:
![]()
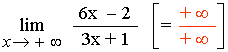
El resultado es una indeterminación.
Para resolver este límite dividimos numerador y denominador entre la x de mayor exponente, que en nuestro caso es : x
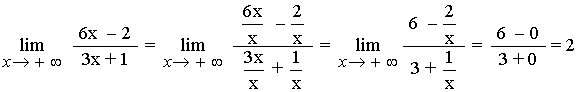
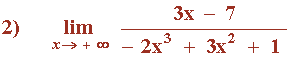
El grado del denominador es mayor que el del numerador, por tanto el límite vale:
![]()
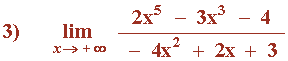
El grado del numerador es mayor que el del denominador, por tanto el límite vale:
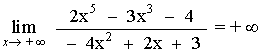
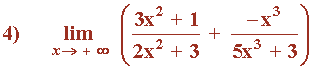
Podemos aplicar la siguiente propiedad de los límites:
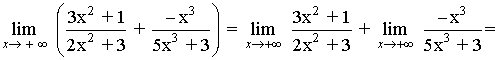
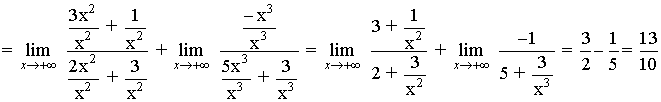
Hallar los siguientes límites:
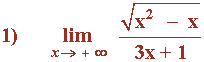
Aunque parece que el exponente de mayor grado es 2, observamos que dicho término está bajo la influencia de una raíz cuadrada, por tanto su grado podríamos decir que es: (x2) 1/2 = x1
Por tanto, el mayor grado de la función es 1. Tenemos que dividir numerador y denominador por x .
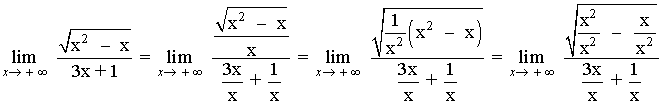
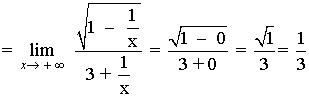
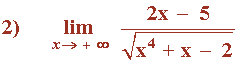
Dividimos numerador y denominador por la x de mayor exponente: x2
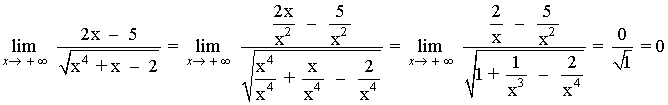
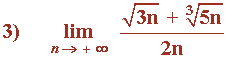
Observamos que los grados del numerador son: n1/2 , n1/3
El grado del denominador es mayor que el del numerador: 1> 1/2 y 1 > 1/3
Por tanto, dividimos numerador y denominador por el término de mayor exponente: n
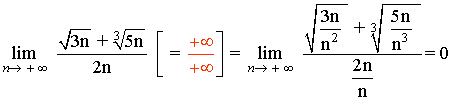
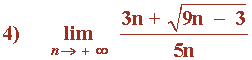
El exponente de mayor grado es 1.
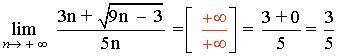
Hallar los siguientes límites:
![]()
Multiplicamos y dividimos por el conjugado de la función:
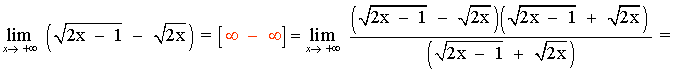
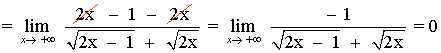
![]()
Multiplicamos y dividimos por el conjugado de la función:
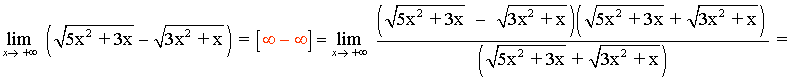
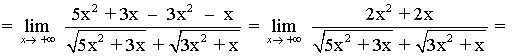
El término de mayor grado es x2, por tanto, dividimos numerador y denominador por x2 y calculamos el límite:
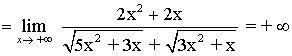
![]()
Multiplicamos y dividimos por el conjugado de la función:
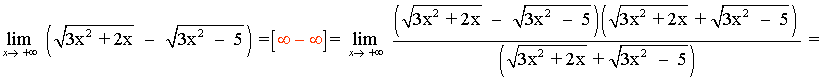
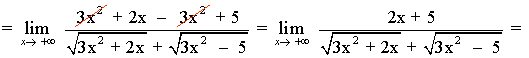
Aunque puede parecer que el término de mayor grado es x2, dicho término está bajo la influencia de una raíz cuadrada, por tanto: (x2)1/2 = x
Luego el término de mayor grado es x , así que dividimos numerador y denominador por x y calculamos el límite:
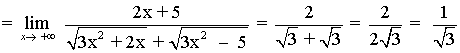
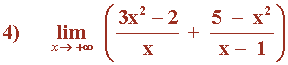
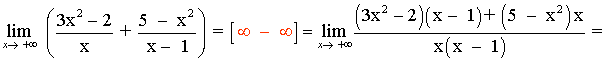
![]()
El numerador es de mayor grado que el denominador, por tanto:
![]()
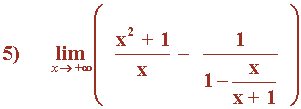
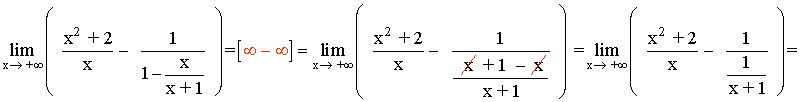
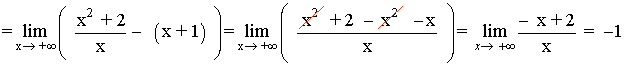
Hallar los siguientes límites:
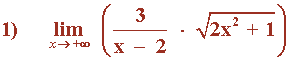
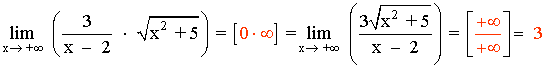
Observamos que el término de mayor grado, tanto en el numerador como en el denominador, es x .
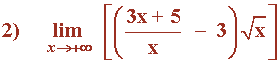
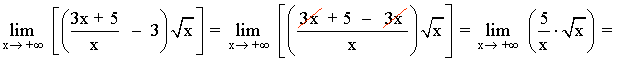
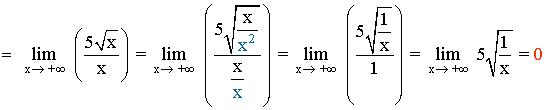
Observamos que el término de mayor grado es x , por tanto, dividimos numerador y denominador por x .


 INICIO
INICIO