Cálculo de límites de funciones: x → a
Operaciones con expresiones infinitas
| Suma | 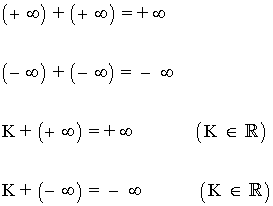 |
|---|---|
| Producto | 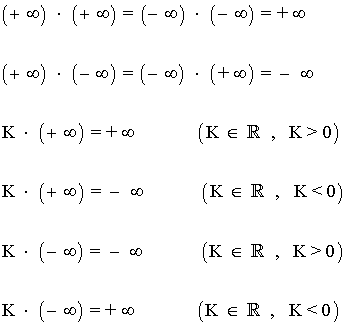 |
| Cociente | 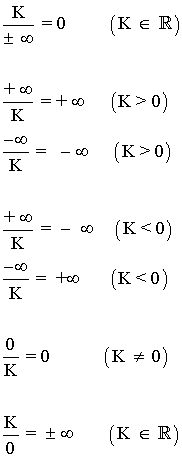 |
| Potencia | 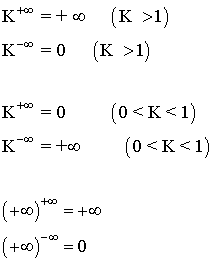 |
Resumen de límites determinados
Resumen de límites indeterminados
Límites de funciones elementales
Hallar los siguientes límites elementales:
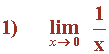
Tenemos que calcular los límites laterales.
El límite será + ∞ ó - ∞ , o no existirá (porque sus límites laterales no coincidan).
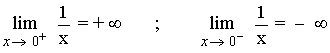
Como los límites laterales no coinciden, el límite no existe.
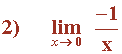
Tenemos que calcular los límites laterales.
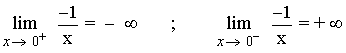
Como los límites laterales no coinciden, el límite no existe.
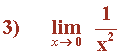
Tenemos que calcular los límites laterales.
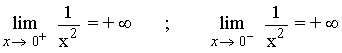
Como los límites coinciden:
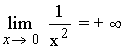
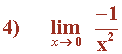
Tenemos que calcular los límites laterales.
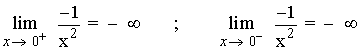
Como los límites coinciden:
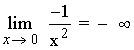
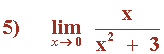
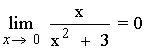
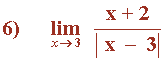
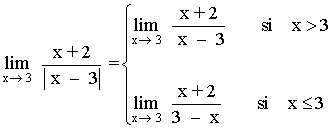
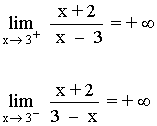
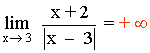
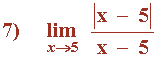
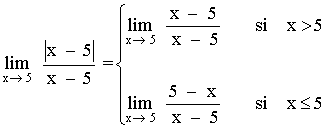
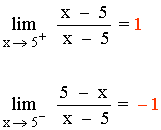
Los límites laterales son distintos, por tanto el límite cuando x → 5 no existe.
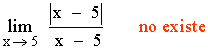
Hallar los siguientes límites:
![]()
![]()
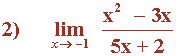
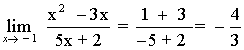
![]()
![]()
![]()
![]()
No tiene sentido calcular el límite puesto que la función no está definida en el punto x = 1 .
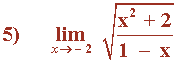
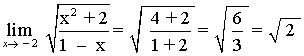
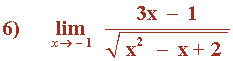
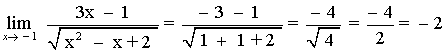
![]()
![]()
![]()
![]()
![]()
![]()
Hallar los siguientes límites de funciones trigonométricas:
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
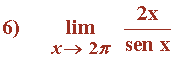
![]()
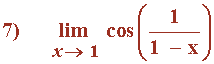
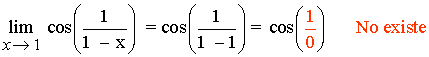
![]()
![]()

![]()
![]()
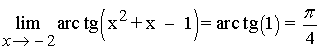
Hallar los siguientes límites:
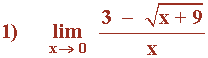
Multiplicamos y dividimos por el conjugado de la función:
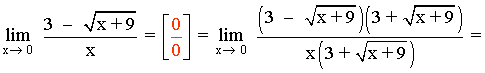
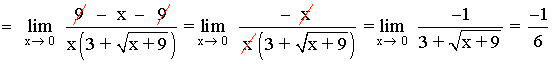
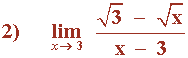
Multiplicamos y dividimos por el conjugado de la función:
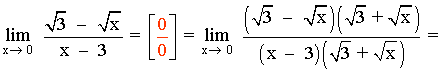
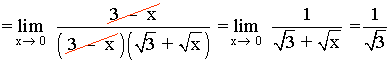
Hallar los siguientes límites factorizando el numerador y denominador de la función:
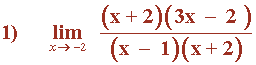
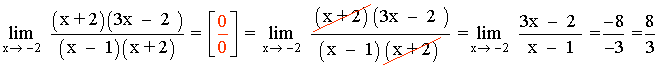
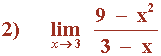
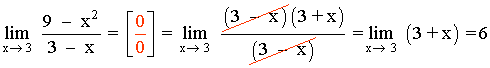
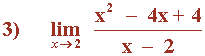
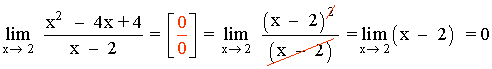
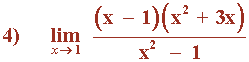
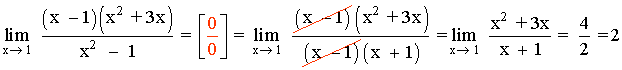
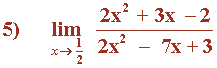
Observamos que x = 1/2 es raíz tanto del numerador como del denominador:
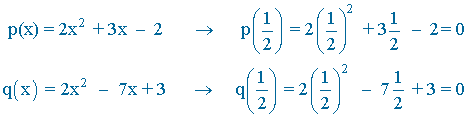
Por tanto, si efectuásemos el límite tendríamos una indeterminación:
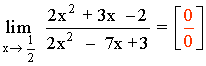
Para resolver el límite factorizamos numerador y denominador mediante Ruffini:
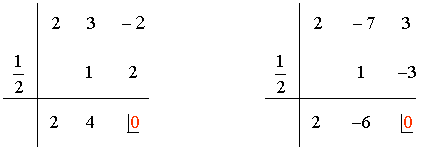
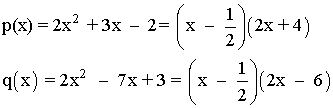
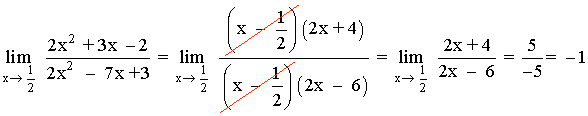
También podríamos hacer la factorización resolviendo las dos ecuaciones de segundo grado p y q .
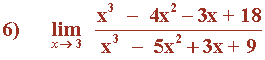
Observamos que x = 3 es raíz tanto del numerador como del denominador:
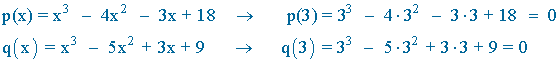
Por tanto, si efectuásemos el límite tendríamos una indeterminación:
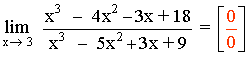
Para resolver el límite factorizamos numerador y denominador mediante Ruffini:

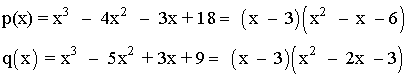
Intentamos resolver el límite:
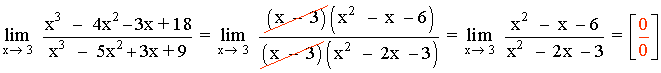
Como vuelve a ser una indeterminación, seguimos factorizando:

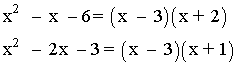
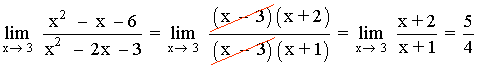
También podríamos hacer la factorización resolviendo las dos ecuaciones de segundo grado .
Hallar los siguientes límites:
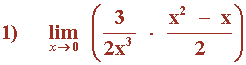
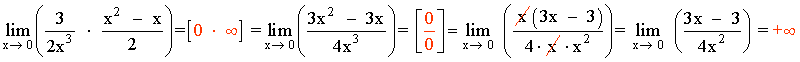
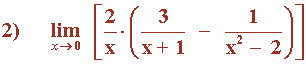
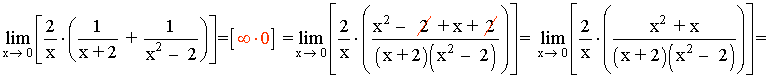
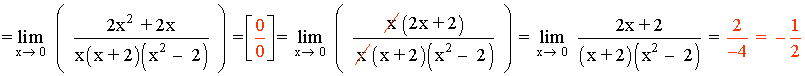


 INICIO
INICIO