Funciones polinómicas de segundo grado
Las funciones polinómicas de segundo grado se llaman funciones cuadráticas y son del tipo:
![]()
donde a ≠ 0 , siendo su gráfica una parábola.
Las características generales de las funciones polinómicas de segundo grado son:
1) El dominio de las funciones cuadráticas es R.
2) Tiene un eje de simetría cuya fórmula es:
![]()
3) El vértice de la parábola es:
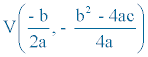
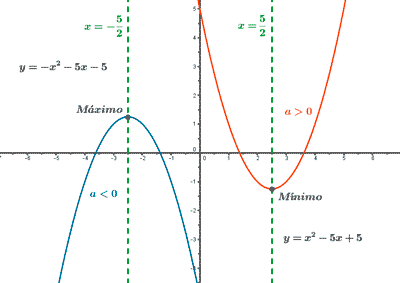
4) Corta al eje X en dos puntos, uno o ninguno, según el número de raíces reales de ax2 + bx + c = 0 .
5) Corta el eje Y en el punto (0, c) .
6) El vértice es un mínimo si a > 0 y un máximo si a < 0 .
7) Es concava si a > 0 y convexa si a < 0 .
8) Al aumentar a en valor absoluto, la parábola se hace más estrecha.
Tipos de funciones cuadráticas
En una función cuadrática f(x) = ax2 + bx + c , con a ≠ 0 .
Si b = 0 y c = 0
La función f(x) = ax2 tiene su vértice en el punto (0, 0) y su eje de simetría es el eje Y.
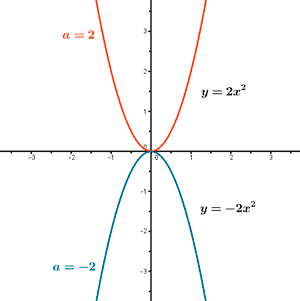
Si b = 0 y c ≠ 0
La función f(x) = ax2 + c tiene su vértice en el punto (0, c) y su eje de simetría es el eje Y.
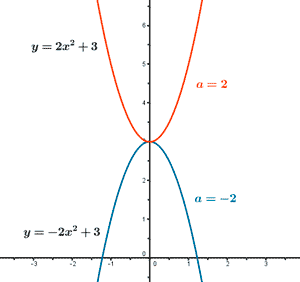
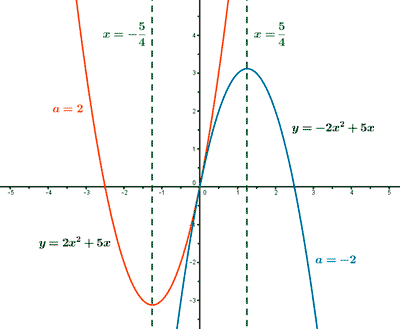
Si b ≠ 0 y c = 0
La función f(x) = ax2 + bx tiene su vértice y su eje de simetría en:
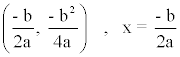
Representa graficamente la función: f(x) = x2 - 5x + 6
1) Puntos de corte con los ejes:
Para x = 0 tenemos que f(0) = 6 luego el punto de corte con el eje Y es (0, 6) .
Para y = 0 tenemos que 0 = x2 - 5x + 6 así que resolvemos la ecuación de segundo grado:
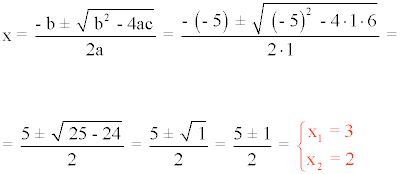
Por lo tanto, los puntos de corte con el eje X son (2, 0) y (3, 0) .
2) Eje de simetría :
![]()
3) Vértice de la parábola:
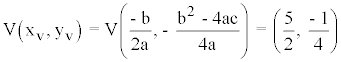
También podemos hacer yv = f(5/2)
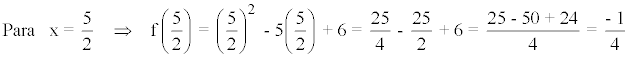
3) Máximos o mínimos:
Como a > 0 entonces tenemos un mínimo, que coincide con el vértice.
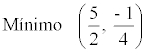
4) Crecimiento o decrecimiento:
Como a > 0, tenemos que la función es decreciente en el intervalo (- ∞, 5/2) y creciente en el intervalo (5/2, + ∞).
5) Concavidad o convexidad:
Como a > 0 la función es concava en todo su dominio.
6) Tabla de valores:
Construimos una tabla de valores con los puntos de corte con los ejes, el vértice y otros puntos alrededor de él.
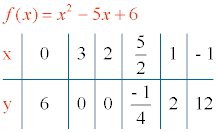
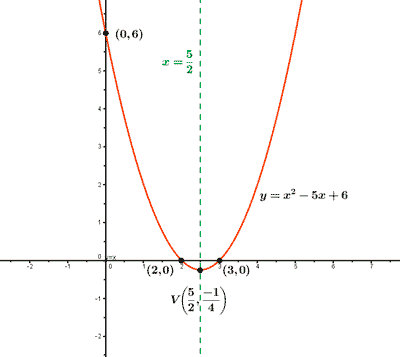
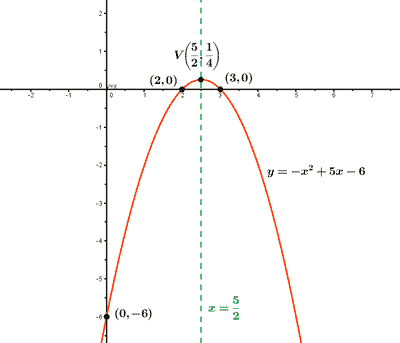
Representa graficamente la función: f(x) = - x2 + 5x - 6
1) Puntos de corte con los ejes:
Para x = 0 tenemos que f(0) = - 6 luego el punto de corte con el eje Y es (0, - 6) .
Para y = 0 tenemos que 0 = - x2 + 5x - 6 así que resolvemos la ecuación de segundo grado, siendo sus raíces x = 2 y x = 3.
Por lo tanto, los puntos de corte con el eje X son (2, 0) y (3, 0) .
2) Eje de simetría :
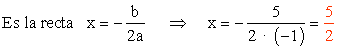
3) Vértice de la parábola:
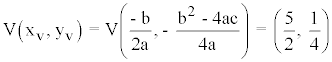
También podemos hacer yv = f(5/2)
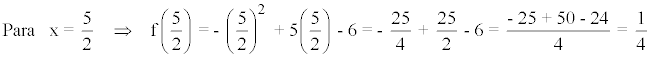
3) Máximos o mínimos:
Como a < 0 entonces tenemos un máximo, que coincide con el vértice.
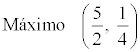
4) Crecimiento o decrecimiento:
Como a < 0, tenemos que la función es creciente en el intervalo (- ∞, 5/2) y decreciente en el intervalo (5/2, + ∞).
5) Concavidad o convexidad:
Como a < 0 la función es convexa en todo su dominio.
6) Tabla de valores:
Construimos una tabla de valores con los puntos de corte con los ejes, el vértice y otros puntos alrededor de él.
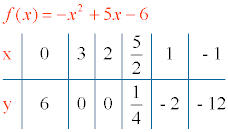


 INICIO
INICIO

