Ejercicios de dominio de funciones.
- 1. Polinómicas
- 2. Racionales
- 3. Irracionales I
- 4. II
- 5. III
- 6. Logarítmicas
- 7. Exponenciales
- 8. Trigonométricas
Halla el dominio de las siguientes funciones:
1) f(x) = 5x
Es una función polinómica, por tanto: Dom (f) = R
2) f(x) = 4x3 +3x2 - 1
Es una función polinómica, por tanto: Dom f(x) = R
3) f(x) = (x - 5)2
Es una función polinómica, por tanto: Dom f(x) = R
![]()
Es una función racional, por tanto, el dominio de f está formado por todos los números reales,
excepto por aquellos que anulan el denominador.
x3 = 0 ⇔ x = 0
Dom (f) = R - {0}
5) El área de un cuadrado de lado x , es A = x2 .
El dominio de A es: x > 0
Pues la longitud de los lados de un figura geométrica tiene que ser un número real positivo.
Hallar el dominio de las siguientes funciones racionales:
![]()
El dominio de f está formado por todos los números reales,
excepto por aquellos que anulan el denominador.
3x - 2 = 0 ⇔ x = 2/3
Dom (f) = R - {2/3}
![]()
El dominio de f está formado por todos los números reales,
excepto por aquellos que anulan el denominador.
x2 - 4 = 0 ⇔ x2 = 4 ⇔ x = ±√4 ⇔ x = ±2
Dom (f) = R - { 2, - 2}
![]()
El dominio de f está formado por todos los números reales,
excepto por aquellos que anulan el denominador.
x2 + 1 = 0 ⇔ x2 = - 1 ⇔ x = ±√-1 ∉ R
Dom (f) = R
![]()
El dominio de f está formado por todos los números reales,
excepto por aquellos que anulan el denominador.
x2 + x - 2 = 0
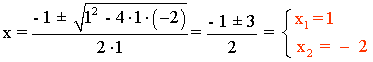
Dom (f) = R - { 1, - 2}
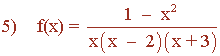
El dominio de f está formado por todos los números reales,
excepto por aquellos que anulan el denominador.
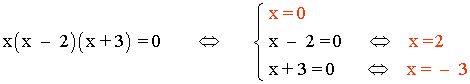
Dom (f) = R - { 0, 2, - 3}
![]()
Para ver su dominio calculamos los puntos que anulan al denominador:
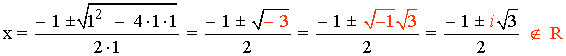
Los valores que anulan el denominador son complejos, por tanto, la función está bien definida para todo número real.
Luego: Dom(f) = R
Hallar el dominio de las siguientes funciones irracionales:
![]()
El índice es par, por tanto,
el dominio de la función f serán aquellos valores reales tales que: x - 3 ≥ 0
x - 3 ≥ 0 ⇔ x ≥ 3
Dom (f) = [3 , ∞)
![]()
El índice es impar, por tanto,
el dominio de la función f será el dominio de la función polinómica.
Dom f(x) = R
![]()
El índice es par, por tanto,
el dominio de la función f serán aquellos valores reales tales que: x2 + 2 ≥ 0
Para cualquier valor de x se cumple que: x2 + 2 ≥ 0
Dom (f) = R
![]()
El índice es par, por tanto,
el dominio de f serán aquellos valores reales tales que: x2 - 5x ≥ 0
x2 - 5x = 0 ⇔ x(x - 5) = 0 ⇔ x = 0 ó x = 5
Estudiamos el signo en los intervalos: (-∞ , 0) , (0, 5) , (5 , ∞)
• (-∞ , 0): x = - 1 ⇒ x(x - 5) = (-1)(-1 - 5) > 0
• (0 , 5): x = 1 ⇒ x(x - 5) = 1 - 5 < 0
• (5 , ∞): x = 6 ⇒ x(x - 5) = 6(6 - 5) > 0
Dom (f) = (-∞ , 0] ∪ [5 , ∞)
Incluimos los valores x = 0 y x = 5, ya que la inecuación contiene el signo = .
Hallar el dominio de las siguientes funciones irracionales:
![]()
Para ver su dominio calculamos los puntos que hacen positivo los argumentos de cada raíz:
3 + x ≥ 0 y 3 - x ≥ 0
Resolvemos el sistema de inecuaciones:
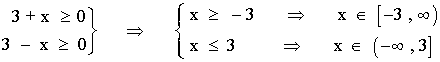
Dom(f) = (-∞ , -3] ∩ [3 , ∞) = [-3 , 3]
![]()
Para ver su dominio calculamos los puntos que hacen positivo el argumento de la raíz:
3 - 2x - x2 = 0 ⇔ x = 1 , x = -3
3 - 2x - x2 = - (x - 1)(x + 3) ≥ 0
Estudiamos el signo en los intervalos: (-∞ -3) , (-3 , 1) , (1 , ∞)
• (-∞ , -3) : x = -4 ⇒ - (-4 - 1)(-4 + 3) < 0
• (-3 , 1) : x = 0 ⇒ - (0 - 1)(0 + 3) > 0
• (1 , ∞) : x = 2 ⇒ - (2 - 1)(2 + 3) < 0
Por tanto: 3 - 2x - x2 ≥ 0 ⇔ x ∈ [- 3 , 1]
Dom(f) = [-3 , 1]
![]()
Para ver su dominio calculamos los puntos que hacen positivo el argumento de la raíz:
x2 - 6x + 9 = 0 ⇔ x = 3
x2 - 6x + 9 = (x - 3)2 ≥ 0
El argumento de la raíz siempre es mayor o igual que 0.
Por tanto, la función f está bien definida en toda la recta real.
Dom(f) = R
Hallar el dominio de las siguientes funciones irracionales:
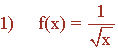
El domino de la función está formado por todos los números reales,
excepto los valores que anulan el denominador y
los que hacen el radicando menor que cero.
x > 0 ⇔ x ∈ (0 , ∞)
Dom (f) = (0, ∞)
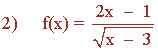
El dominio de f serán aquellos valores reales tales que x - 3 > 0.
x - 3 > 0 ⇔ x > 3 ⇔ x ∈ (3 , ∞)
Dom (f) = (3 , ∞)
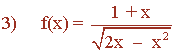
El dominio de f serán aquellos valores reales tales que 2x - x2 > 0.
2x - x2 = 0 ⇔ x (2 - x) = 0 ⇔ x = 0 ó x = 2
Estudiamos el signo en los intervalos: (-∞ , 0) , (0 , 2) , (2 , ∞)
• (-∞ , 0): x = - 1 ⇒ x(2 - x) = (-1)(2 + 1) < 0
• (0 , 2): x = 1 ⇒ x(2 - x) = 2 - 1 > 0
• (2 ,∞): x = 3 ⇒ x(2 - x) 3(2 - 3) < 0
Dom (f) = (0 , 2)
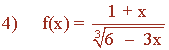
El índice es impar, por tanto, el dominio de f estará
formado por todos los números reales excepto
aquellos que anulan el denominador.
![]()
Dom (f) = R - {2}
Hallar el dominio de las siguientes funciones logarítmicas:
![]()
El dominio de f estará formado por todos los números reales tales que x - 7 > 0
x - 7 > 0 ⇔ x > 7 ⇔ x ∈ (7 , ∞)
Dom (f) = (7 , ∞)
![]()
El dominio de f estará formado por todos los números reales tales que 4 + x > 0
4 + x > 0 ⇔ x > - 4 ⇔ x ∈ (- 4 , ∞)
Dom (f) = (-4 , ∞)
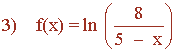
El dominio de f estará formado por todos los números reales,
excepto por aquellos que anulan el denominador y
y aquellos que hacen negativo: 8/(5 - x)
x - 5 = 0 ⇔ x = 5
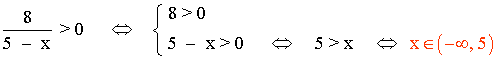
Como 5 ∉ (-∞ 5) , tenemos que: Dom (f) = (-∞ , 5)
![]()
Para ver su dominio calculamos los puntos que hacen estrictamente positivo el argumento del logaritmo:
x2 - 4 > 0 ⇔ x2 > 4 ⇔ |x| >√4 ⇔ |x| >2 ⇔ x < -2 y x > 2 ⇔ x ∈ (-∞ , -2) ∪ (2 , ∞)
Dom(f) = (-∞ , -2) ∪ (2 , ∞)
Es continua en todos los puntos de su dominio, es decir, es continua en (-∞ , -2) ∪ (2 , ∞) . Por tanto, la función no tiene puntos de discontinuidad.
SELECTIVIDAD
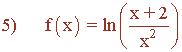
El argumento del logaritmo es racional. El único punto que anula su denominador es x = 0 .
Veamos ahora para qué puntos el argumento del logaritmo es estrictamente positivo:
![]()
También se tiene que cumplir: x ≠ 0
Dom(f) = (-2 , ∞) - {0} = (-2 , 0) ∪ (0 , ∞)
Es continua en todos los puntos de su dominio, es decir, es continua en (-2 , 0) ∪ (0 , ∞) . Por tanto, la función no tiene puntos de discontinuidad.
Halla el dominio de las siguientes funciones exponenciales:
![]()
El dominio de f será el mismo que el del exponente: 2x - 6
Por tanto: Dom (f) = R
![]()
El dominio de f estará formado por todos los números reales tales que x > 0
Dom (f) = (0 , ∞)
![]()
El dominio de f estará formado por todos los números reales tales que (x - 1) > 0
x - 1 > 0 ⇔ x > 1 ⇔ (1 , ∞)
Dom (f) = (1 , ∞)
El dominio de f estará formado por todos los números reales,
excepto aquellos que anulan el denominador del exponente: x + 1
x + 1 = 0 ⇔ x = - 1
Dom (f) = R - {-1}
Halla el dominio de las siguientes funciones trigonométricas:
1) f(x) = sen x
Dom (f) = R
2) f(x) = cos x
Dom (f) = R
3) f(x) = tg x
![]()
El dominio de f estará formado por todos los números reales,
excepto por aquellos que anulan el denominador.
![]()
De forma general, si avanzamos kπ , con k ∈ Z:
![]()
![]()
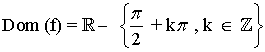


 INICIO
INICIO