Suma de matrices
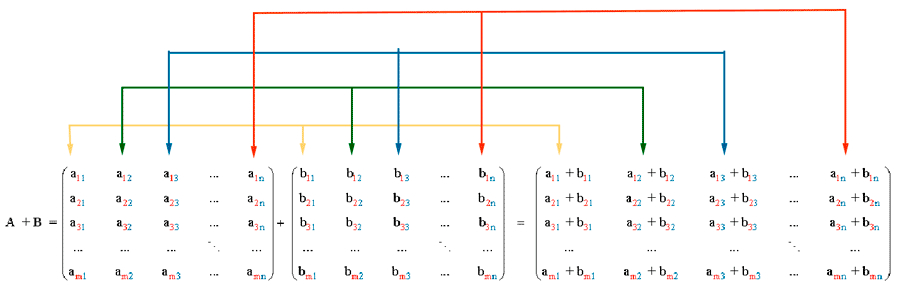
La suma de dos matrices A = ( aij ) y B = ( bij ) de la misma dimensión m × n, es otra matriz que representamos como A + B, de la misma dimensión que A y B, cuyos elementos son la suma de los elementos situados en las mismas posiciones, es decir,
A + B = (aij + bij).
Ejemplos:
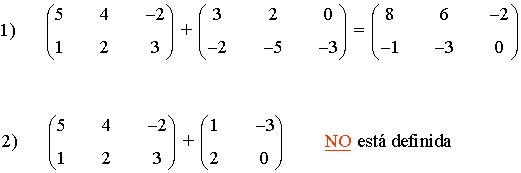
Propiedades de la suma de matrices
Dada una matriz A=(aij), la matriz opuesta de A, se representa por -A y es una matriz de la misma dimensión que A y cuyos elementos son los opuestos de los elementos de A, es decir, -A=(-aij).
- Conmutativa: A + B = B + A
- Asociativa: A + ( B + C ) = ( A + B ) + C
- Elemento Neutro: A + O = O + A = A (O es la matriz nula).
- Elemento Opuesto: A + ( -A ) = ( -A ) + A = O
- Traspuesta de la suma: ( A + B )t = At + Bt
Diferencia de dos matrices
La diferencia de dos matrices A = ( aij ) y B = ( bij ) de la misma dimensión m × n, es otra matriz que representamos como A - B , de la misma dimensión que A y B, y que se define como
A - B = A + ( -B ), es decir, A - B = ( aij - bij ).
Siendo -B la matriz opuesta de B.
Ejemplo:
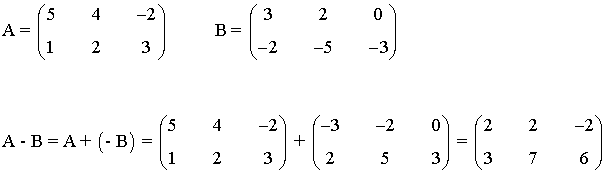


 INICIO
INICIO

