Productos de matrices

Producto de una matriz por un número real

El producto de una matriz A = ( a_ij) por un número real k es otra matriz, que representaremos por kB, de la misma dimensión que A y cuyos elementos son el producto de los mismos por k, es decir,
kA = ( ka_ij).

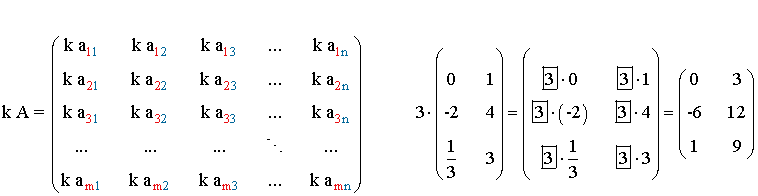
Propiedad distributiva (I): k ( A + B) = kA + kB.

Propiedad distributiva (II): (k+ h) A = kA + hA.

Propiedad asociativa mixta: k( hA ) = (kh)A (O es la matriz nula).

Elemento Neutro: 1 · A = A

Producto de una matriz fila por una matriz columna

El producto de una matriz fila por una matriz columna es un número que se obtiene multiplicando término a término los elementos y sumando los resultados.

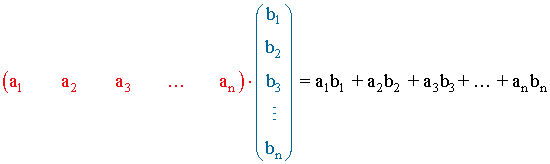
Ejemplo:

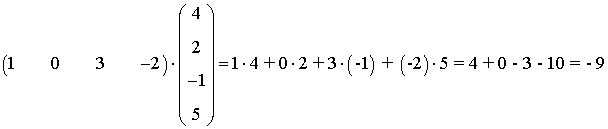
Producto de dos matrices

El producto de una matriz A = ( a_ij) de orden m × n y otra matriz A B = ( b_ij) de dimensiones n × p es una matriz C = ( c_ij) de orden m × p, de manera que cada elemento c_ij se obtiene multiplicando la fila i de A por la columna j de B, es decir:

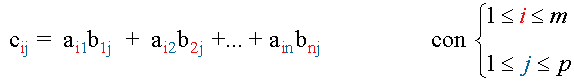
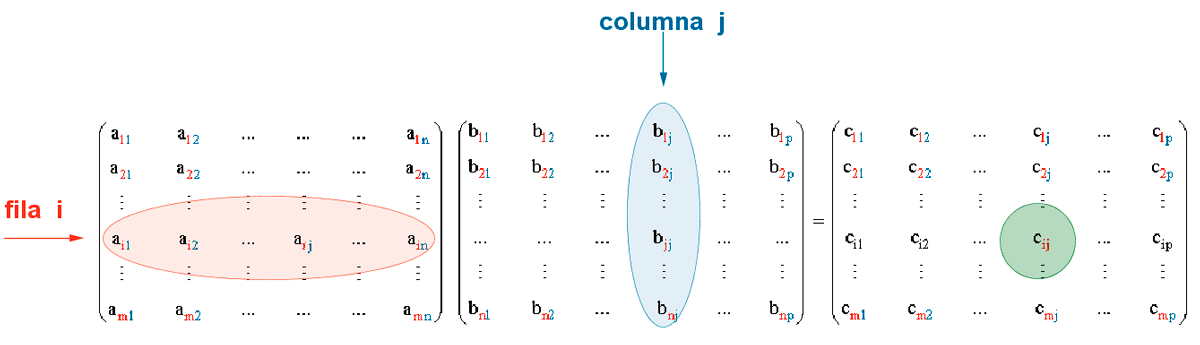
Para poder multiplicar dos matrices es obligatorio que el número de columnas de la primera coincida con el número de filas de la segunda.

Ejemplo:

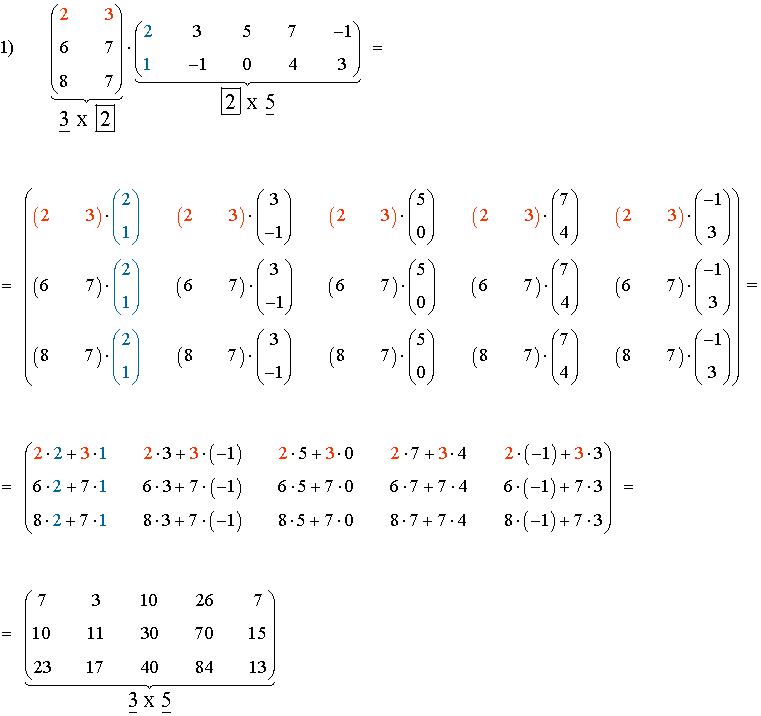
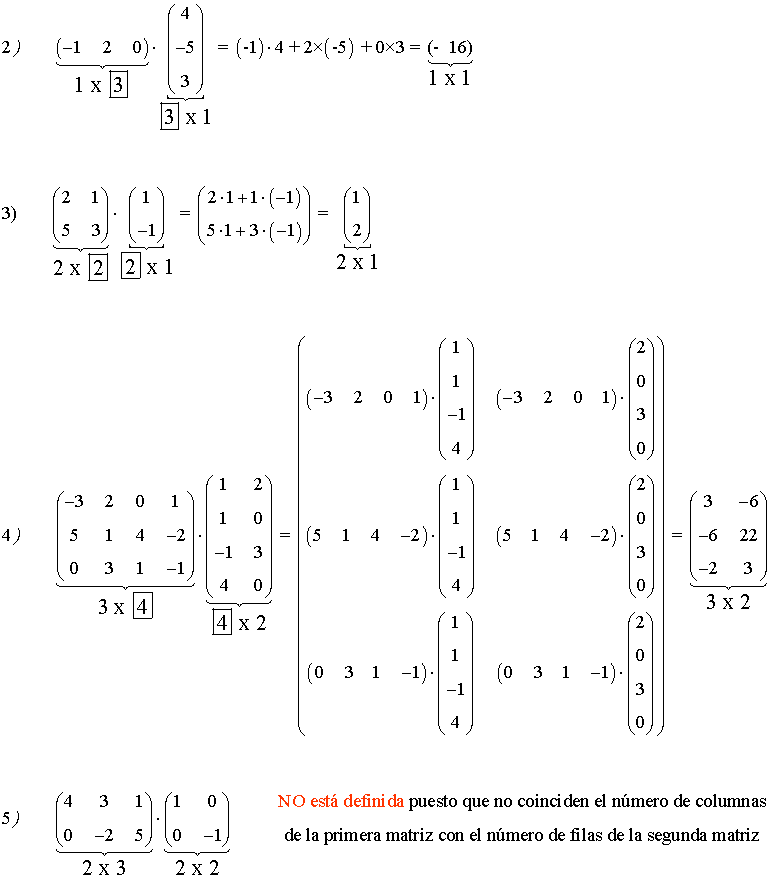
Matriz A	Matriz B	Matriz AB
3 x 2	2 x 5	3 x 5
1 x 3	3 x 1	1 x 1
2 x 2	2 x 1	2 x 1
3 x 4	4 x 2	3 x 2
2 x 3	2 x 2	No definida