Resumen de tipos de matrices
| Nombre de la matriz | Ejemplo |
|---|---|
| Matriz Fila: Es una matriz con una única fila. |
 |
| Matriz Columna: Es una matriz con una única columna. |
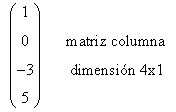 |
| Matriz nula: Matriz con todos sus elementos nulos. |
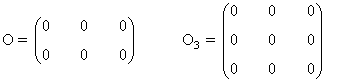 |
| Matriz rectangular: Matriz con distinto número de filas y columnas. |
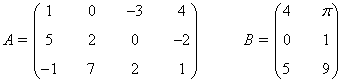 |
| Matriz traspuesta: Dada una matriz A es la matriz obtenida cambiando sus filas por sus columnas. La denotamos por At. |
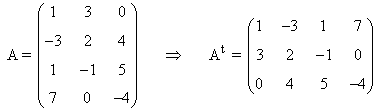 |
| Matriz Cuadrada: Matriz con tantas filas como columnas. |
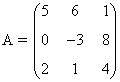 |
| Clasificación de matrices cuadradas | |
| Diagonal: Todos los elementos que no pertenecen a la diagonal principal son todos nulos. |
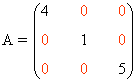 |
| Escalar: Es una matriz diagonal que tiene a todos los elementos de la diagonal principal iguales. |
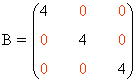 |
| Unidad: Es una matriz diagonal en que todos los elementos de la diagonal principal son iguales a 1. |
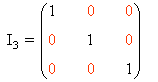 |
| Triangular superior: Todos los elementos bajo la diagonal principal son nulos. |
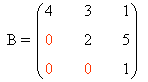 |
| Triangular inferior: Todos los elementos sobre la diagonal principal son nulos. |
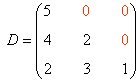 |
| Inversible o regular: Matriz que tiene inversa. |
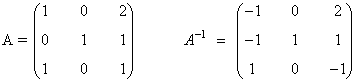 |
| Singular: Matriz que no tiene inversa |
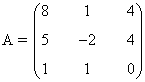 |
| Simétrica: Matriz que coincide con su traspuesta A = At |
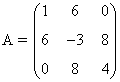 |
| Antisimétrica o hemisimétrica: Es una matriz en la que se verifica que bij = - bji A = -At Por tanto su diagonal principal está formada por ceros. |
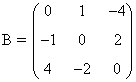 |
| Ortogonal: Es una matriz que verifica A · At=I |
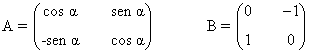 |
| Nilpotente: Es una matriz que verifica An = O |
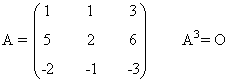 |
| Periódica: Es una matriz que verifica que An+1 = A |
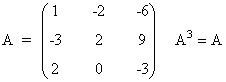 |
| Idempotente: Es una matriz que verifica que A2 = A |
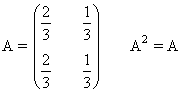 |
| Involutiva: Es una matriz que verifica que A2 = I |
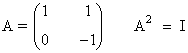 |


 INICIO
INICIO

