Ejercicios resueltos de sistemas de ecuaciones trigonométricas
1) Resuelve el siguiente sistema de ecuaciones trigonométricas:
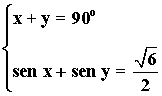
2) Resuelve el siguiente sistema de ecuaciones trigonométricas:
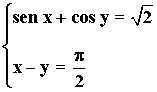
3) Resuelve el siguiente sistema de ecuaciones trigonométricas:
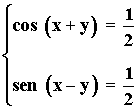
4) Resuelve el siguiente sistema de ecuaciones trigonométricas:
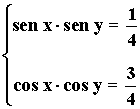
5) Resuelve el siguiente sistema de ecuaciones trigonométricas:
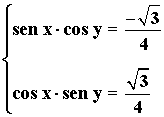
6) Resuelve el siguiente sistema de ecuaciones trigonométricas:
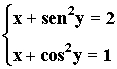
7) Resuelve el siguiente sistema de ecuaciones trigonométricas:
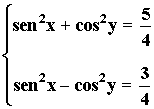
8) Resuelve el siguiente sistema de ecuaciones trigonométricas:
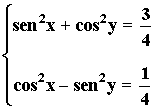
9) Resuelve el siguiente sistema de ecuaciones trigonométricas:
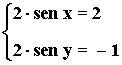
10) Resuelve el siguiente sistema de ecuaciones trigonométricas:
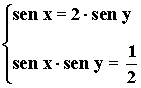
11) Resuelve el siguiente sistema de ecuaciones trigonométricas:
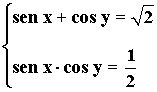
12) Resuelve el siguiente sistema de ecuaciones trigonométricas:
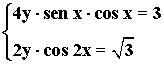
13) Resuelve el siguiente sistema de ecuaciones trigonométricas:
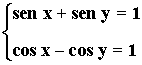
1) Resuelve el siguiente sistema de ecuaciones trigonométricas:
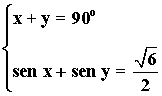
• En primer lugar, calculamos el valor de una de las incógnitas para sustituirlo en la otra ecuación:
x + y = 90o ⇒ x = 90o - y ⇒ sen x = sen (900 - y) = cos y (ángulos complementarios)
• Sustituyendo en la segunda ecuación obtenemos:
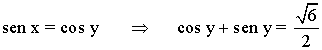
• Elevamos ambos miembros de la ecuación al cuadrado:
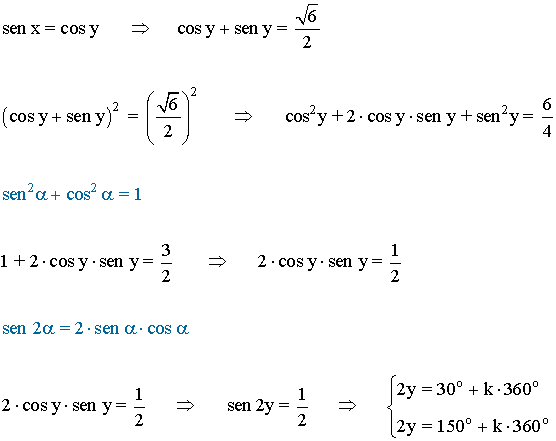
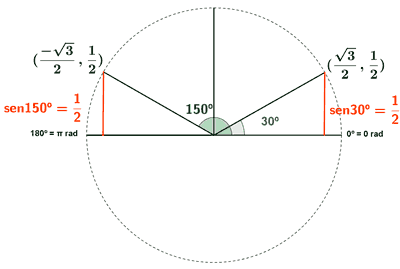
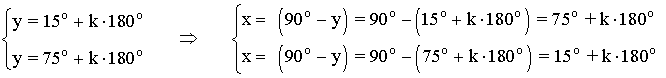
• Por lo tanto las soluciones son las siguientes::

2) Resuelve el siguiente sistema de ecuaciones trigonométricas:
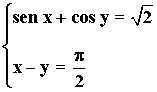
• En primer lugar, calculamos el valor de una de las incógnitas para sustituirlo en la otra ecuación:
x - y = π/2 ⇒ y = π/2 + y
• Sustituyendo en la primera ecuación obtenemos:
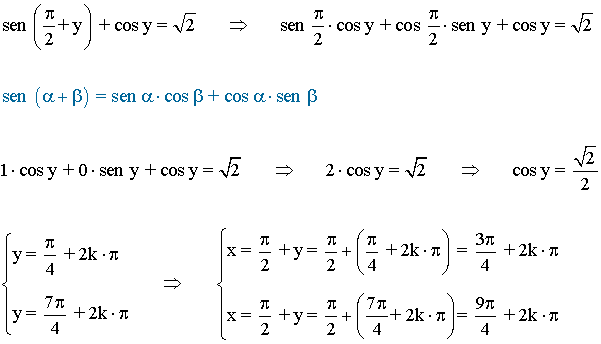
• Por lo tanto las soluciones son las siguientes::
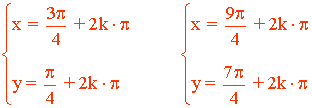
3) Resuelve el siguiente sistema de ecuaciones trigonométricas:
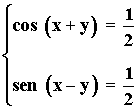
• Las ecuaciones se pueden expresar de la siguiente manera:
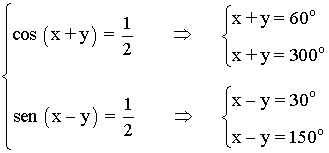
• Por lo tanto el sistema inicial se puede expresar como cuatro sistemas de ecuaciones algebraicas:
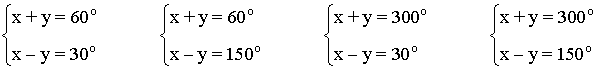
• Las soluciones de dichos sistemas son las siguientes:
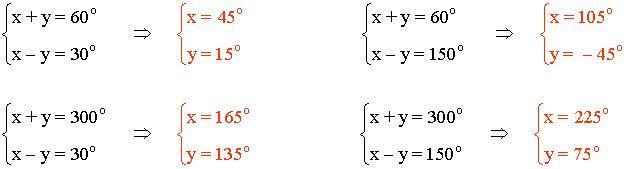
4) Resuelve el siguiente sistema de ecuaciones trigonométricas:
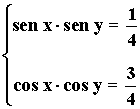
• Sumando ambas ecuaciones obtenemos lo siguiente:
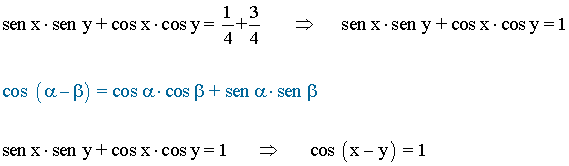
• Restando ambas ecuaciones obtenemos lo siguiente:
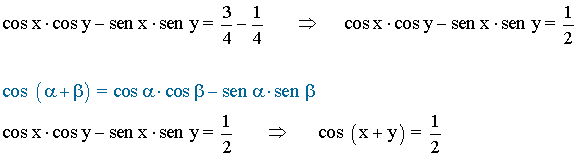
• Ambas condiciones nos dan el siguiente sistema de ecuaciones:
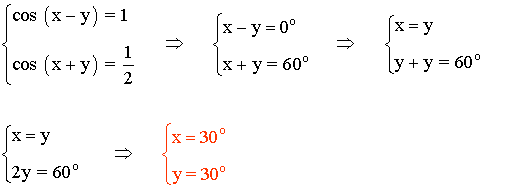
5) Resuelve el siguiente sistema de ecuaciones trigonométricas:
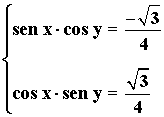
• Sumando ambas ecuaciones obtenemos lo siguiente:
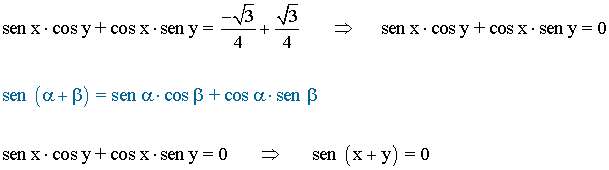
• Restando ambas ecuaciones obtenemos lo siguiente:
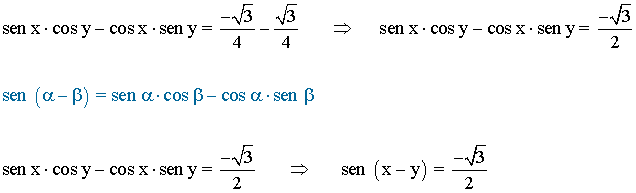
• Ambas condiciones nos dan el siguiente sistema de ecuaciones:
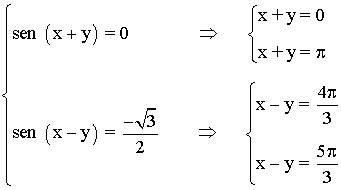
• Obtenemos así cuatro sistemas de ecuaciones:
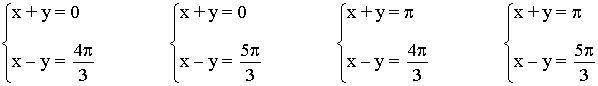
• Las soluciones de cada uno de los sistemas son:
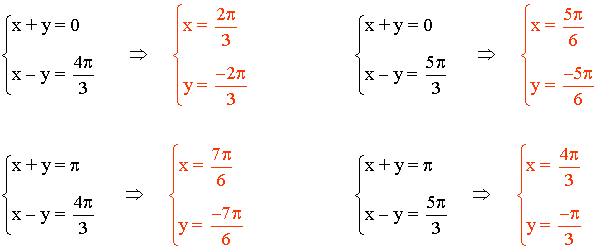
6) Resuelve el siguiente sistema de ecuaciones trigonométricas:
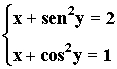
• Sumando ambas ecuaciones obtenemos la siguiente igualdad y aplicamosla fórmula fundamental de la trigonometría:
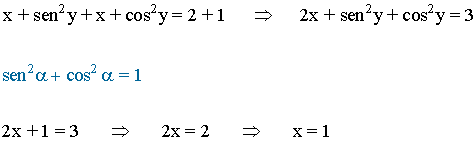
• Sustituimos x = 1 en la primera ecuación:
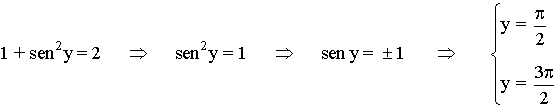
• Las soluciones en el intervalo [0, 2π] son:
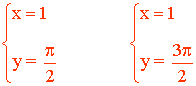
7) Resuelve el siguiente sistema de ecuaciones trigonométricas:
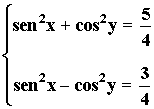
• Sumando ambas ecuaciones obtenemos la siguiente igualdad y aplicamosla fórmula fundamental de la trigonometría:
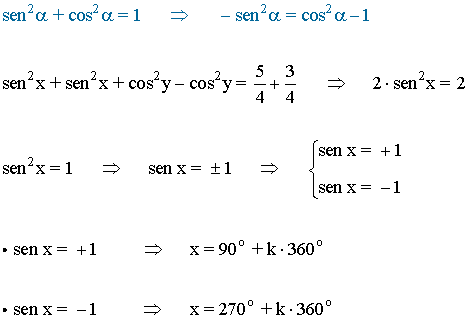
• Sustituimos x = 90o en la primera ecuación:
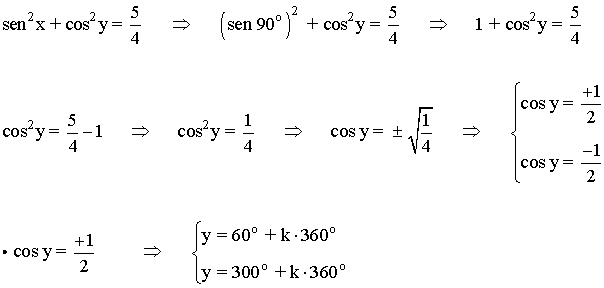
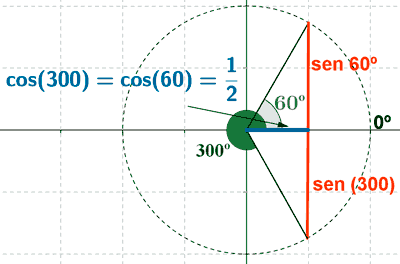
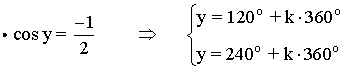
• Sustituimos x = 270o en la primera ecuación:
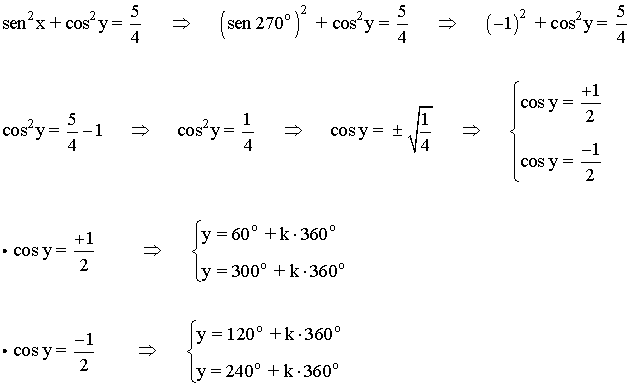
• Las soluciones en el intervalo [0, 2π] son:
| y = 30o | y = 60o | y = 120o | y = 240o | |
|---|---|---|---|---|
| x = 90o | (90o, 30o) |
(90o, 60o) |
(90o, 120o) |
(90o, 240o) |
| x = 270o | (270o, 30o) |
(270o, 60o) |
(270o, 120o) |
(270o, 240o) |
8) Resuelve el siguiente sistema de ecuaciones trigonométricas:
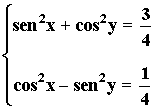
• Sumando ambas ecuaciones obtenemos la siguiente igualdad y aplicamosla fórmula fundamental de la trigonometría:
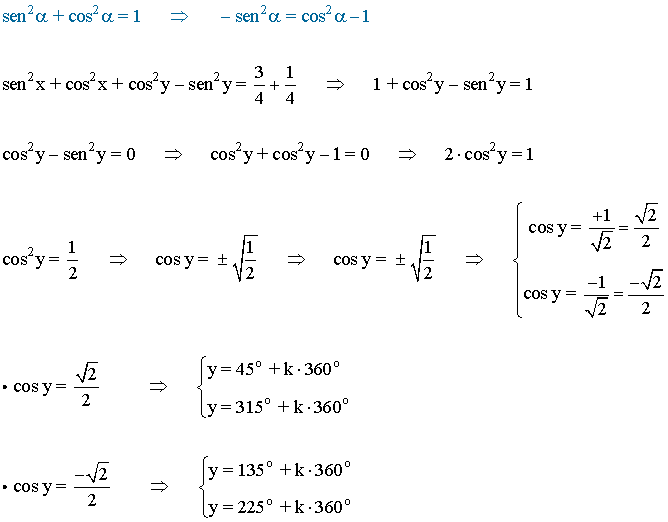
• A continuación sustituimos el valor de y = 45o en la primera ecuación:
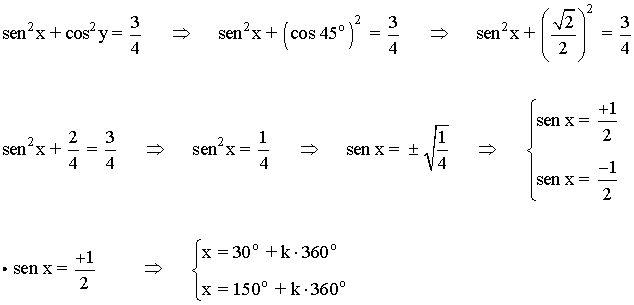

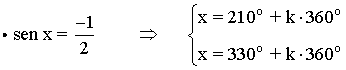
• Las soluciones en el intervalo [0, 2π] son:
| y = 45o | y = 135o | y = 225o | y = 315o | |
|---|---|---|---|---|
| x = 30o | (30o, 45o) |
(30o, 45o) |
(30o, 45o) |
(30o, 45o) |
| x = 45o | (45o, 45o) |
(45o, 45o) |
(45o, 45o) |
(45o, 45o) |
| x = 210o | (210o, 45o) |
(210o, 45o) |
(210o, 45o) |
(210o, 45o) |
| x = 330o | (330o, 45o) |
(330o, 45o) |
(330o, 45o) |
(330o, 45o) |
9) Resuelve el siguiente sistema de ecuaciones trigonométricas:
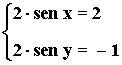
• Los ángulos que verifican cada una de las soluciones son:
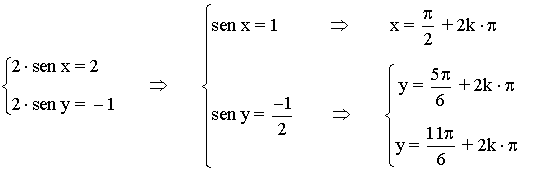
• Por lo tanto, las soluciones son:
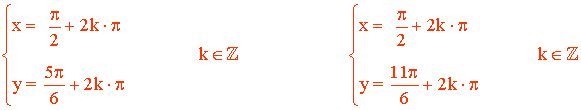
10) Resuelve el siguiente sistema de ecuaciones trigonométricas:
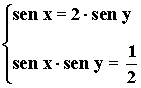
• Realizamos el siguiente cambio de variable:
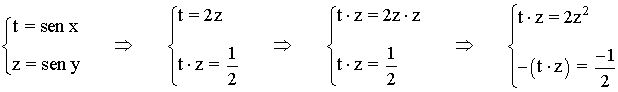
• Sumando ambas ecuaciones obtenemos:
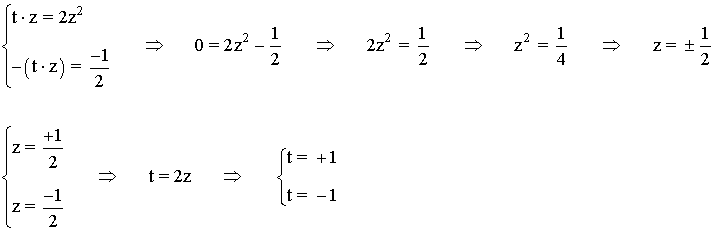
• Deshaciendo los cambios de variable tenemos que:
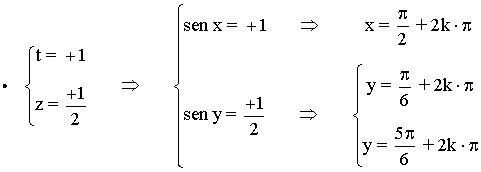

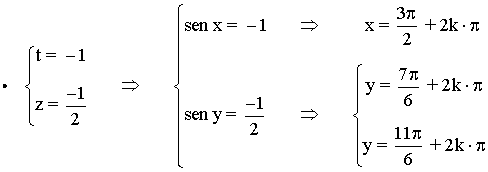
• Por tanto las soluciones son:
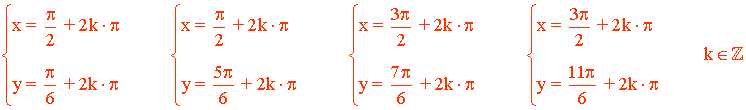
11) Resuelve el siguiente sistema de ecuaciones trigonométricas:
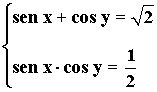
• Despejamos cos y de la primera ecuación:
![]()
• Sustituimos el valor obtenido en la segunda ecuación y desarrollamos:
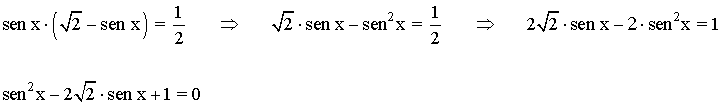
• Resolvemos la ecuación de segundo grado:
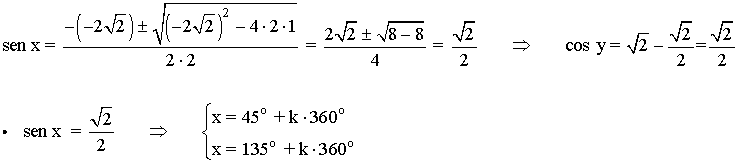
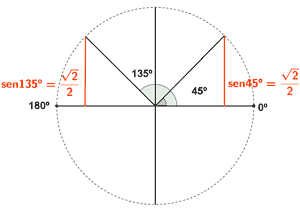
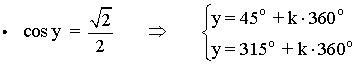
• Por tanto las soluciones son:
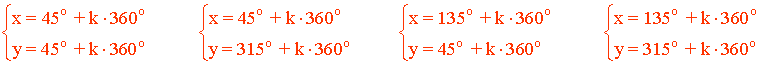
12) Resuelve el siguiente sistema de ecuaciones trigonométricas:
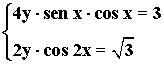
• Dividimos las dos ecuaciones del sistema:
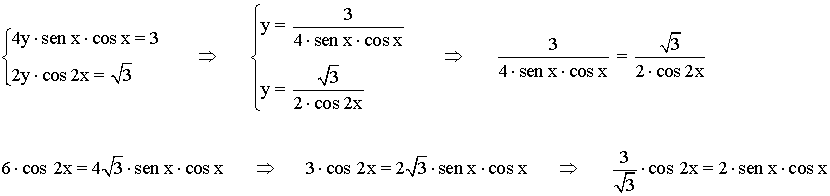
• Aplicamos la fórmula del ángulo doble:
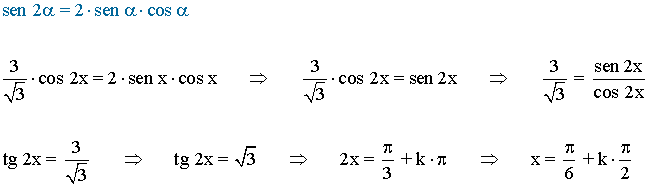
La función tangente tiene periodo 180o o π radianes , por lo tanto encontramos las soluciones en el intervalo (-π/2, π/2) y luego sumamos multiplos de π .
• Despejamos el valor de y de la segunda ecuación:
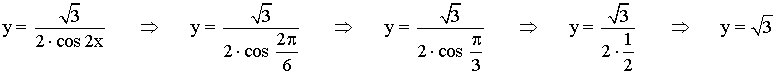
• Por tanto las soluciones son:
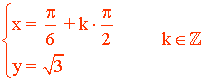
13) Resuelve el siguiente sistema de ecuaciones trigonométricas:
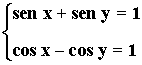
• Despejamos de ambas ecuaciones sen x y cos x :
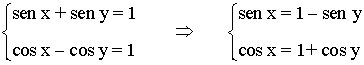
• Elevamos ambas ecuaciones al cuadrado:
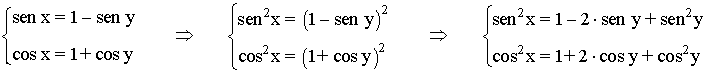
• A continuación, sumando ambas ecuaciones obtenemos:
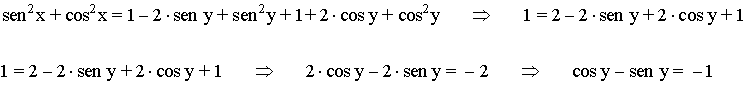
• Aplicamos la siguiente igualdad:
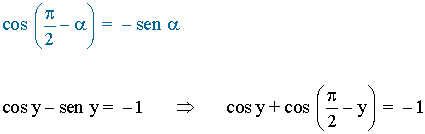
• Desarrollamos la expresión para transformar la suma en producto:
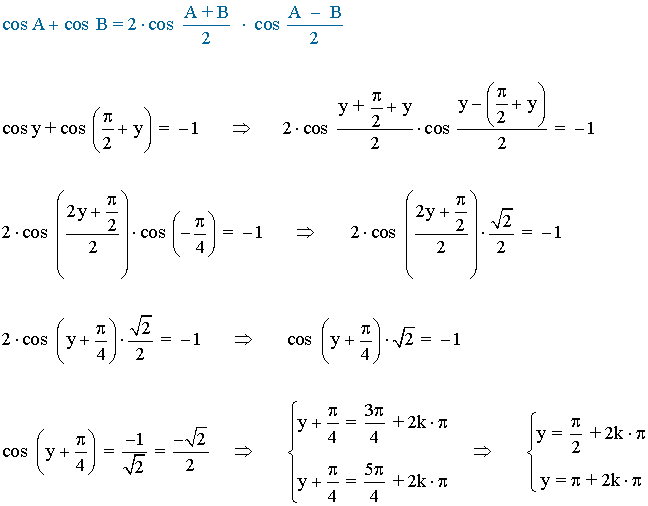
• Despejamos el valor de x para cada solución de y :
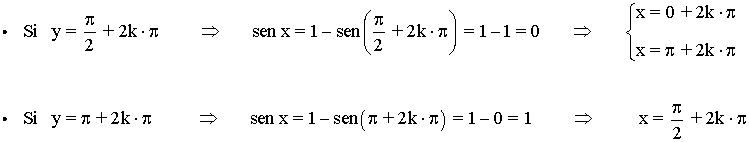
• Los pares de soluciones son los siguientes:
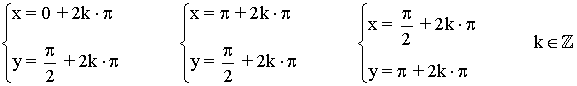
• Al elevar al cuadrado las ecuaciones, algunas de las soluciones pueden ser no validas, por lo que comprobamos cada una de ellas:
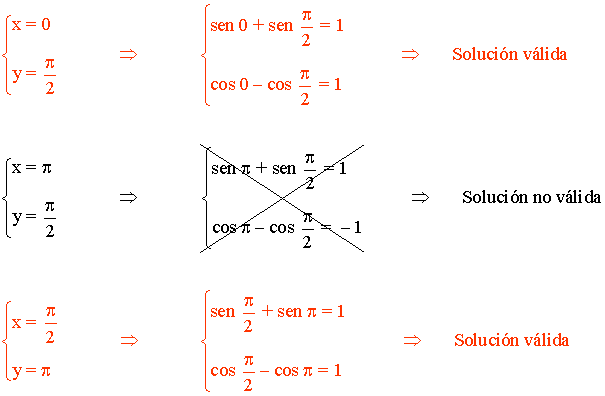


 INICIO
INICIO