Ejercicios resueltos de ecuaciones trigonométricas
1) Resuelve las siguientes ecuaciones trigonométricas en ángulos y radianes:
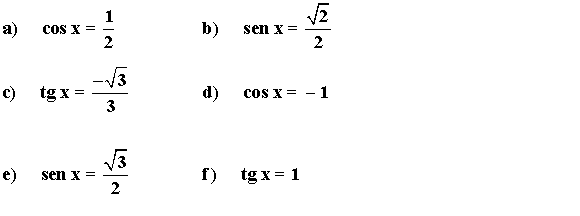
2) Resuelve las siguientes ecuaciones trigonométricas:
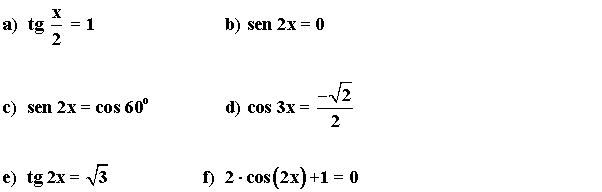
3) Resuelve las siguientes ecuaciones trigonométricas:
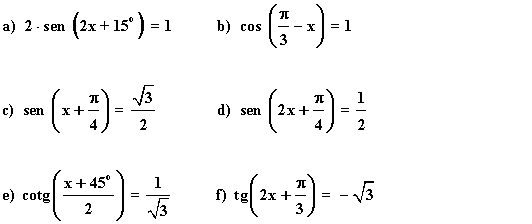
4) Resuelve las siguientes ecuaciones trigonométricas:
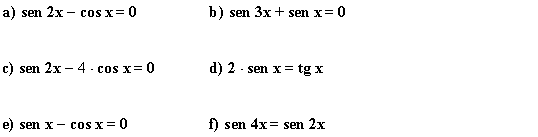
5) Resuelve las siguientes ecuaciones trigonométricas:
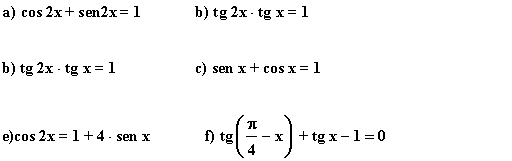
6) Resuelve las siguientes ecuaciones trigonométricas y expresa la solución en radianes:
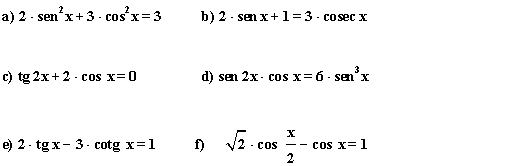
7) Resuelve las siguientes ecuaciones trigonométricas:
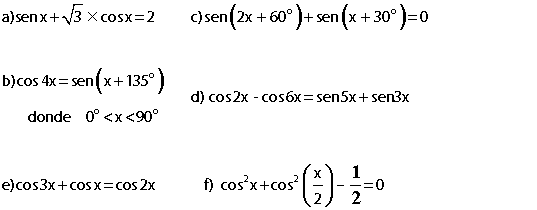
8) Resuelve las siguientes ecuaciones trigonométricas:
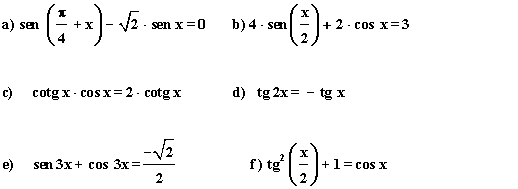
1) Resuelve las siguientes ecuaciones trigonométricas en ángulos y radianes:
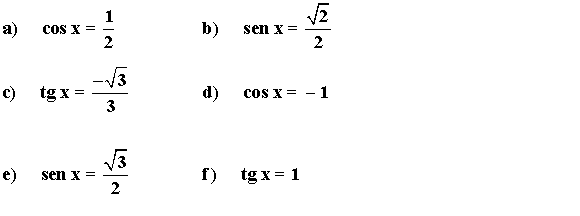
(a)
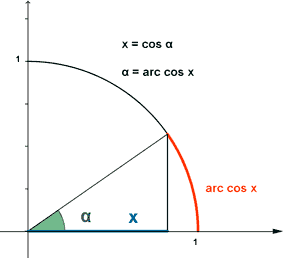
Para resolver la ecuación cos x = 1/2 hay que buscar los ángulos cuyo coseno valga 1/2
Lo expresamos como x = arc cos 1/2 que expresa que x es el ángulo cuyo coseno es 1/2
Como el coseno es positivo en el primer y cuarto cuadrante, tendrá dos soluciones en el primer giro.
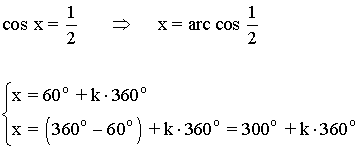
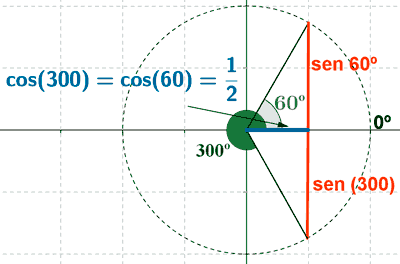
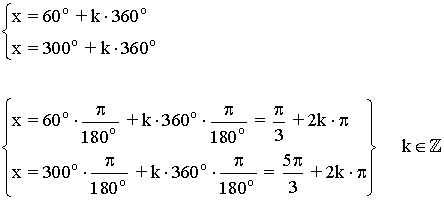
Soluciones del primer giro son 60o y 300o
Los demás ángulos que cumplen la ecuación son los que se obtienen al sumar o restar vueltas completas a las dos soluciones halladas, es decir: 60o + k·360o y 300o + k·360o
(b)
Para resolver la ecuación hay que buscar los ángulos tal que:

Que expresa que x es el ángulo cuyo coseno es (√2)/2
Como el coseno es positivo en el primer y segundo cuadrante, tendrá dos soluciones en el primer giro
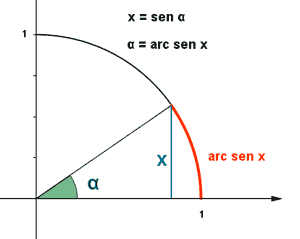
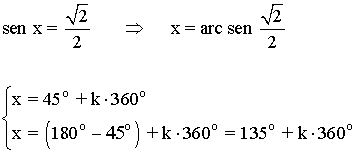
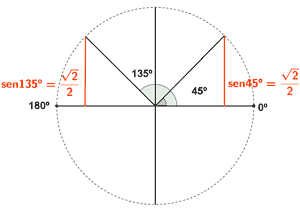
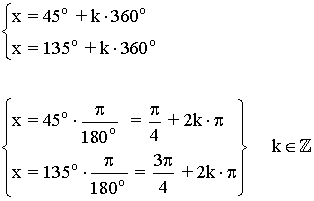
Soluciones del primer giro son 45o y 135o
Los demás ángulos que cumplen la ecuación son los que se obtienen al sumar o restar vueltas completas a las dos soluciones halladas, es decir: 45o + k·360o y 135o + k·360o
(c)
Para resolver la ecuación hay que buscar los ángulos tal que:

Que expresa que x es el ángulo cuya tangente es (√3)/3
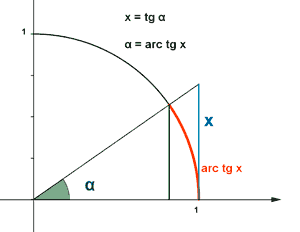
Como la tangente es negativa en el segundo y cuarto cuadrante, tendrá dos soluciones en el primer giro.
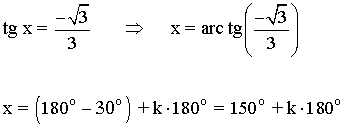
![]()
La función tangente tiene periodo 180o o π radianes , por lo tanto encontramos las soluciones en el intervalo (-π/2, π/2) y luego sumamos multiplos de π .
Las soluciones en el intervalo [0, 2π] son: 150o y 330o
Los demás ángulos que cumplen la ecuación son los que se obtienen al sumar o restar π a las dos soluciones halladas, es decir: 150o + k·180o y 330o + k·180o
(d)
Para resolver la ecuación hay que buscar los ángulos tal que:
![]()
Que expresa que x es el ángulo cuyo coseno es - 1
Como el coseno solo toma el valor - 1 en el eje negativo de coordenadas, solo tendrá una solución en el primer giro.
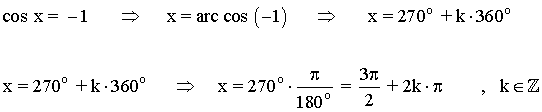
Solución del primer giro es 270o
Los demás ángulos que cumplen la ecuación son los que se obtienen al sumar o restar vueltas completas a las dos soluciones halladas, es decir: 270o + k·360o
(e)
Para resolver la ecuación hay que buscar los ángulos tal que:
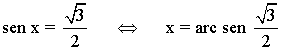
Como el seno toma valores positivos en el primer y segundo cuadrante, tendrá dos soluciones en el primer giro.
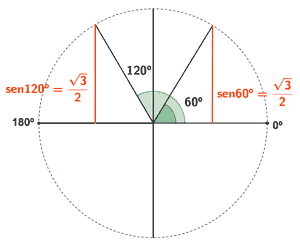
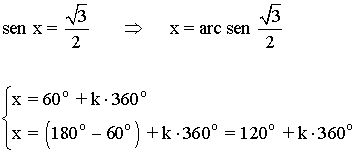
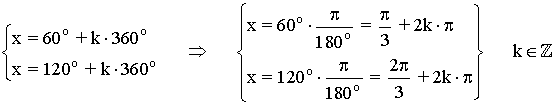
Soluciones del primer giro son 60o , 120o
Los demás ángulos que cumplen la ecuación son los que se obtienen al sumar o restar vueltas completas a las dos soluciones halladas, es decir: x = 60o + k·360o , x = 120o + k·360o
(f)
Para resolver la ecuación hay que buscar los ángulos tal que:
![]()
Como la tangente toma valores positivos en el primer y tercer cuadrante, tendrá dos soluciones en el primer giro.
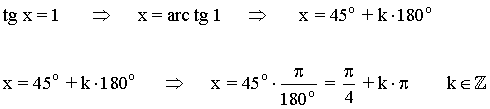
La función tangente tiene periodo 180o o π radianes , por lo tanto encontramos las soluciones en el intervalo (-π/2, π/2) y luego sumamos multiplos de π .
Las soluciones en el intervalo [0, 2π] son: π/4 = 45o , 5π/4 = 225o
Los demás ángulos que cumplen la ecuación son los que se obtienen al sumar o restar π a las dos soluciones halladas, es decir: x = π/4 + k·π , x = 5π/4 + k·π
2) Resuelve las siguientes ecuaciones trigonométricas:
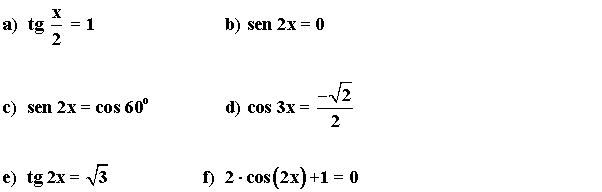
(a)
Para resolver la ecuación tg x/2 = 1 hay que buscar los ángulos cuya tangente valga 1 .
Lo expresamos como x/2 = arc tg 1 que expresa que x/2 es el ángulo cuya tangente es 1 .
Como la tangente es positiva en el primer y tercer cuadrante, buscamos las dos soluciones.
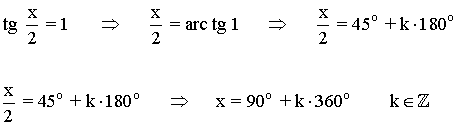
La función tangente tiene periodo 180o o π radianes , por lo tanto encontramos las soluciones en el intervalo (-π/2, π/2) y luego sumamos multiplos de π .
La solucióon en el intervalo [0, 2π] es: x = 90o
Los demás ángulos que cumplen la ecuación son los que se obtienen al sumar o restar 2π a las dos soluciones halladas, es decir: 90o + 2k·π
(b)
Para resolver la ecuación sen 2x = 0 hay que buscar los ángulos cuya tangente valga 0
Lo expresamos como 2x = arc sen 0 que expresa que 2x es el ángulo cuyo seno es 0
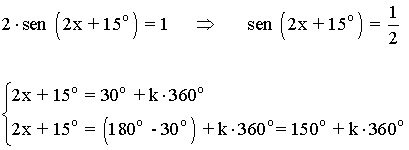
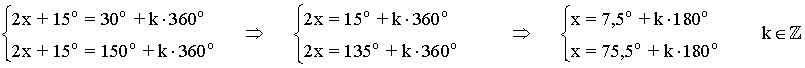
(c)
Para resolver la ecuación sen 2x = cos 60o sustituimos el valor de cos 60o
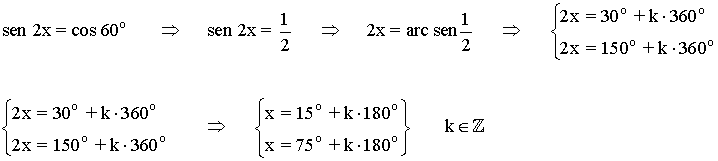
(d)
El coseno toma valores negativos en el segundo y tercer cuadrante:
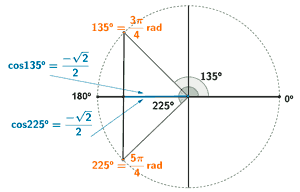
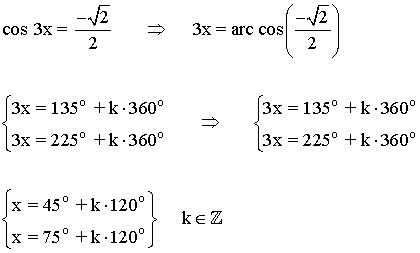
(e)
La tangente toma valores positivos en el primer y tercer cuadrante:
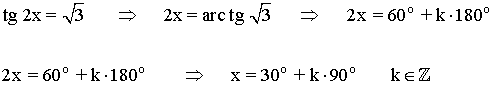
La función tangente tiene periodo 180o o π radianes , por lo tanto encontramos las soluciones en el intervalo (-π/2, π/2) y luego sumamos multiplos de π .
Las soluciones en el intervalo [0, 2π] son:
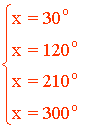
(f)
Resolvemos la ecuación para encontrar los ángulos que cumplen la igualdad:
![]()
El coseno toma valores negativos en el segundo y tercer cuadrante:
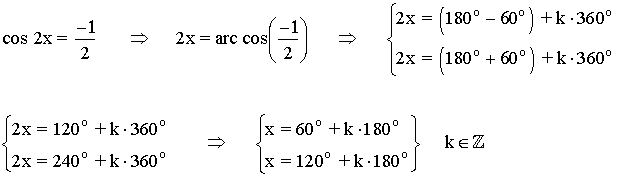
3) Resuelve las siguientes ecuaciones trigonométricas:
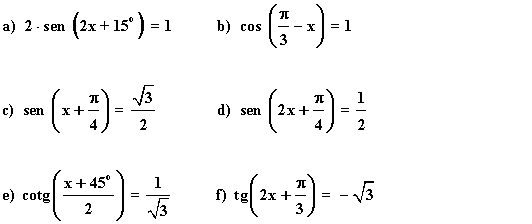
(a)
Para resolver la ecuación hay que buscar los ángulos cuyo seno valga 1/2
Como el seno es positivo en el primer y segundo cuadrante, buscamos las dos soluciones
Los del primer giro son 30o y 150o pero encontraremos más en las siguientes vueltas

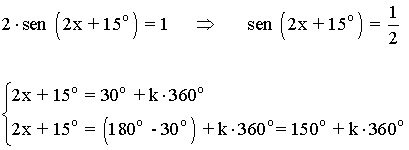
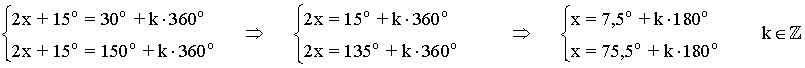
Las soluciones del primer giro para k = 0 son 7,5o y 67,5o
Las soluciones del primer giro para k = 1 son 187,5o y 247,5o
(b)
Sabemos que el coseno toma el valor 1 en el ángulo 0 radianes:
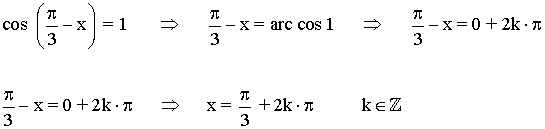
(c)
Sabemos que el seno toma valores positivos en el primer y segundo cuadrante:
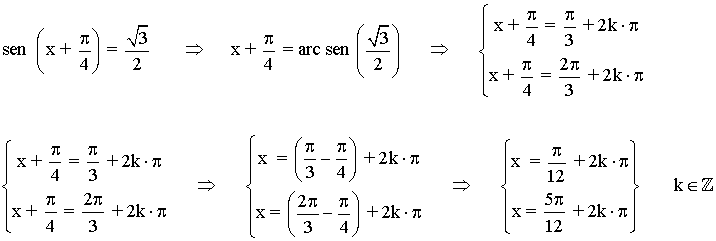
(d)
Sabemos que el seno toma valores positivos en el primer y segundo cuadrante:
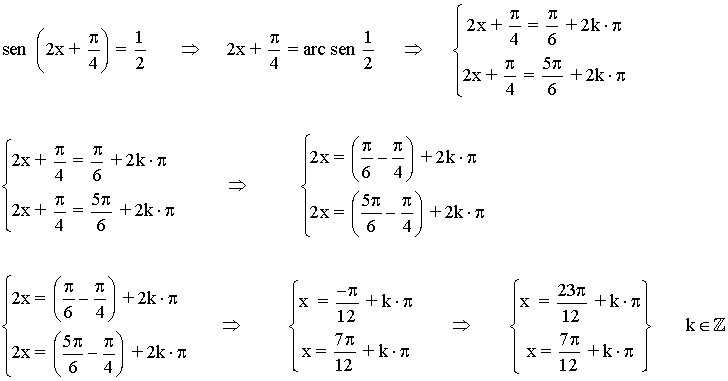
(e)
Antes de buscar la solución a la ecuación, despejamos la cotangente:
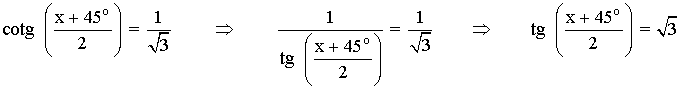
La tangente es positiva en el primer y tercer cuadrante:
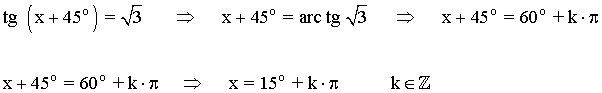
La función tangente tiene periodo 180o o π radianes , por lo tanto encontramos las soluciones en el intervalo (-π/2, π/2) y luego sumamos multiplos de π .
Las soluciones en el intervalo [0, 2π] son: π/12 = 15o , 13π/12 = 225o
Los demás ángulos que cumplen la ecuación son los que se obtienen al sumar o restar π a las dos soluciones halladas, es decir: x = π/12 + k·π
(f)
La tangente es negativa en el segundo y tercer cuadrante:
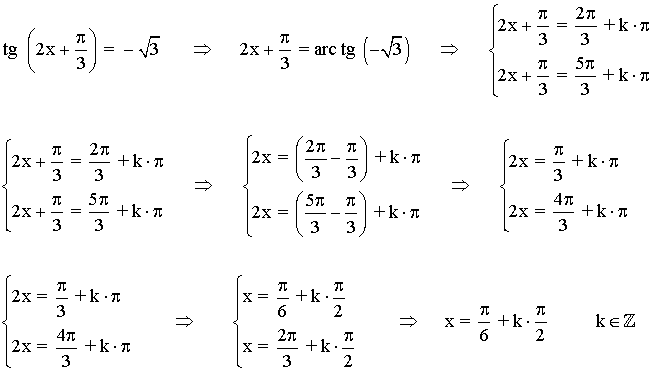
4) Resuelve las siguientes ecuaciones trigonométricas:
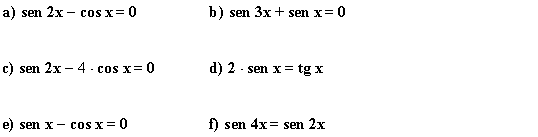
(a)
Para resolver la ecuación hay que factorizar y resolver cada una de las ecuaciones
El coseno se anula en el primer giro en 90o y 270o
El seno es positivo en el primer y segundo cuadrante
Los del primer giro son 30o y 150o pero encontraremos más en las siguientes vueltas
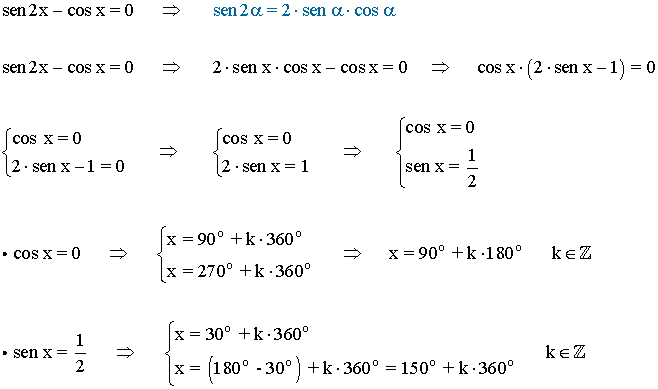
Las soluciones del primer giro son 30o , 90o , 150o , 270o
(b)
Para resolver la ecuación hay que factorizar y resolver cada una de las ecuaciones
El seno se anula en 0o y 180o pero encontraremos más en las siguientes vueltas
El coseno se anula en el primer giro en 90o y 270o
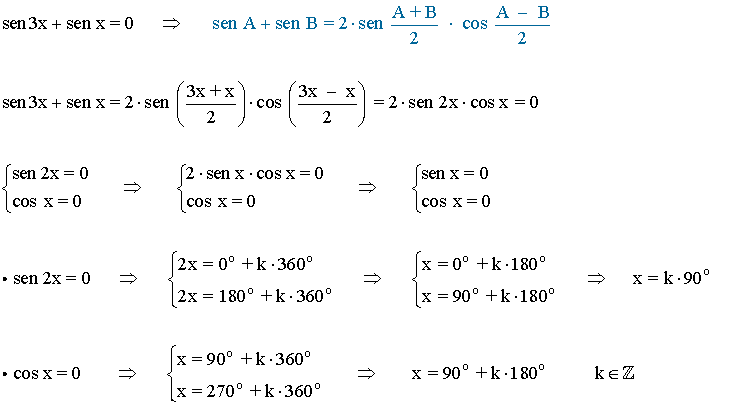
Las soluciones del primer giro son 0o , 90o , 180o , 270o
(c)
Para resolver la ecuación hay que factorizar y resolver cada una de las ecuaciones
Recordamos que el coseno se anula en el primer giro en 90o y 270o
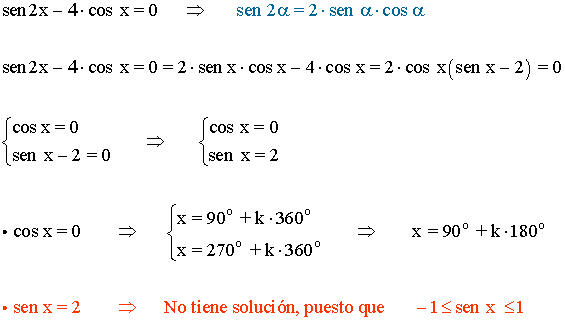
(d)
Para resolver la ecuación hay que factorizar y resolver cada una de las ecuaciones
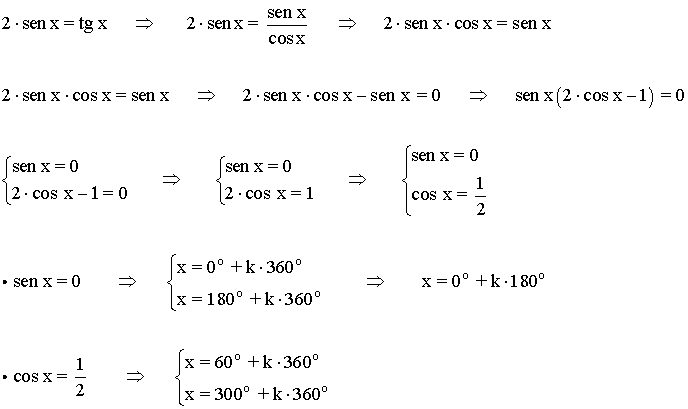
(e)
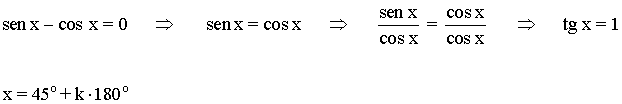
La función tangente tiene periodo 180o o π radianes , por lo tanto encontramos las soluciones en el intervalo (-π/2, π/2) y luego sumamos multiplos de π .
(f)
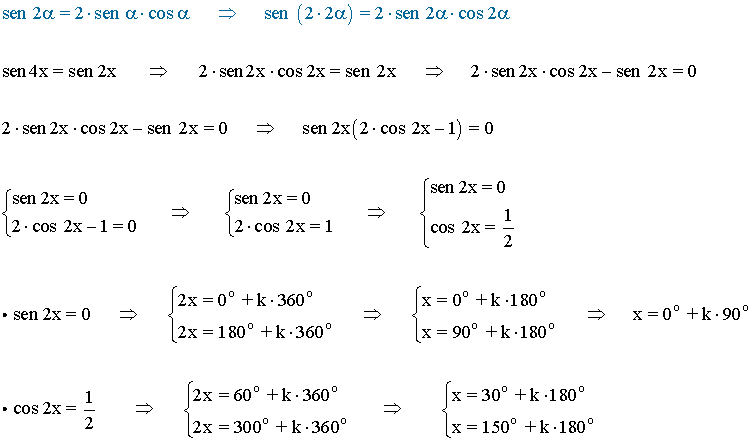
5) Resuelve las siguientes ecuaciones trigonométricas:
(a)
Para resolver la ecuación se desarrolla cos 2x y resulta una ecuación de segundo grado incompleta:
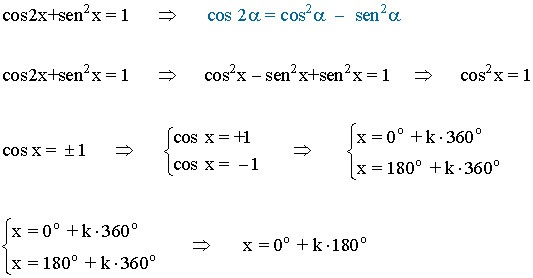
(b)
Para resolver la ecuación se desarrolla tg 2x y resulta una ecuación de segundo grado incompleta:
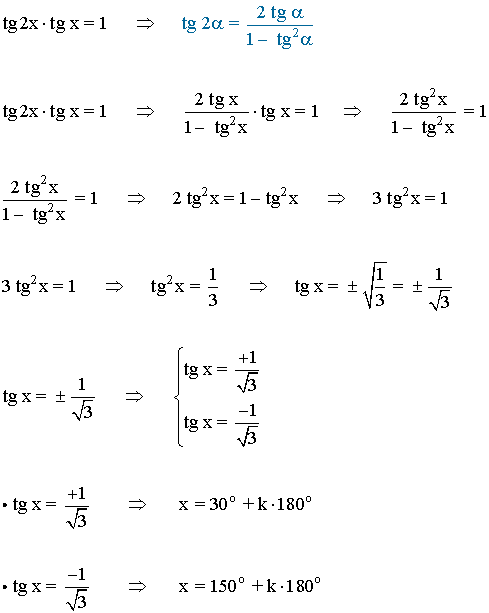
La función tangente tiene periodo 180o o π radianes , por lo tanto encontramos las soluciones en el intervalo (-π/2, π/2) y luego sumamos multiplos de π .
Las soluciones en el intervalo [0, 2π] son: π/6 = 30o , 5π/6 = 150o , 7π/6 = 210o , 11π/6 = 330o
(c)
Para resolver la ecuación elevamos ambos miembros al cuadrado. Hay que tener en cuenta que en nuestro caso, al resolver la ecuación elevando ambos términos al cuadrado, también vamos a obtener las soluciones de senx + cos x = -1
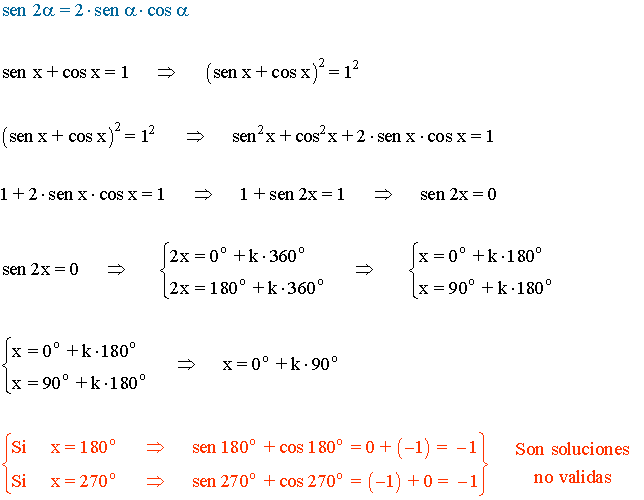
(d)
Para resolver la ecuación se aplica la fórmula fundamental de la trigonometría y resulta una ecuación de segundo grado incompleta:
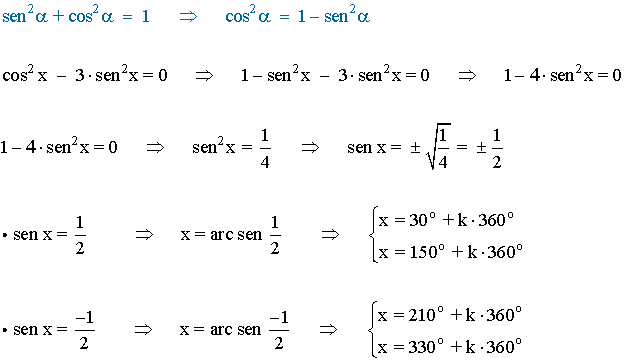
(e)
Para resolver la ecuación se desarrolla cos 2x y resulta una ecuación de segundo grado incompleta:

(f)
Para resolver la ecuación se desarrolla la fórmula de la diferencia de ángulos de la tangente y resulta una ecuación de segundo grado incompleta:
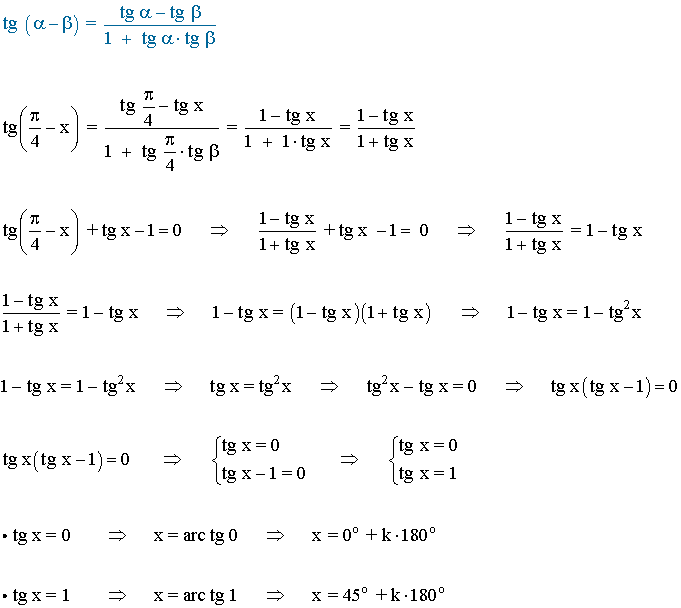
La función tangente tiene periodo 180o o π radianes , por lo tanto encontramos las soluciones en el intervalo (-π/2, π/2) y luego sumamos multiplos de π .
6) Resuelve las siguientes ecuaciones trigonométricas y expresa la solución en radianes:
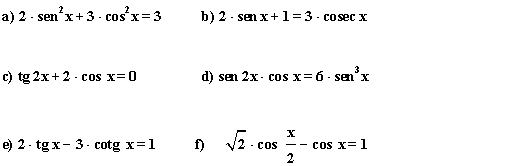
(a)
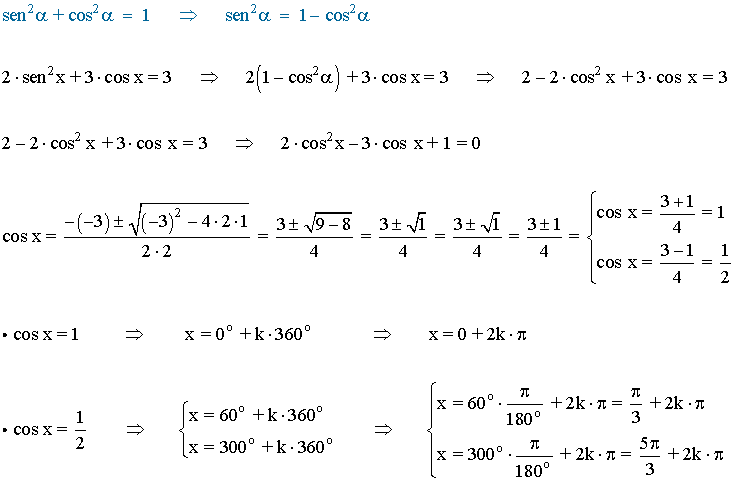
(b)
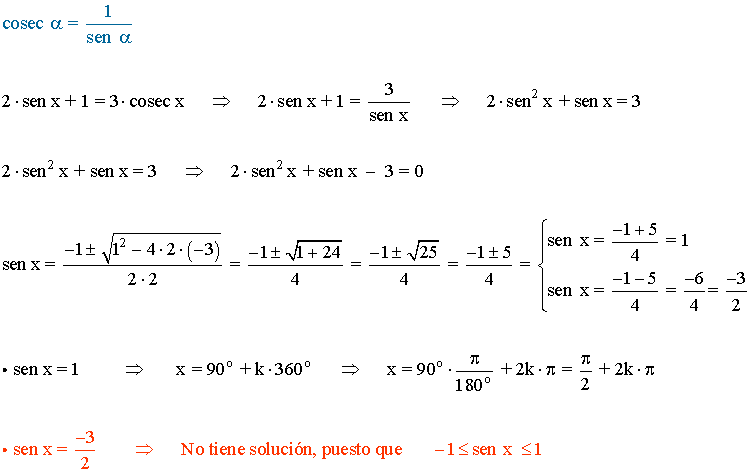
(c)
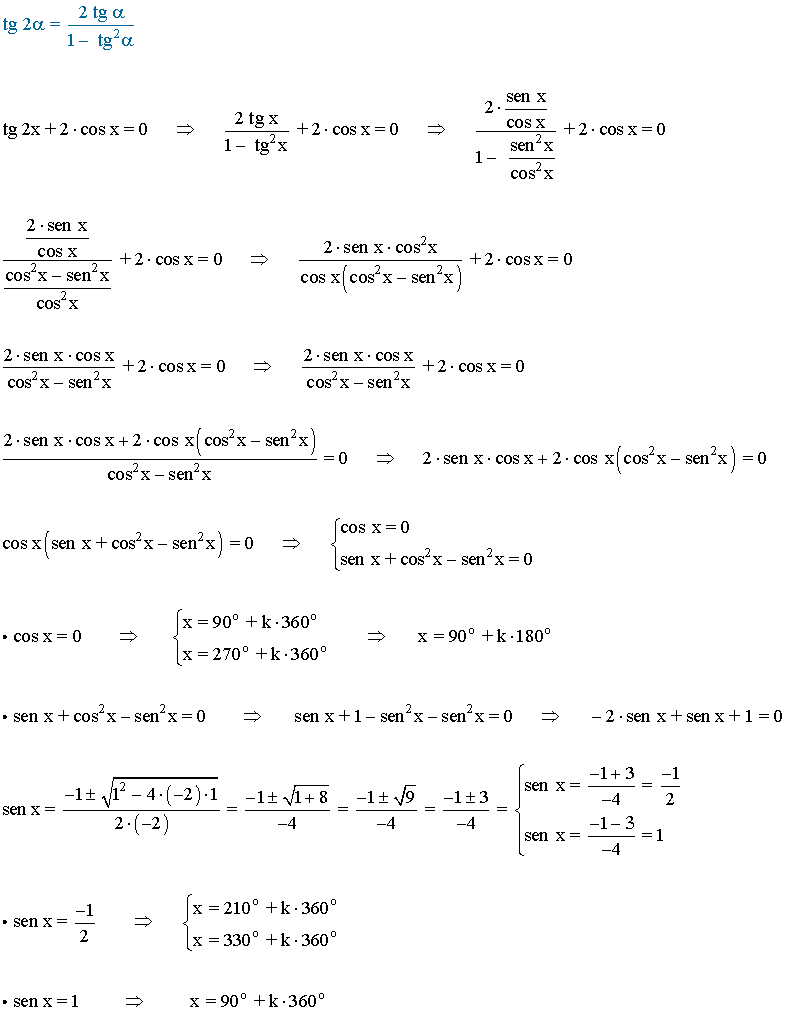
Recopilamos las soluciones y las expresamos en forma de radianes:
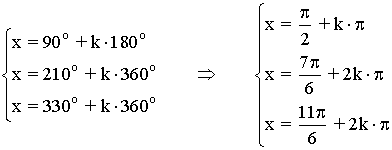
(d)

Recopilamos las soluciones y las expresamos en forma de radianes:
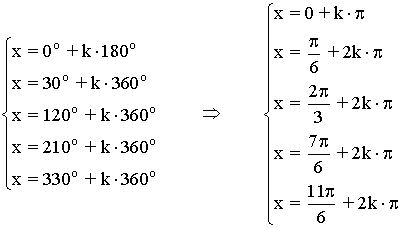
(e)
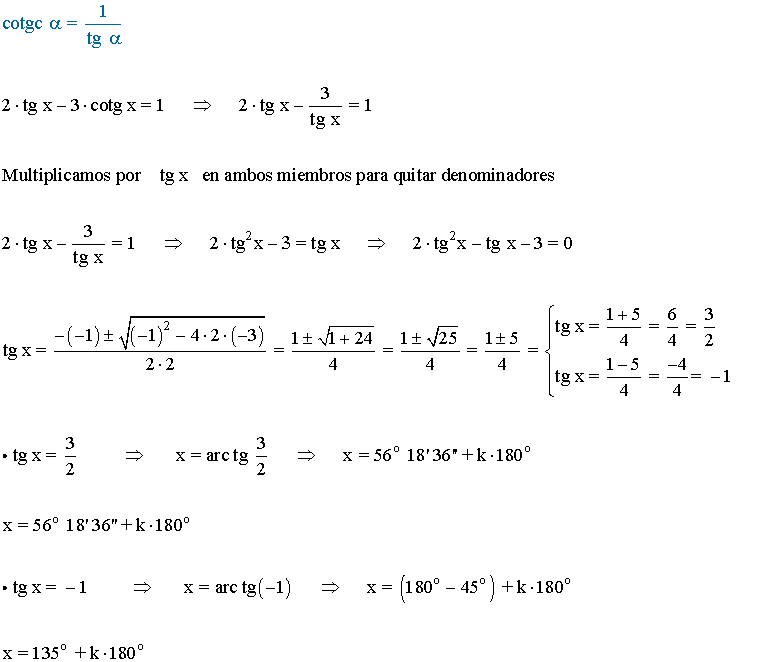
La función tangente tiene periodo 180o o π radianes , por lo tanto encontramos las soluciones en el intervalo (-π/2, π/2) y luego sumamos multiplos de π .
Recopilamos las soluciones y las expresamos en forma de radianes:
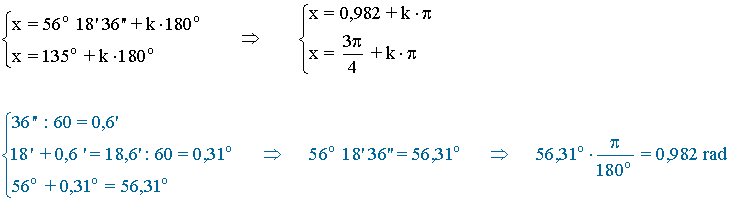
(f)

Recopilamos las soluciones y las expresamos en forma de radianes:
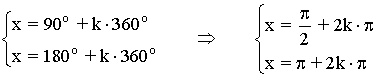
7) Resuelve las siguientes ecuaciones trigonométricas:
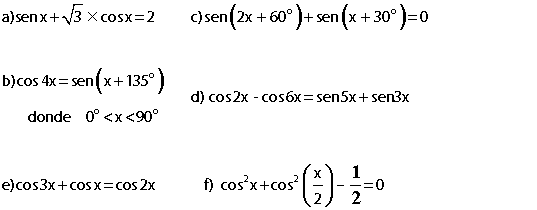
(a)
Para resolver la ecuación aplicamos la fórmula de la adición de ángulos:
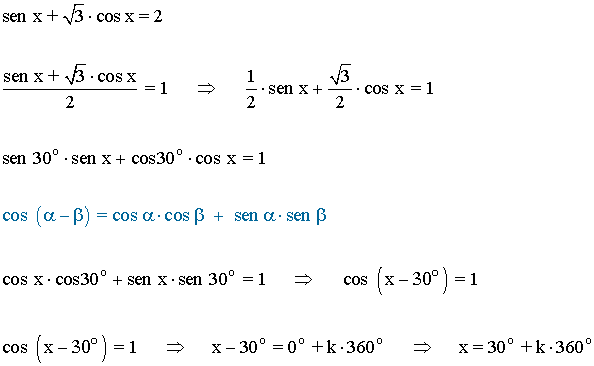
(b)
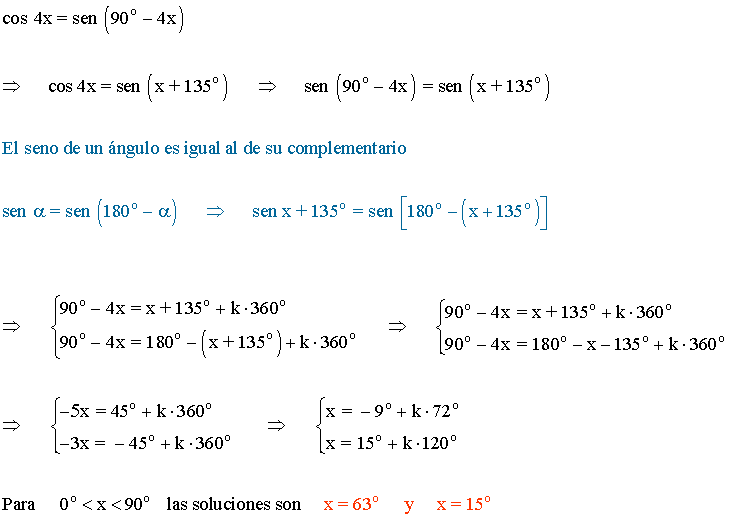
(c)
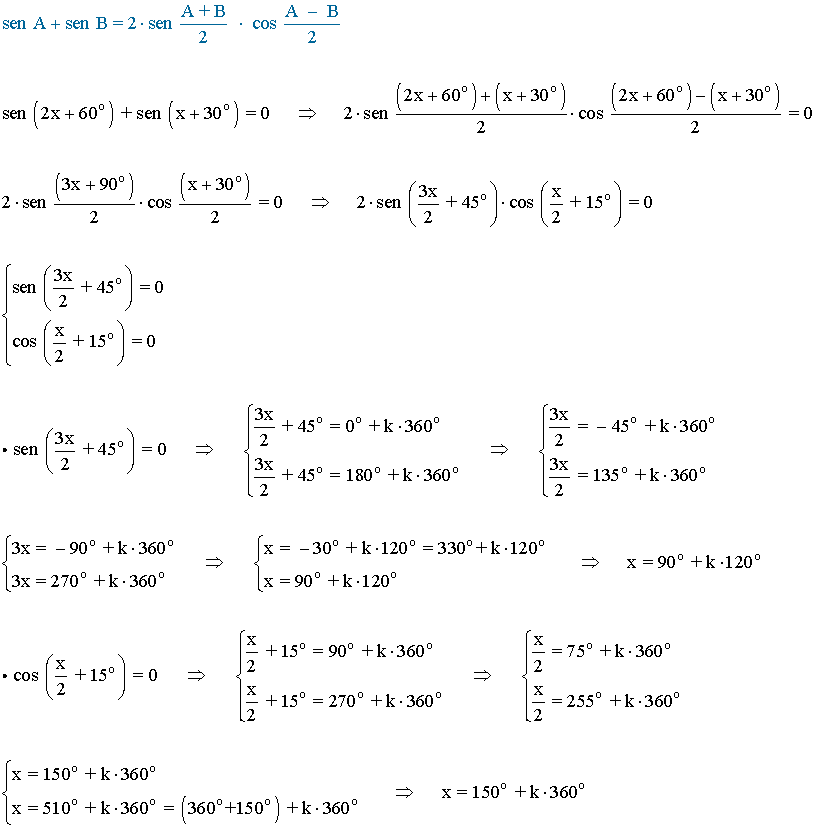
Agrupamos las soluciones:
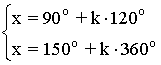
(d)

Agrupamos las soluciones:
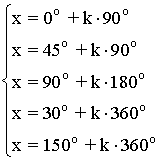
(e)
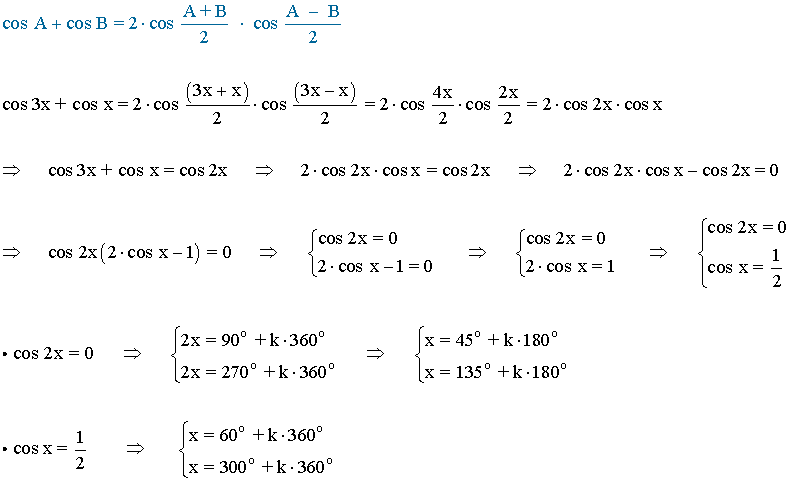
Agrupamos las soluciones:
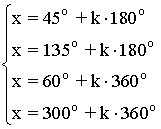
También podemos resolver la ecuación de otra manera. Para ello desarrollamos cos 3x
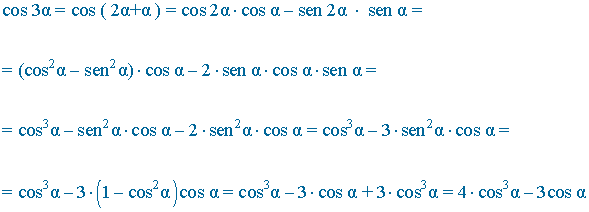
Por otra parte desarrollamos cos 2x
![]()
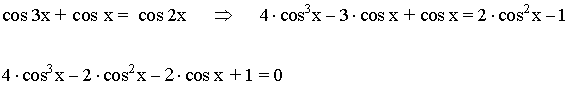
Realizamos el siguiente cambio de variable: t = cos x
Por lo tanto, la ecuación anterior quedaría de la siguiente forma:
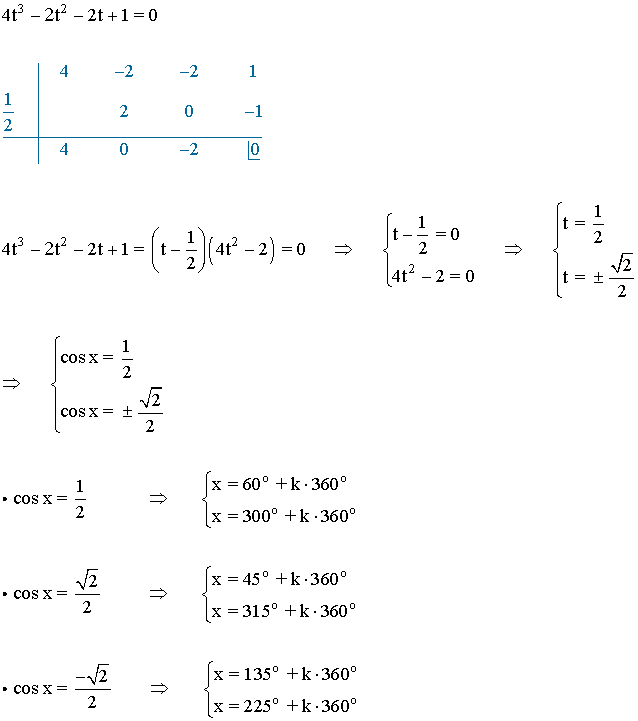
(f)
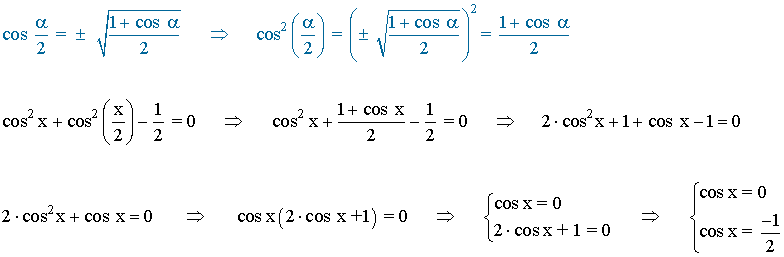
La función coseno tiene periodo 360o o 2π radianes , por lo tanto encontramos las soluciones en el intervalo [0, 2π] y luego sumamos multiplos de 2π .
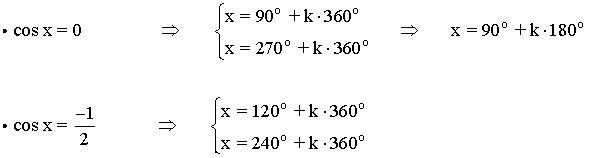
Agrupamos las soluciones:
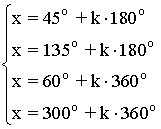
8) Resuelve las siguientes ecuaciones trigonométricas:
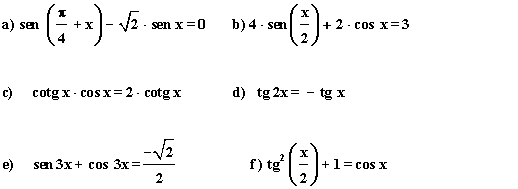
(a)
Aplicamos la fórmula de la suma de ángulos:
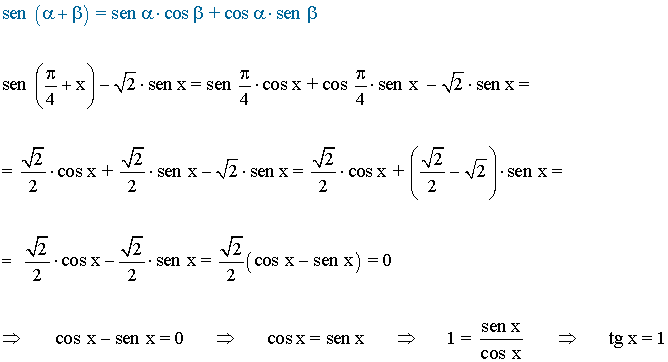
La función tangente tiene periodo 180o o π radianes , por lo tanto encontramos las soluciones en el intervalo (-π/2, π/2) y luego sumamos multiplos de π .
![]()
Las soluciones en el intervalo [0, 2π] son:
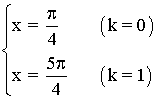
(b)
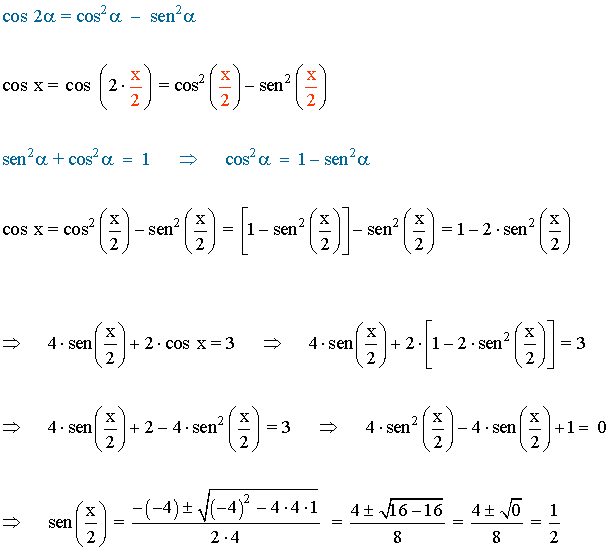
La función seno tiene periodo 360o o 2π radianes , por lo tanto encontramos las soluciones en el intervalo [0, 2π] y luego sumamos multiplos de 2π .
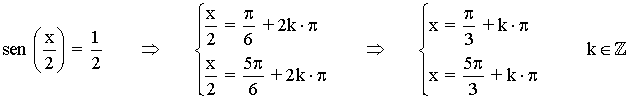
(c)
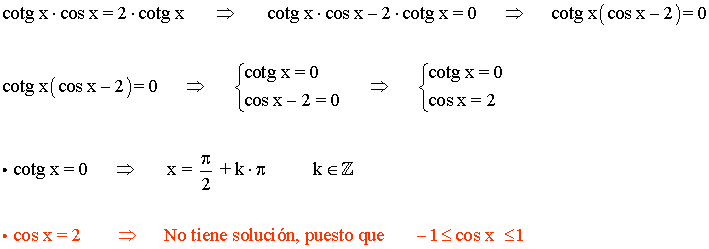
La función cotangente tiene periodo π radianes , por lo tanto encontramos las soluciones en el intervalo (0, π) y luego sumamos multiplos de π .
(d)

La función tangente tiene periodo π radianes , por lo tanto encontramos las soluciones en el intervalo (-π/2, π/2) y luego sumamos multiplos de π .
(e)
En primer lugar convertimos el coseno en seno utilizando para ello los ángulos complementarios. De esta forma podemos utilizar despues la fórmula de la suma de senos:
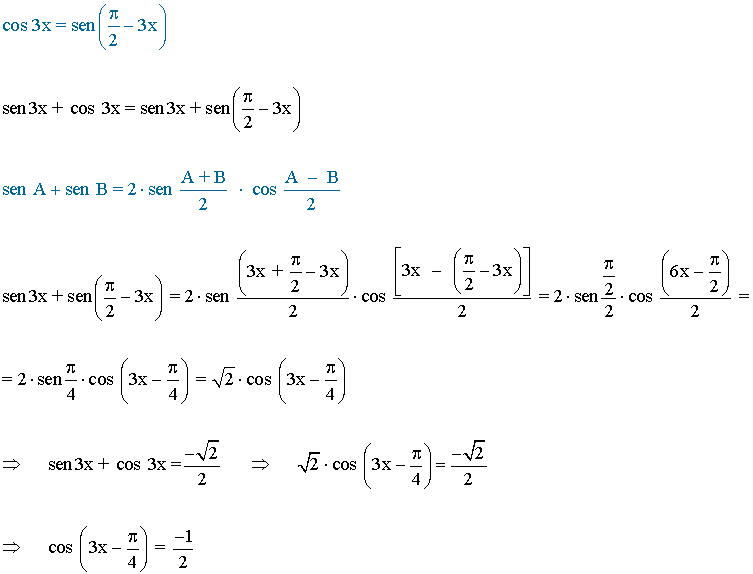
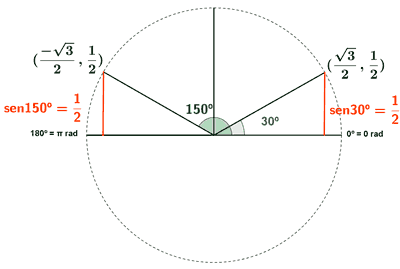
La función coseno toma valores negativos en el segundo y tercer cuadrante, por tanto los valores son:
2π/3 = 120o y 4π/3 = 240o
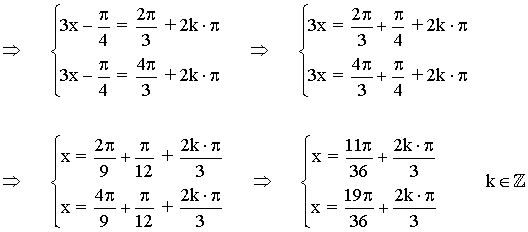
La función coseno tiene periodo 2π radianes , por lo tanto encontramos las soluciones en el intervalo (0, 2π) y luego sumamos multiplos de 2π .
(f)
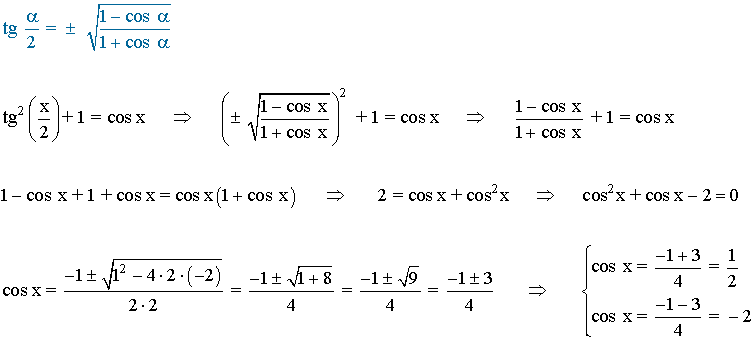
La función coseno toma valores positivos en el segundo y tercer cuadrante, por tanto los valores son:
π/3 = 120o y 5π/3 = 240o
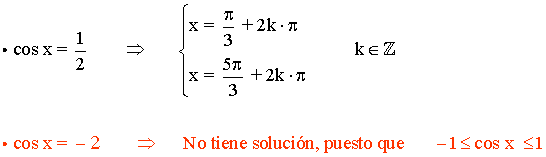
La función coseno tiene periodo 2π radianes , por lo tanto encontramos las soluciones en el intervalo (0, 2π) y luego sumamos multiplos de 2π .


 INICIO
INICIO