Rectas paralelas y perpendiculares
Rectas paralelas
Para que dos rectas sean paralelas, el ángulo que forman entre ellas es de 0º:
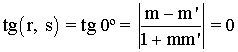
es decir, el numerador tiene que ser igual a 0, por lo tanto:
![]()
Ejemplo:
Determina el valor de t para que las siguientes rectas sean paralelas:
r: 3x - 4y + 12 = 0
s: tx + 8y - 15 = 0
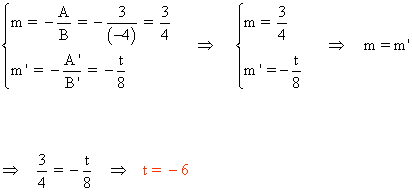
Rectas perpendiculares
Para que dos rectas sean perpendiculares, el ángulo que forman entre ellas es de 90º:
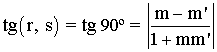
es decir, el denominador tiene que ser igual a 0, por lo tanto:
![]()
Si dos rectas son perpendiculares, la pendiente de una es la inversa de la otra cambiada de signo.
Ejemplo:
1) Determina el valor de t para que las siguientes rectas sean perpendiculares:
r: 3x - 4y + 12 = 0
s: tx + 8y - 15 = 0
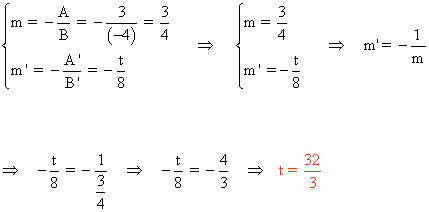
2) Halla la ecuación general de la recta paralela a 3x - 2y + 5 = 0 y pasa por el punto A(-2, 1) .
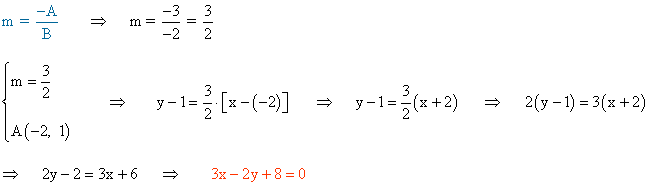
También podemos hallarla de la siguiente manera:
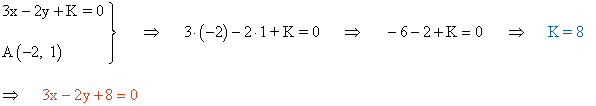
3) Halla la ecuación general de la recta perpendicular a 2x + y - 3 = 0 que pasa por el punto A ( 1 , 1 ).
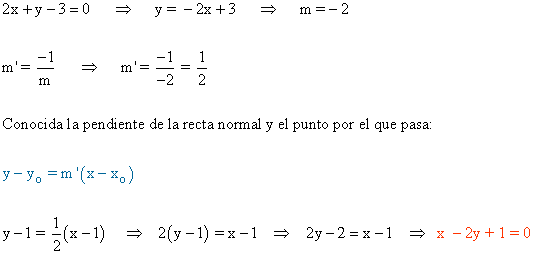
También podemos calcular la ecuación utilizando el vector normal a la recta:



 INICIO
INICIO

