Problemas resueltos de áreas I
1) Calcular el área del recinto limitado por la gráfica de la función f(x) = x2 - 4 , el eje OX y la recta x = 3 .
2) Calcular el área encerrada por la curva: y = x2 - 4x
y la recta: y = 2x - 5
3) Determinar el área encerrada entre las gráficas de las funciones de ecuaciones:
y = 6x - x2 , y = x2 - 2x
4) Se consideran, en el plano, las curvas de ecuaciones:

Dibujar estas curvas. Encontrar el área del recinto determinado por dichas curvas.
5) Calcular el área de la región limitada por la curva de ecuación y = x(x - 1)(x - 2) y la recta de ecuación y = 0 . Hacer un dibujo de esta región.
6) Representar gráficamente el recinto plano limitado por la recta x - y = 1 y por la curva de ecuación
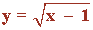
Calcular su área.
7) Calcular el área de la región limitada por las curvas:
y = x2 , y = x1/3
y las rectas:
x = -1 , x = 1
8) Dada la siguiente función
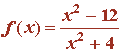
calcular el área de la región acotada encerrada por su gráfica y el eje OX.
9) Encontrar el área del recinto determinado por las siguientes curvas:
![]()
10) Representa gráficamente el recinto plano limitado por las curvas y = ex , y = e-x y por la recta x = 1 . Calcula su área.
11) Considera las funciones f : (0 , +∞) → R y g : R → R definidas,
f(x) = Ln x y g(x) = 1 - 2x ,
siendo Ln x el logaritmo neperiano de x . Calcula el área del recinto limitado por las rectas x = 1 y x = 2 y las gráficas de f y g .
12) a) Dibuja el recinto limitado por la curva y = 1/2 + cos x , los ejes de coordenadas y la recta x = π .
b) Calcula el área del recinto descrito en el apartado anterior.
13) Calcula el área del recinto limitado por la curva y = x - 2 sen x y las rectas y = 0 , x = -π/3 , x = π/3 . Haz un dibujo aproximado del recinto.
14) Haz un dibujo de la región limitada por la curva y = sen x cos x y las rectas x = 0 , x = 3π/2 , y = 0 . Calcula su área.
15) Representa la figura plana limitada por la gráfica de la función f(x) = cos x , en el intervalo -π/2 ≤ x ≤ π/2 , y la recta y = 1/2 . Calcula su área.
1) Calcular el área del recinto limitado por la gráfica de la función f(x) = x2 - 4 , el eje OX y la recta x = 3 .
La función f(x) es una parábola. Para dibujarla calcularemos sus puntos de corte con los ejes y su máximo o mínimo.
Puntos de corte con los ejes:
Si x = 0 : y = 02 - 4 = - 4 ⇒ (0 , 4)
Si y = 0 : x2 - 4 = 0 ⇒ x = ± 2 ⇒ (2 , 0) , (-2 , 0)
Máximo o mínimo:
f '(x) = 2x = 0 ⇔ x = 0
f ''(x) = 2 > 0
Como la segunda derivada siempre es positiva, la función tiene un mínimo en el punto x = 0.
Si x = 0 ⇒ y = -4 ⇒ Min (0 , -4)
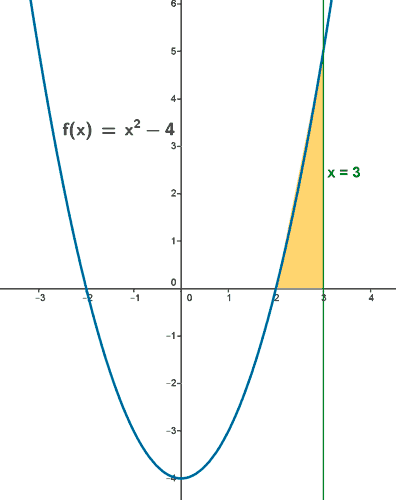
Si observamos la gráfica, el área que nos piden está delimitada desde x = 2 hasta x = 3. Por lo que tendremos que calcular una integral definida en dicho intervalo.
El área del recinto es la integral de la diferencia entre ambas funciones, es decir, de la función que "está arriba" menos la función que "está abajo".
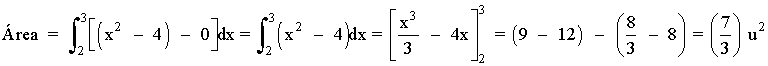
Calcular el área encerrada por la curva: y = x2 - 4x
y la recta: y = 2x - 5
Tenemos que dibujar una parábola y una recta. Para ello, vamos a calcular los puntos de corte con los ejes y los puntos de intersección entre ambas funciones, y el vértice de la parábola.
Puntos de corte con los ejes:
Si x = 0 :
y = x2 - 4x = 0 ⇒ (0 , 0)
y = 2x - 5 = -5 ⇒ (0 , -5)
Si y = 0 :
0 = x2 - 4x = x(x - 4) ⇒ x = 0 , x = 4 ⇒ (0 , 0) , (4 , 0)
0 = 2x - 5 ⇒ x = 5/2 ⇒ (5/2 , 0)
Vértice de la parábola:
xv = - b/2a = 4/2·1 = 2 ⇒ yv = 22 - 4·2 = - 4 ⇒ (2 , -4)
Intersección entre ambas funciones: resolvemos mediante igualación el sistema formado por las dos funciones.
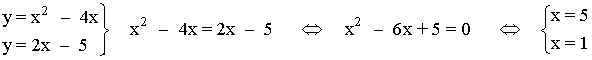
Sustituimos la solución en la ecuación más fácil, en este caso en la ecuación de la recta.
x = 5 ⇒ y = 2·5 - 5 = 5 ⇒ (5 , 5)
x = 1 ⇒ y = 2·1 - 5 = -3 ⇒ (5 , -3)
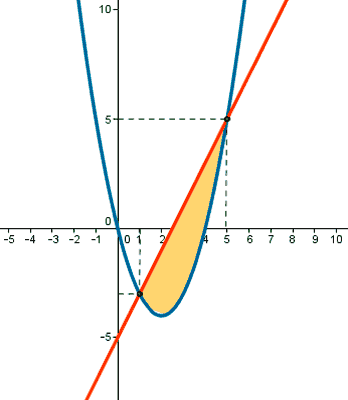
Si observamos la gráfica, el área del recinto está delimitado desde x = 1 hasta x = 5 . Por tanto, calcularemos su área mediante una integral definida en dicho intervalo.
El área del recinto es la integral de la diferencia entre ambas funciones, es decir, de la función que "está arriba" menos la función que "está abajo".
En este caso, es la integral de la ecuación de la recta menos la ecuación de la parábola.
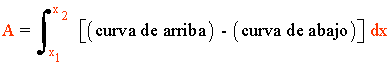
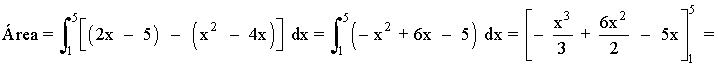
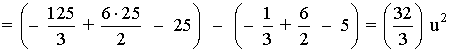
3) Determinar el área encerrada entre las gráficas de las funciones de ecuaciones:
y = 6x - x2 , y = x2 - 2x
Son ecuaciones de segundo grado, por lo que se tratan de parábolas. Para representarlas calculamos sus puntos de corte con los ejes, sus respectivos vértices y los puntos de intersección entre ambas.
Puntos de corte con los ejes:
Si x = 0 :
y = 6x - x2 = 0 ⇒ (0 , 0)
y = x2 - 2x = 0 ⇒ (0 , 0)
Si y = 0 :
0 = 6x - x2 = x(6 - x) ⇒ x = 0 , x = 6 ⇒ (0 , 0) , (6 , 0)
0 = x2 - 2x = x(x - 2) ⇒ x = 0 , x = 2 ⇒ (0 , 0) , (2 , 0)
Vértices:
y = 6x - x2 ⇒ xv = - b/2a = 6/2 = 3 ⇒ y = 6·3 - 32 = 9 ⇒ (3 , 9)
y = x2 - 2x ⇒ xv = -b/2a = 2/2 = 1 ⇒ y = 1 - 2 = -1 ⇒ (1 , -1)
Intersección entre ambas funciones: resolvemos mediante igualación el sistema formado por las dos funciones.
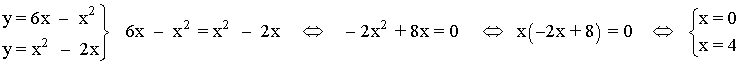
Sustituimos la solución en la ecuación más fácil, por ejemplo en la primera:
x = 0 ⇒ y = 0 ⇒ (0 , 0)
x = 4 ⇒ y = 6·4 - 42 =8 ⇒ (4 , 8)
La primera parábola tiene el término de mayor grado con signo negativo por lo que es convexa, y la segunda tiene signo positivo, por lo que es cóncava.
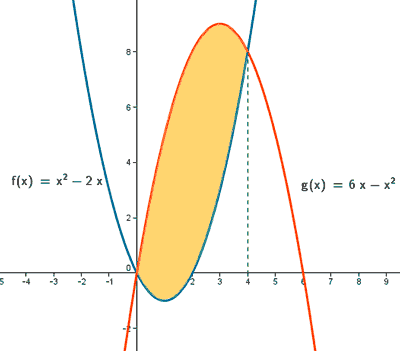
Si observamos la gráfica, el área del recinto está delimitado desde x = 0 hasta x = 4. Por tanto, calcularemos su área mediante una integral definida en dicho intervalo.
El área del recinto es la integral de la diferencia entre ambas funciones, es decir, de la función que "está arriba" menos la función que "está abajo".
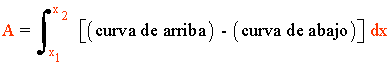
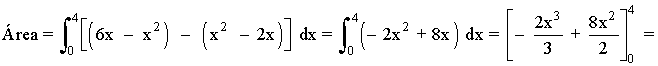
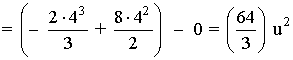
4) Se consideran, en el plano, las curvas de ecuaciones:

Dibujar estas curvas. Encontrar el área del recinto determinado por dichas curvas.
Ambas curvas son parábolas. Para representarlas calcularemos su puntos de corte con los ejes y sus respectivos vértices.
Puntos de corte con los ejes:
Si x = 0 :
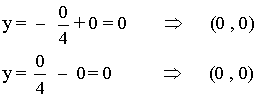
Si y = 0 :
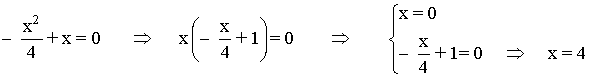
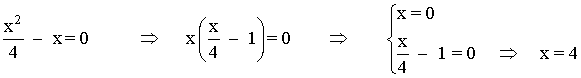
Ambas curvas tienen los mismos puntos de corte: (0 , 0) , (4 , 0)
Vértices:
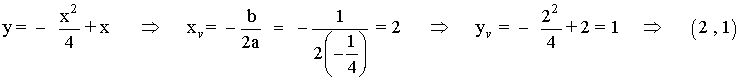
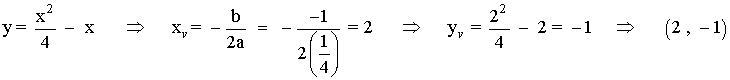
En la primera curva, el vértice (2 , 1) es un máximo puesto que a > 0 .
Y en la segunda, el vértice (2 , -1) es un mínimo puesto que a < 0 .
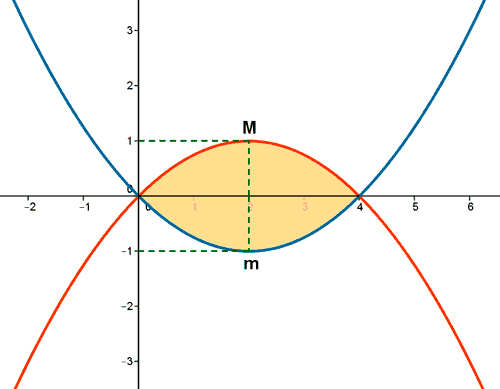
Si observamos la gráfica, el área que nos piden está delimitada desde x = 0 hasta x = 4. Por lo que tendremos que calcular una integral definida en dicho intervalo.
El área del recinto es la integral de la diferencia entre ambas funciones, es decir, de la función que "está arriba" menos la función que "está abajo".
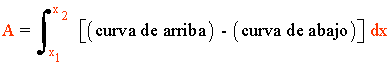
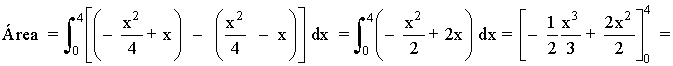
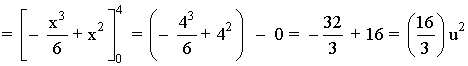
5) Calcular el área de la región limitada por la curva de ecuación y = x(x - 1)(x - 2) y la recta de ecuación y = 0 . Hacer un dibujo de esta región.
La recta de ecuación y = 0 se corresponde con el eje abscisas.
La ecuación de la curva es cúbica, para representarla calculamos sus puntos de corte, máximos, mínimos y puntos de inflexión.
Puntos de corte con los ejes:
Si x = 0 :
y = x(x - 1)(x - 2) = 0 ⇒ (0 , 0)
Si y = 0 :
0 = x(x - 1)(x - 2) ⇒ x = 0 , x = 1 , x = 2 ⇒ (0 , 0) , (1 , 0) , (2 , 0)
Máximos y mínimos:
f(x) = x(x -1)(x - 2) = x3 - 3x2 + 2x
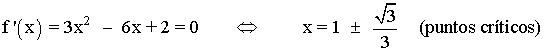
Vemos si son máximos o mínimos con la segunda derivada: f(x)'' = 6x - 6
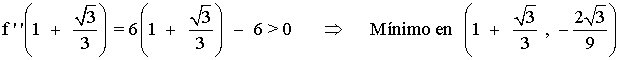
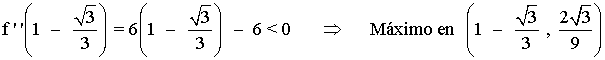
Puntos de inflexión:
f ''(x) = 6x - 6 = 0 ⇔ x = 6/6 = 1
f '''(x) = 6 ≠ 0
Por tanto, en x = 1 hay un punto de inflexión: (1 , 0)
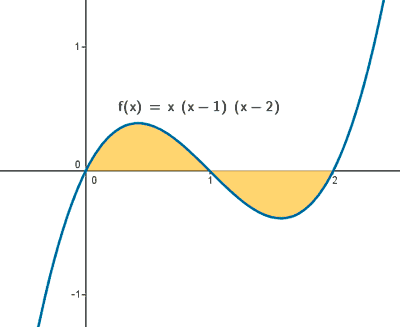
Si observamos la gráfica, el recinto está dividido en dos trozos, por lo que tendremos que calcular dos integrales. La primera integral estará definida desde x = 0 hasta x = 1 , y la segunda integral desde x = 1 hasta x = 2 .
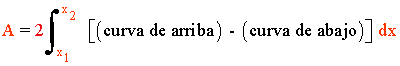
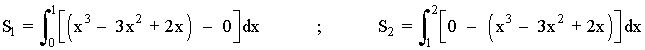
El área de cada trozo es la integral de la diferencia entre ambas funciones, es decir, de la función que "está arriba" menos la función que "está abajo".
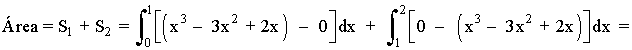
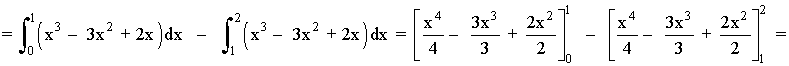
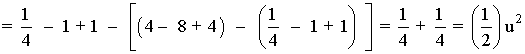
6) Representar gráficamente el recinto plano limitado por la recta x - y = 1 y por la curva de ecuación
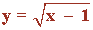
Calcular su área.
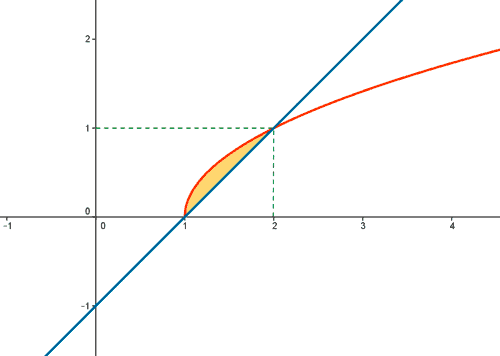
La ecuación de la recta se puede escribir: x - y = 1 ⇒ y = x - 1
El recinto está delimitado por los puntos de intersección entre ambas funciones, por lo que tenemos que calcularlos. Para ello, igualamos ambas ecuaciones:
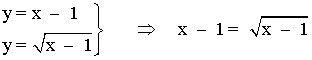
![]()
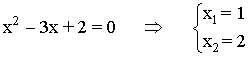
Sustituimos en cualquiera de las ecuaciones:
Si x = 1 ⇒ y = x - 1 = 1 - 1 = 0 ⇒ (1 , 0)
Si x = 2 ⇒ y = x - 1 = 2 - 1 = 1 ⇒ (2 , 1)
El área que nos piden está delimitada desde x = 1 hasta x = 2. Por lo que tendremos que calcular una integral definida en dicho intervalo.
El área del recinto es la integral de la diferencia entre ambas funciones, es decir, de la función que "está arriba" menos la función que "está abajo".
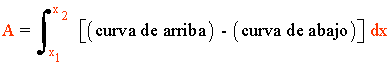
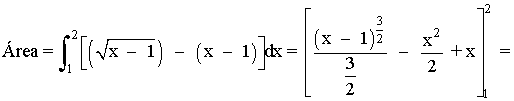
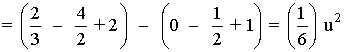
7) Calcular el área de la región limitada por las curvas:
y = x2 , y = x1/3
y las rectas:
x = -1 , x = 1
La curva y = x2 es una parábola con vértice en el punto (0,0) , que coincide con el punto de corte con los ejes.
Las rectas x = -1 , x = 1 son rectas verticales que cortan al eje X en los puntos: (-1,0) ,(1,0)
Para poder dibujar la curva y = x1/3 tenemos que hacer un pequeño estudio:
Puntos de corte con los ejes: x = 0 ⇒ y = 0 ⇒ (0 , 0)
Crecimiento, decrecimiento y convexidad: como el recinto está delimitado por x = -1 , x = 1 haremos el estudio en el intervalo [-1 , 1]
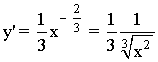
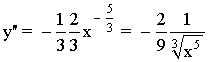
Observamos que ambas derivadas no están definidas en x = 0 por lo que consideramos los intervalos:
[-1 , 0) , (0 , 1]
| [-1 , 0) | (0 , 1] | |
|---|---|---|
| y' | y' > 0 creciente |
y' > 0 creciente |
| y'' | y'' > 0 cóncava |
y' < 0 convexa |
Como no hay cambio de monotonía, el punto x = 0 no es ni máximo ni mínimo.
Sin embargo, sí hay un cambio de curvatura, por lo que el punto x = 0 es punto de inflexión.
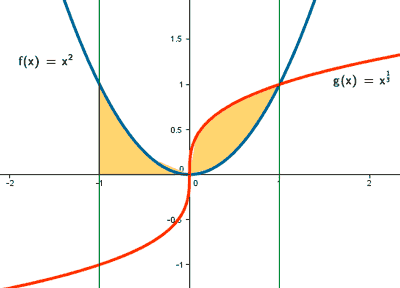
El área que tenemos que calcular está dividida en dos trozos, por lo que tendremos que calcular dos integrales: S1 , S2
El primer trozo lo calculamos con una integral definida desde x = -1 hasta x = 0 , y el segundo, con otra integral definida desde x = 0 hasta x = 1.
En cada trozo, el área será la integral de la diferencia entre ambas funciones, es decir, de la función que "está arriba" menos la función que "está abajo".
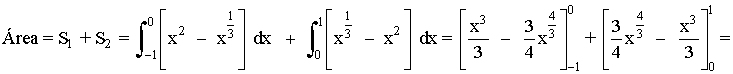
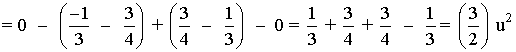
8) Dada la siguiente función
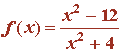
calcular el área de la región acotada encerrada por su gráfica y el eje OX.
Para calcular el área de una región es útil hacer, cuando es posible, un esbozo de dicha región. Vamos pues a estudiar la función f para hacer dicho esbozo.
Puntos de corte:
Si x=0
![]()
Si y=0
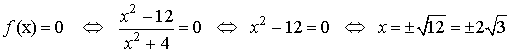
Máximos y mínimos:
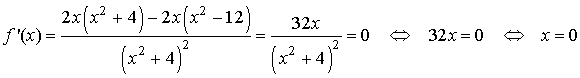
El crecimiento de la función se estudia en la siguiente tabla
| (-∞ , 0) | (0 ,∞ ) | |
|---|---|---|
| y' | y' < 0 decreciente |
y' > 0 creciente |
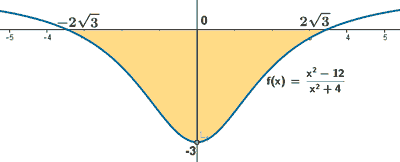
Y el mínimo de la función se encuentra en x=0.
Si observamos la gráfica, el área que nos piden está delimitada desde x = -2√3 hasta x = 2√3 . Por lo que tendremos que calcular una integral definida en dicho intervalo. El área del recinto es la integral de la diferencia entre ambas funciones, es decir, de la función que "está arriba", el eje OX , menos la función que "está abajo".
Simetría:
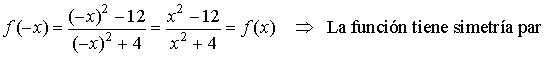
Teniendo en cuenta la simetría de la función y que es negativa:
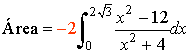
El signo menos se debe a que la función queda por debajo del eje OX y el 2 por la simetria par.
Haciendo la división de polinomios:
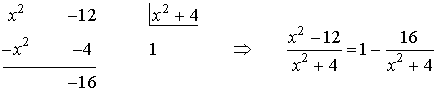
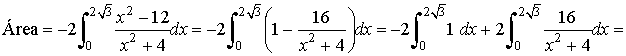
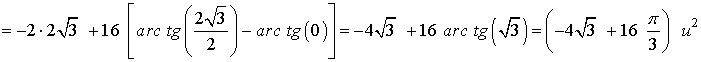
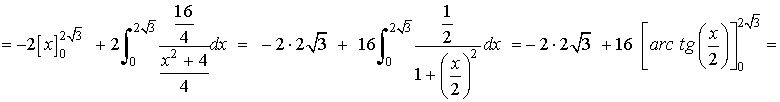
9) Encontrar el área del recinto determinado por las siguientes curvas:
![]()
Vamos a esbozar la gráfica de ambas curvas.
Puntos de corte:
Para la primera curva si x = 0 obtenemos y = 2 → (0,2) y si y = 0 no hay solución.
Para la segunda curva si x = 0 obtenemos y = 0 → (0,0) y si y = 0 obtenemos x = 0 →(0,0)
Intersección de las dos curvas:
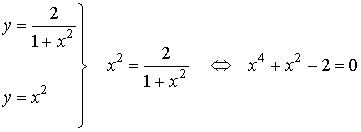
Observamos que esta ecuación es bicuadrada, de manera que se resuelve empleando el cambio de variable t = x2, con el cual obtenemos la ecuación t2+ t -2 = 0, cuyas raíces son t = -2 y t = 1. Deshaciendo el cambio de variable las raíces reales de dicha ecuación resultan ser x = 1 y x= -1.
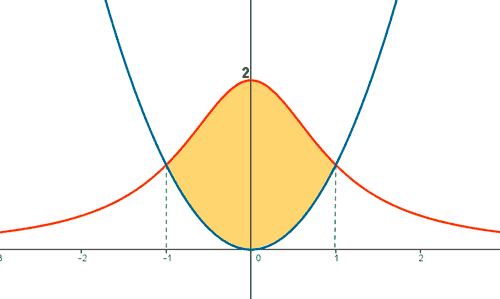
Como las curvas se cortan en x = -1 y x = 1, integraremos entre x = -1 y x = 1.
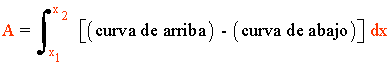
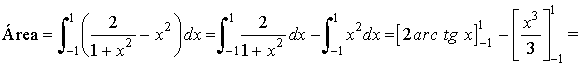
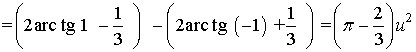
10) Representa gráficamente el recinto plano limitado por las curvas y = ex , y = e-x y por la recta x = 1 . Calcula su área.
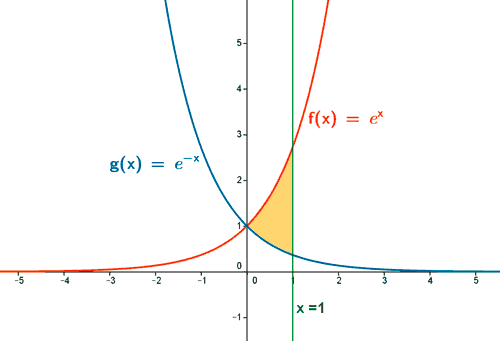
El recinto está delimitado por la izquierda por el punto de intersección entre ambas funciones, así que vamos a calcularlo:
ex = e-x ⇔ x = - x ⇔ x = 0
Si x = 0 ⇒ y = e0 = 1 ⇒ (0 , 1)
Por tanto, el área que nos piden está delimitada desde x = 0 hasta x =1, luego tendremos que calcular una integral definida en dicho intervalo.
El área del recinto es la integral de la diferencia entre ambas funciones, es decir, de la función que "está arriba" menos la función que "está abajo".
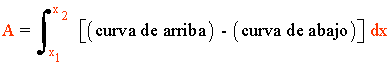
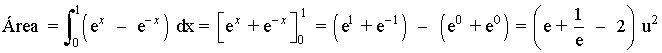
11) Considera las funciones f : (0 , +∞) → R y g : R → R definidas,
f(x) = Ln x y g(x) = 1 - 2x ,
siendo Ln x el logaritmo neperiano de x . Calcula el área del recinto limitado por las rectas x = 1 y x = 2 y las gráficas de f y g .
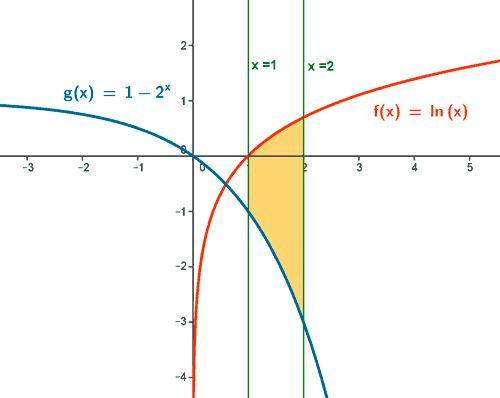
Si observamos la gráfica, el área que nos piden está delimitada desde x = 1 hasta x = 2. Por lo que tendremos que calcular una integral definida en dicho intervalo.
El área del recinto es la integral de la diferencia entre ambas funciones, es decir, de la función que "está arriba" menos la función que "está abajo".
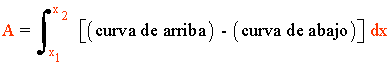
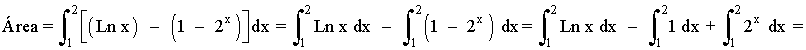
Calculamos la integral del logaritmo por separado, aplicando integración por partes:
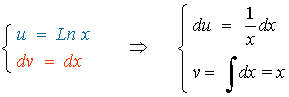
![]()
Terminamos de calcular el área:
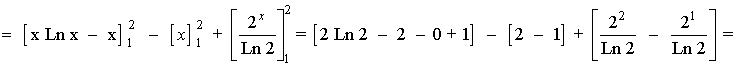
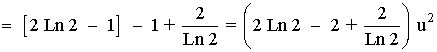
12) a) Dibuja el recinto limitado por la curva y = 1/2 + cos x , los ejes de coordenadas y la recta x = π .
b) Calcula el área del recinto descrito en el apartado anterior.
Observamos que la curva es una traslación hacia arriba de la función coseno. Vamos a calcular el punto de corte de la función con el eje X :
1/2 + cos x = 0 ⇔ cos x = -1/2 ⇔ x = 2π/3
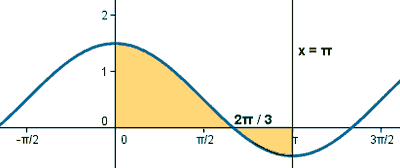
El recinto ha quedado dividido en dos trozos, por lo que calcularemos su área mediante dos integrales.
El primer trozo lo calculamos con una integral definida desde x = 0 hasta x = 2π/3 , y el segundo, con otra integral definida desde x = 2π/3 hasta x = π .
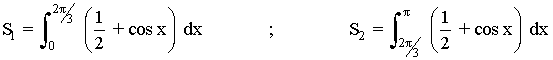
Como en el segundo trozo la función está por debajo del eje X, tendremos que restar su integral.
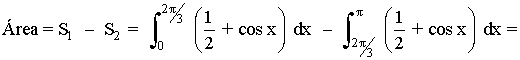
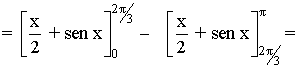
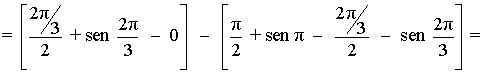
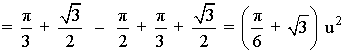
13) Calcula el área del recinto limitado por la curva y = x - 2 sen x y las rectas y = 0 , x = -π/3 , x = π/3 . Haz un dibujo aproximado del recinto.
Para poder representar la curva vamos a hacer un pequeño estudio. Como el recinto está delimitado por las rectas x = -π/3 , x = π/3 , sólo tenemos que estudiar la función en el intervalo (-π/3 , /π/3).
Máximos y mínimos:
f '(x) = 1 - 2 cos x = 0 ⇔ cos x = 1/2 ⇔ x = π/3 , x = -π/3
| Intervalo | (-π/3, π/3) |
|---|---|
| Punto de prueba | f ' (0) < 0 |
| Signo de f ' (x) | - |
| Monotonía | Decrece |
Podemos comprobar si son máximos o mínimos con la segunda derivada: f ''(x) = 2 sen x
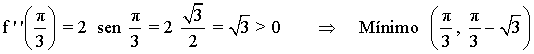
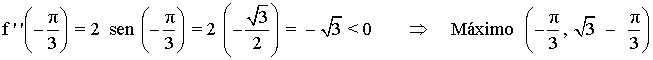
Puntos de inflexión:
f ''(x) = 2 sen x = 0 ⇔ sen x = 0 ⇔ x = 0
| Intervalo | (-π/3 , 0) | ( 0 , π/3) |
|---|---|---|
| Punto de prueba | f '' (- π/4) < 0 | f '' ( π/4) > 0 |
| Signo de f '' (x) | - | + |
| Curvatura | Convexa (∩) | Cóncava (∪) |
Podemos comprobar si x = 0 es punto de inflexión con la derivada tercera:
f '''(x) = 2 cos x ⇒ f '''(0) = 2 cos 0 = 2 ≠ 0 ⇒ x = 0 es punto de inflexión
La función es simétrica impar:
![]()
Por lo tanto, el área entre las rectas x = -π/3 y x = π/3 es el doble del área entre las rectas x = - π/3 y x = 0
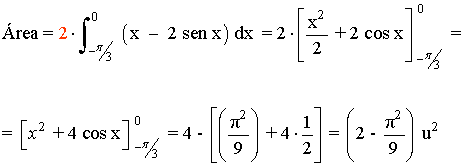
Otra forma de calcular el área
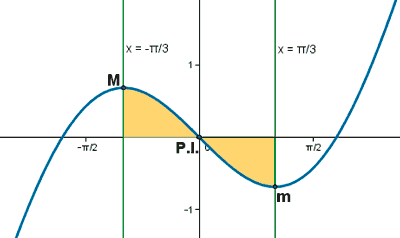
Si observamos la gráfica, el área que nos piden está delimitada desde x = -π/3 hasta x = π/3 , y está dividia en dos trozos, por lo que tendremos que calcular dos integrales.
El área de cada trozo es la integral de la diferencia entre ambas funciones, es decir, de la función que "está arriba" menos la función que "está abajo".
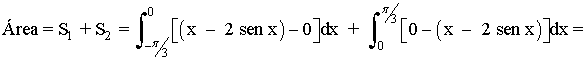
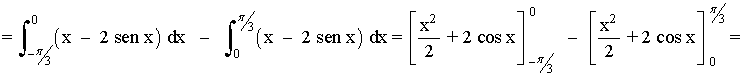
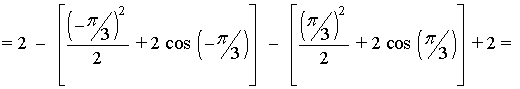
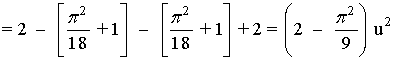
14) Haz un dibujo de la región limitada por la curva y = sen x cos x y las rectas x = 0 , x = 3π/2 , y = 0 . Calcula su área.
Para poder representar la curva hacemos previamente un pequeño estudio. Como la curva está delimitada por las rectas x = 0 , x = 3π/2 , tendremos que estudiarla en el intervalo [0 , 3π/2].
Aplicando la fórmula trigonométrica del ángulo doble tenemos la función queda:
![]()
Calculamos los puntos de corte que hayan dentro del intervalo [0 , 3π/2].
Puntos de corte con el eje Y:
![]()
Puntos de corte con el eje X:
![]()
![]()
![]()
![]()
sen(-x) = - sen x
Monotonia: crecimiento y decrecimiento
Se halla la derivada primera, se iguala a 0 y se estudia su signo en los intervalos obetenidos:
f '(x) = 1/2 · 2 · cos (2x) = cos (2x) = 0 ⇔ 2x = π/2 ó 2x = 3π/2 ó 2x = 5π/2 ⇔ x = π/4 ó x = 3π/4 ó x = 5π/4
Estudiaremos sólo aquellos puntos que estén dentro del período de la función: (0, π/4) , (π/4, 3π/4) , (3π/4, 5π/4) , (5π/4, 3π/2)
| Intervalo | (0 , π/4) | (π/4 , 3π/4) | (3π/4, 5π/4) | (5π/4, 3π/2) |
|---|---|---|---|---|
| Punto de prueba | f ' ( π/6) > 0 | f ' (π/2) < 0 | f ' ( π) > 0 | f ' ( 4π/3) > 0 |
| Signo de f ' (x) | + | - | + | - |
| Monotonía | Crece | Decrece | Crece | Decrece |
Por el apartado anterior sabemos que los puntos críticos o puntos que anulan a la derivada primera son x = π/4 , x = 3π/4 y x = 5π/4 , vamos a determinar a través de la segunda derivada si se tratan de máximos o mínimos.
Hallamos la derivada segunda: f '' (x) = 2 (- sen 2x) = - 2 sen(2x)
• f '' ( π/4) = - 2 < 0 ⇒ Hay un máximo en x = π/4 ⇒ f(π/4) = 1/2 ⇒ Max (π/4, 1/2)
• f '' (3π/4) = 2 > 0 ⇒ Hay un mínimo en x = 3π/4 ⇒ f(3π/4) = - 1/2 ⇒ Min (3π/4, -1/2)
• f '' (5π/4) = -2 < 0 ⇒ Hay un máximo en x = 5π/4 ⇒ f(5π/4) = 1/2 ⇒ Max (5π/4, 1/2)
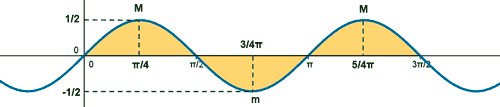
Como la función tiene simetría impar, el área de los tres trozos es igual, por lo que basta con calcular una única integral y multiplicarla por tres.
sen(-x) = - sen x
Tomamos como referencia el área del primer trozo, que está delimitado por x = 0 y x = π/2 .
El área del recinto es la integral de la diferencia entre ambas funciones, es decir, de la función que "está arriba" menos la función que "está abajo".
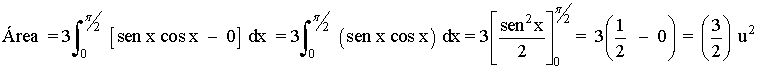
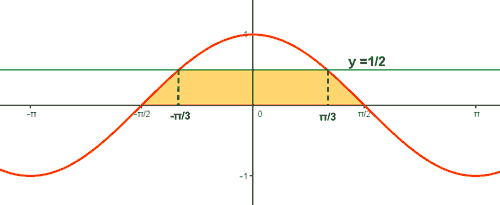
15) Representa la figura plana limitada por la gráfica de la función f(x) = cos x , en el intervalo -π/2 ≤ x ≤ π/2 , y la recta y = 1/2 . Calcula su área.
Sabemos que la función coseno corta al eje OX en los puntos: (-π/2 , 0) , (π/2 , 0)
Calculamos la intersección entre f(x) y la recta y = 1/2 :
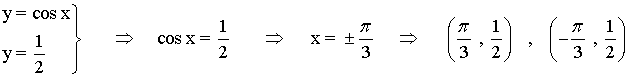

Para calcular el área del recinto vamos a considerar:
• El área del rectángulo que va desde x=-π/3 hasta x = π/3 .La calcularemos con su correspondiente fórmula del área.
• Las áreas de los dos "triángulos" que han quedado en los extremos. Como sus áreas son iguales, bastará calcular una única integral y multiplicarla por dos.
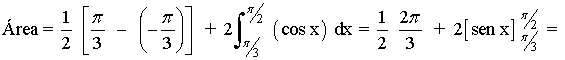
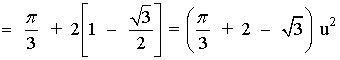


 INICIO
INICIO