Problemas resueltos de áreas IV: Funciones a trozos y con valor absoluto
1) Sea f : IR → IR la función definida por
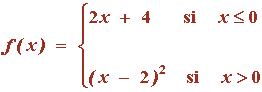
(a) Calcula los puntos de corte de la gráfica de f con el eje de abscisas y esboza dicha gráfica.
(b) Halla el área de la región acotada que está limitada por la gráfica de f y por el eje de abscisas.
2) Sea f : IR → IR la función definida por
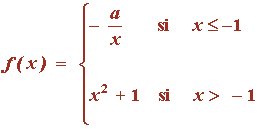
(a) Halla el valor de a sabiendo que f es continua
(b) Esboza la gráfica de f.
(c) Calcula el área del recinto limitado por la gráfica de f, el eje de abscisas y las rectas x + 2 = 0 y x - 2 = 0
3) Calcúlese el área delimitada por la gráfica de
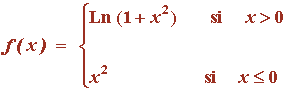
y las rectas x = -1, x = 1, y = 0.
4) Calcular el área del recinto limitado por la curva de ecuación f(x) = | x2 -4 | y las rectas x = -1, x = 4 e y = 0.
5) Halla el área de la región limitada por la gráfica de la función
f(x) = |(x - 1)(3x - 1)|
el eje X, el eje Y y la recta x = 2.
6) Sea f:IR→IR la función definida por f(x) =x |x - 2|
(a) Esboza la gráfica de f.
(b) Calcula el área del recinto limitado por la gráfica de f el eje de abscisas
7) Sea f:IR→IR la función definida por f(x) =x |x|
(a) Dibuja la región acotada del plano que está limitada por la gráfica de f y la bisectriz del primer y tercer cuadrante.
(b) Calcula el área de la región descrita en el apartado anterior.
8)
(a) Dibuja el recinto limitado por las curvas y = |x| - 1 e y = 1 - |x|
(b) Hallar el área de dicho recinto
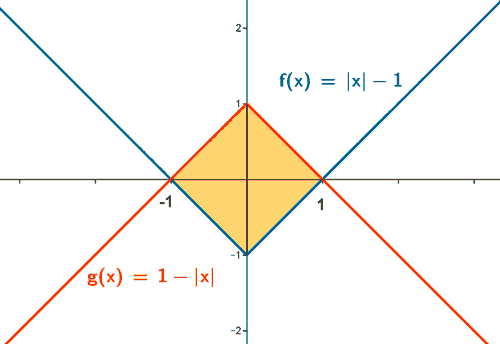
9)
(a) Dibujar el recinto limitado por la curva y = |x + 1| + |x| y por la recta y = 3.
(b) Calcular el área de dicho recinto mediante integración y comprobar el resultado, calculando el área de esa figura elemental.
1) Sea f : IR → IR la función definida por
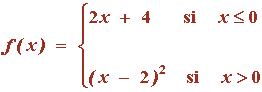
(a) Calcula los puntos de corte de la gráfica de f con el eje de abscisas y esboza dicha gráfica.
(b) Halla el área de la región acotada que está limitada por la gráfica de f y por el eje de abscisas.
(a)
Puntos de corte con el eje de abscisas
Para y=0, tenemos que
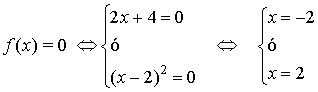
de manera que los puntes de corte con el eje de abscisas son ( -2 , 0 ) y ( 2 , 0 ).
Para x=0, tenemos que
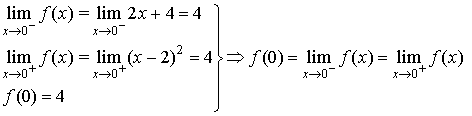
de manera que f es continua en 0.
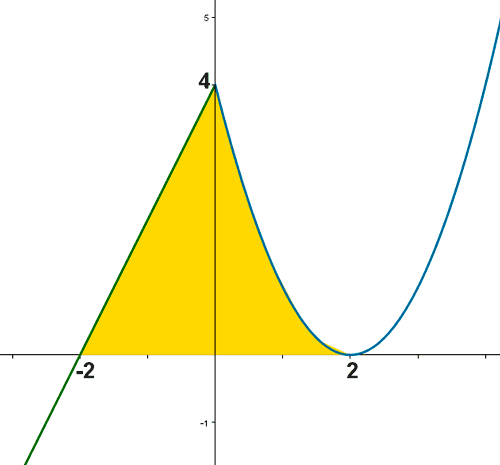
(b)
A la vista del esbozo que hemos dado en el apartado anterior, podemos calcular el área que se nos pide como sigue:
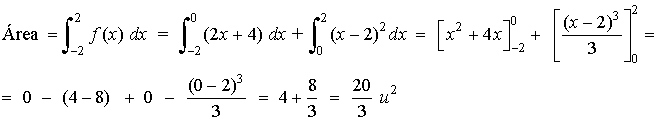
2) Sea f : IR → IR la función definida por
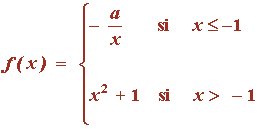
(a) Halla el valor de a sabiendo que f es continua
(b) Esboza la gráfica de f.
(c) Calcula el área del recinto limitado por la gráfica de f, el eje de abscisas y las rectas x + 2 = 0 y x - 2 = 0
(a)
Por la continuidad de f en x = -1, podemos obtener que
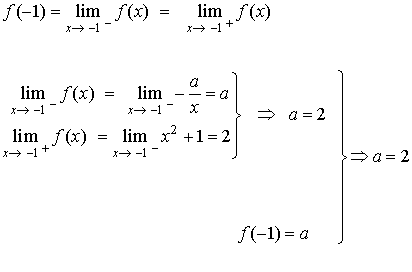
y f queda definida como
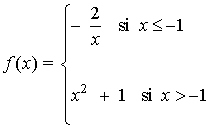
(b)
La primera rama de la función es una función estrictamente creciente para todo x ≤ -1, tiene límite 0 cuando x→-∞ y además f( -1) = 2.
La segunda rama es una parábola cuyo mínimo es ( 0, 1 ). Además f( -1 ) = 2.
Teniendo en cuenta lo anterior podemos dar el esbozo de la función:
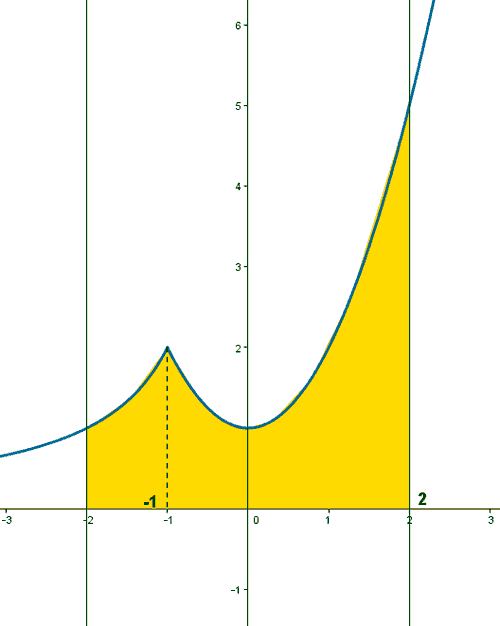
(c)
A la vista del gráfico de la función, vemos que para calcular el área tenemos que integrar entre -2 y -1 la primera rama de la función y entre -1 y 2 la segunda rama:
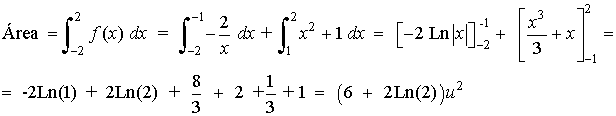
3) Calcúlese el área delimitada por la gráfica de
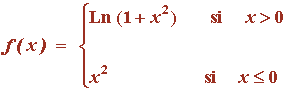
y las rectas x = -1, x = 1, y = 0.
Esbozo gráfica
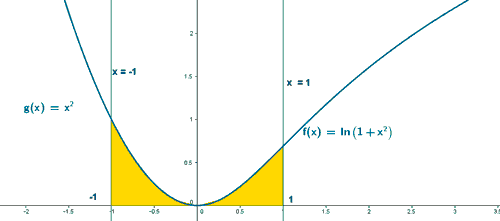
A la vista de la gráfica, queda claro que tenemos que integrar entre -1 y 0 la primera rama de la función y entre 0 y 1 la segunda rama.
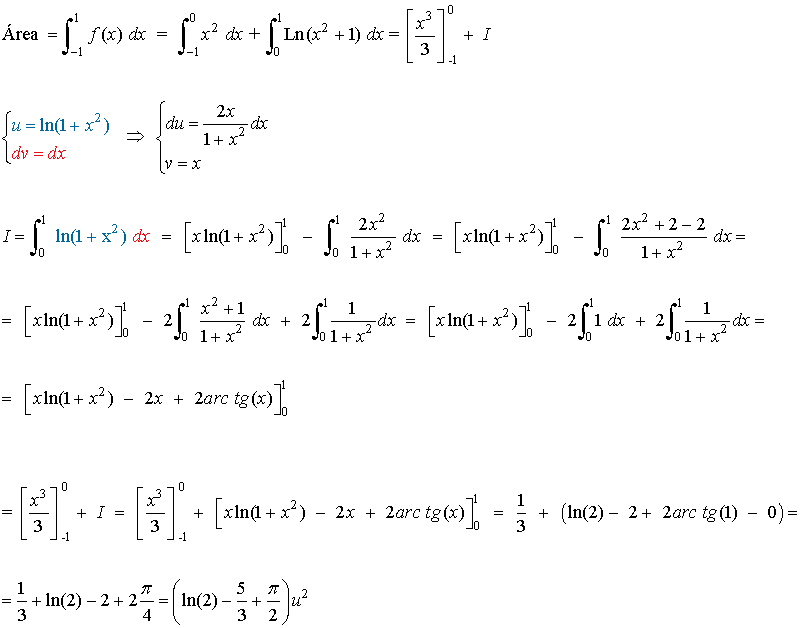
4) Calcular el área del recinto limitado por la curva de ecuación f(x) = | x2 -4 | y las rectas x = -1, x = 4 e y = 0.
Puntos de corte con el eje X
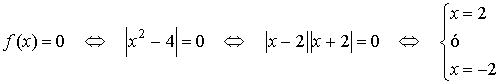
| Intervalo | (- ∞, -2) | (-2,2) | (2, +∞) |
|---|---|---|---|
| Punto de prueba | f(-4) > 0 | f(0) < 0 | f(4) > 0 |
| | (x + 2)(x - 2) | | (x + 1)(x - 1) | - (x + 2)(x - 2) | (x + 2)(x - 2) |
Teniendo esto en cuenta, podemos expresar a f como función definida a trozos:
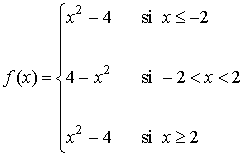
y la gráfica resulta ser la siguiente:
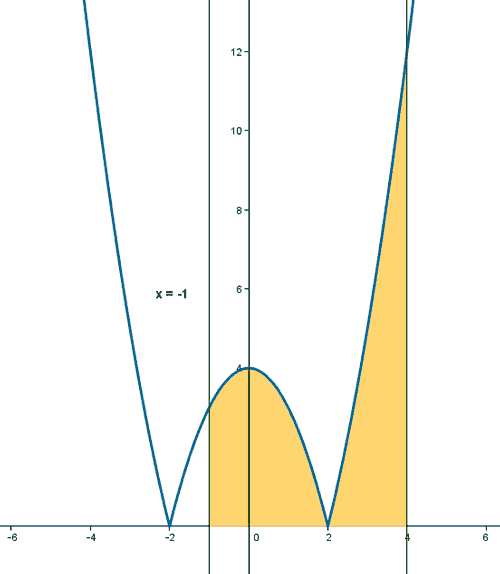
A la vista de la definición de f como función definida a trozos y de su gráfica, es fácil calcular el área que se nos pide. Entre -1 y 2 tendremos que integrar la segunda rama y entre 2 y 4 tendremos que integrar la tercera rama:
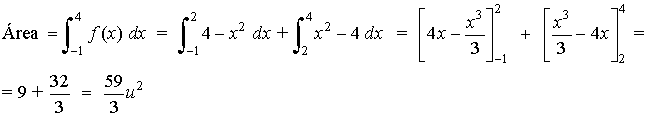
5) Halla el área de la región limitada por la gráfica de la función
f(x) = |(x - 1)(3x - 1)|
el eje X, el eje Y y la recta x = 2.
Puntos de corte con el eje X
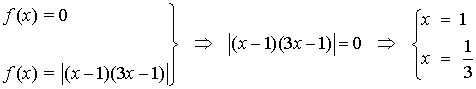
| Intervalo | (- ∞, 1) | (1/3, 1) | (1, +∞) |
|---|---|---|---|
| Punto de prueba | f(0) > 0 | f(1/2) < 0 | f(3) > 0 |
| | (x - 1)(3x - 1) | | (3x - 1)(x - 1) | - (3x - 1)(x - 1) | (3x - 1)(x - 1) |
Teniendo esto en cuenta, podemos expresar a f como función definida a trozos como sigue:
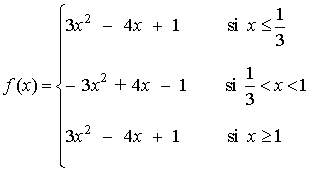
Teniendo en cuenta lo anterior, podemos representar gráficamente la función:
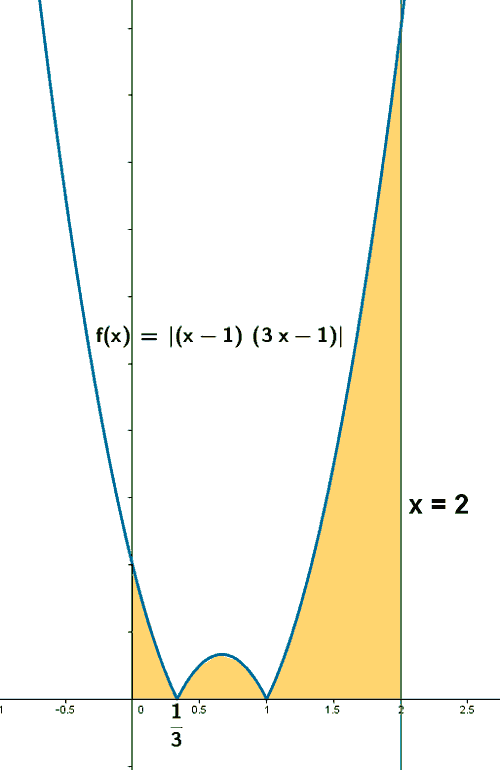
A la vista de la definición de f como función definida a trozos y de su gráfica, es fácil calcular el área que se nos pide. Entre 0 y 1/3 tendremos que integrar la primera rama entre 1/3 y 1 tendremos que integrar la segunda rama y entre 1 y 2 la tercera:
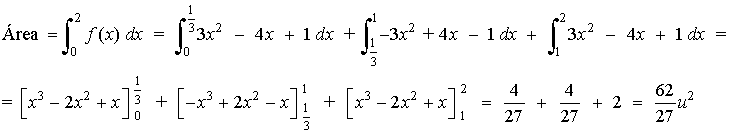
6) Sea f:IR→IR la función definida por f(x) =x |x - 2|
(a) Esboza la gráfica de f.
(b) Calcula el área del recinto limitado por la gráfica de f el eje de abscisas
(a)
Puntos de corte con el eje X
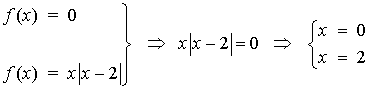
| Intervalo | (- ∞, 0) | (0, 2) | (2, +∞) |
|---|---|---|---|
| Punto de prueba | f(-1) < 0 | f(1) < 0 | f(3) > 0 |
| x| x - 2 | | x(2-x) | x(2-x) | x(x-2) |
Teniendo esto en cuenta, podemos expresar a f como función definida a trozos como sigue:
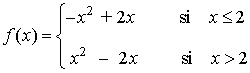
Teniendo en cuenta lo anterior, podemos representar gráficamente la función:
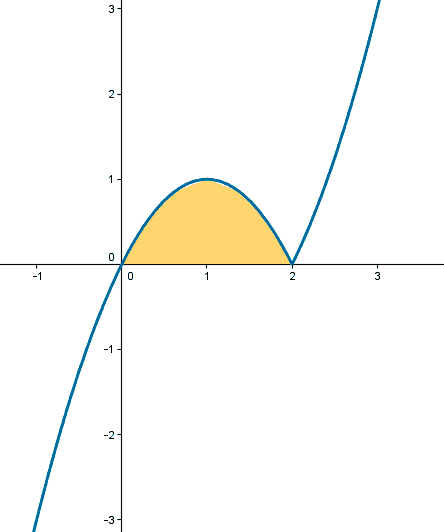
(b)
A la vista de la definición de f como función definida a trozos y de su gráfica, es fácil calcular el área que se nos pide. Bastará con integrar la primera rama entre 0 y 2.
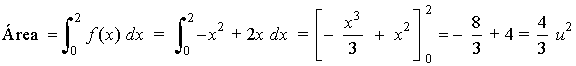
7) Sea f:IR→IR la función definida por f(x) =x |x|
(a) Dibuja la región acotada del plano que está limitada por la gráfica de f y la bisectriz del primer y tercer cuadrante.
(b) Calcula el área de la región descrita en el apartado anterior.
(a)
Puntos de corte con el eje X de la función f
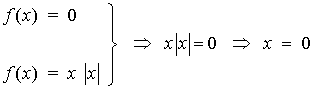
| Intervalo | (- ∞, 0) | (0, +∞) |
|---|---|---|
| Punto de prueba | f(-1) < 0 | f(1) > 0 |
| x|x| | -x · x | x · x |
Teniendo esto en cuenta, podemos expresar a f como función definida a trozos como sigue:
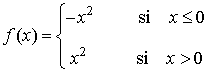
Intersección de f y la bisectriz del primer y tercer cuadrante y = x
Obtenemos primero las abscisas en que se intersecan f y la recta y = x:
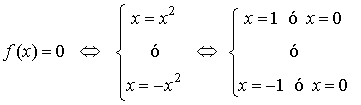
Teniendo en cuenta todo lo anterior, podemos representar gráficamente el área que nos pedían calcular:
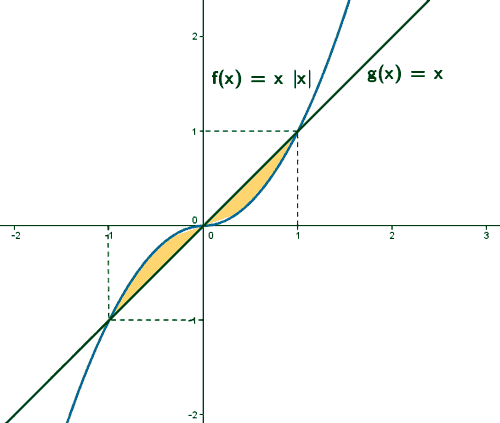
(b)
A la vista de la gráfica el área que se nos pide se calcula como sigue:
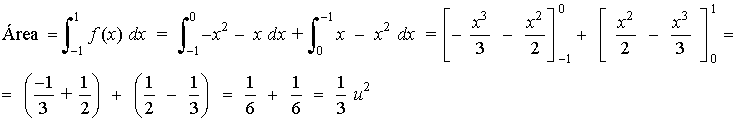
8)
(a) Dibuja el recinto limitado por las curvas y = |x| - 1 e y = 1 - |x|
(b) Hallar el área de dicho recinto
(a)
Sabemos que
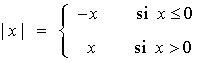
de manera que es claro que las curvas admiten las siguientes expresiones a trozos:

A la vista de estas expresiones, la gráfica obtenida es la siguiente:
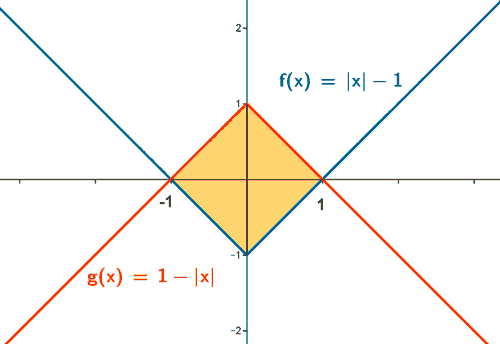
Y el recinto que nos piden dibujar es el que aparece sombreado
(b)
Observamos que ambas curvas son pares. En efecto,
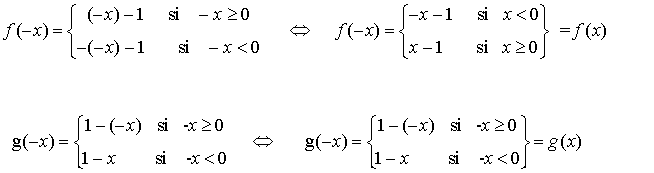
de manera que basta con que integremos entre 0 y 1. Por tanto, el área es
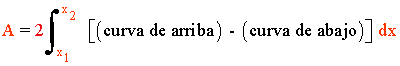
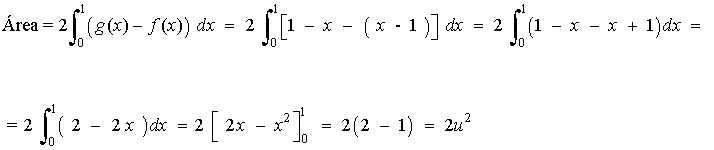
9)
(a) Dibujar el recinto limitado por la curva y = |x + 1| + |x| y por la recta y = 3.
(b) Calcular el área de dicho recinto mediante integración y comprobar el resultado, calculando el área de esa figura elemental.
(a)
Empezamos viendo que
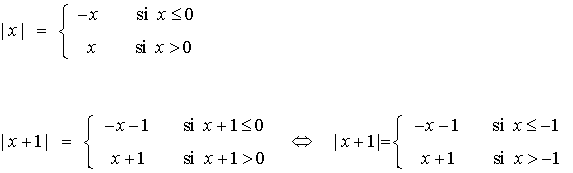
Teniendo esto en cuenta
| Intervalo | (- ∞, -1) | (-1, 0) | (0, +∞) |
|---|---|---|---|
| |x| | -x | -x | x |
| |x+1| | -x-1 | x+1 | x+1 |
| |x|+|x+1| | -2x-1 | 1 | 2x+2 |
por lo cual obtenemos que
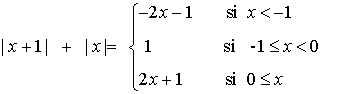
Calculamos ahora las intersecciones de la curva con la recta y = 3
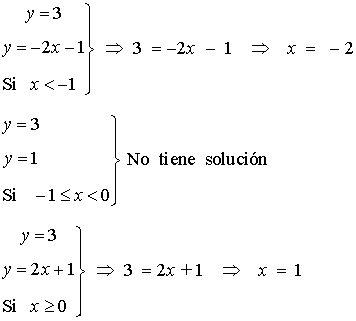
De manera que los puntos de intersección son ( -2, 3 ) y ( 1, 3 )
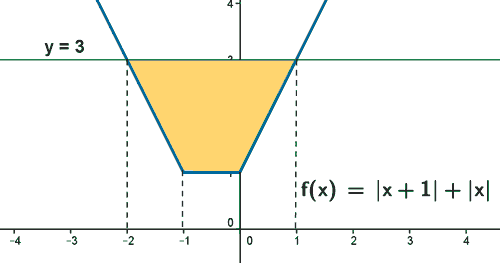
Teniendo en cuenta todo lo anterior, la gráfica resulta ser la siguiente:
(b)
A la vista de la gráfica y de la expresión de la función, el área se calculará como sigue:
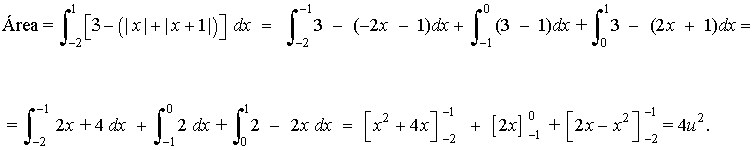
Observando la gráfica, se aprecia fácilmente que el recinto cuya área queremos calcular es un trapecio. Su base menor tiene longitud b = 1, su base mayor tiene longitud B = 4 y su altura es h=2. Por tanto:
![]()


 INICIO
INICIO