Problemas resueltos de Áreas III: En función de y
1) Hallar el área de la región limitada por el eje de ordenadas, la recta y = 3 y la curva y = ex
2) Hallar el área de la región limitada por el eje de ordenadas, la curva
![]()
y las rectas y = 2, y = 4.
3) Hallar el área limitada por la parábola y2 = 4 - x y el eje de ordenadas.
4) Hallar el área del recinto limitado por la curva y2 + 2y + x - 3 = 0 y la recta y= 4x + 1
5) Determinar el área del recinto limitado por la parábola
y 2 = 2x
y la recta que une los puntos ( 2, -2 ) y ( 4, 2√2 )
6) Hallar el área encerrada por
y2+ 2y + x - 3 = 0 e y = x + 1
7) Hallar el área limitada por las curvas y2 = 4x ; y2 = x + 3.
1) Hallar el área de la región limitada por el eje de ordenadas, la recta y = 3 y la curva y = ex
Empezamos esbozando la curva y = ex. Observamos primero que y' = ex, y'' = ex >0 de manera que la función es convexa. Por otra parte si x = 0, entonces y = 1.
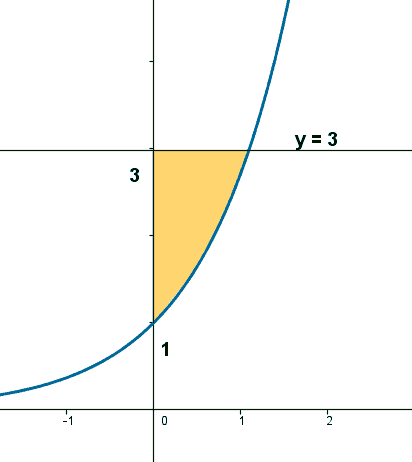
A la vista de la gráfica, es claro que tendremos que integrar sobre el eje de ordenadas entre 1 y 3. La función que tendremos que considerar será la inversa de y = ex, es decir, integraremos la función x = log y. Por tanto, el área que se nos piden se calculará como sigue:
de es la siguiente:
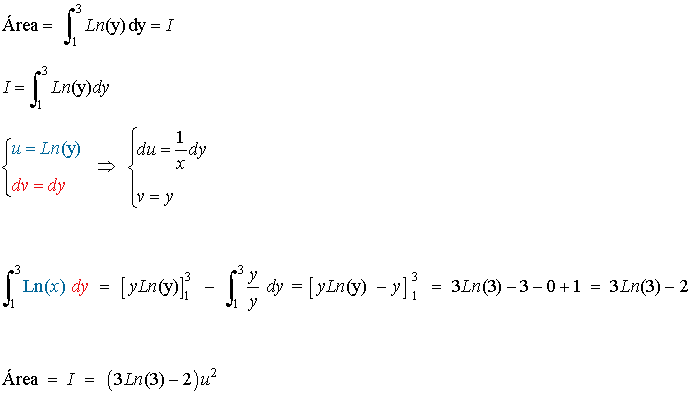
2) Hallar el área de la región limitada por el eje de ordenadas, la curva
![]()
y las rectas y = 2, y = 4.
Empezamos esbozando la gráfica. Por su forma vemos que es una hipérbola equilátera. Igualando el denominador a 0 obtenemos que x = -2 es la asíntota vertical de la curva.
Por otra parte
![]()
de manera que y = 1 es la asíntota horizontal de la curva. Podemos ahora despejar x obteniendo la exprresión de la curva con y como variable independiente:
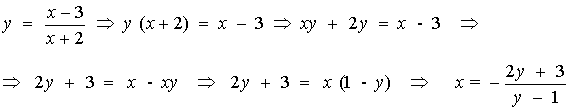
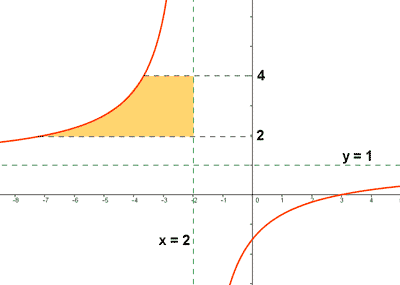
A la vista de la gráfica, vemos que bastará con integrar tomando y como variable independiente para y entre 2 y 4:
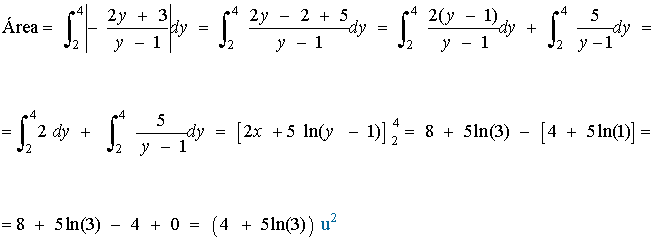
3) Hallar el área limitada por la parábola y2 = 4 - x y el eje de ordenadas.
Puntos de corte
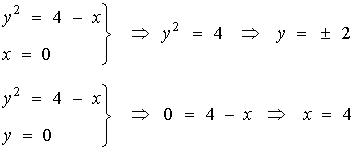
De manera que los puntos de corte son ( 0, 2 ) , ( 0, -2 ) con el eje de ordenadas y ( 4, 0 ) con el eje de abscisas.
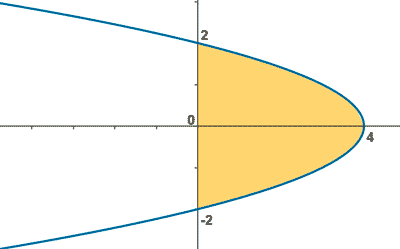
A la vista de la gráfica el área, vemos que nos interesa integrar respecto de y , de manera que:
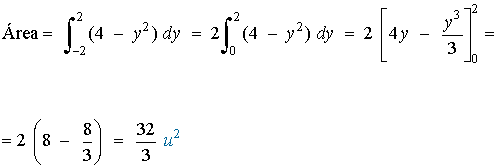
4) Hallar el área del recinto limitado por la curva y2 + 2y + x - 3 = 0 y la recta y= 4x + 1
Por la forma que tiene la primera ecuación, para evitar tener que trabajar con radicales al despejar a la incognita y, resulta más conveniente utilizar a y como variable independiente. Despejando x, podemos expresar las ecuaciones como sigue:
![]()
Resolviendo el sistema de ecuaciones:
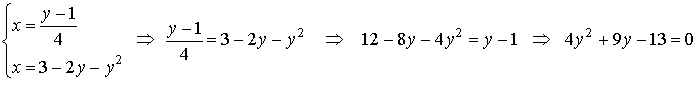
obtenemos que los puntos de corte son los que tienen
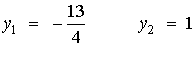
Si derivamos la primera ecuación, obtenemos que x' = -2 - 2y. Igualando a 0, -2 -2y = 0 si y sólo si y = -1. Derivando de nuevo, obtenemos que x'' = -2, de manera que en y = -1 la parábola alcanza su máximo, es decir, su vértice (4,-1). Esto nos dice que en y = -1 la parábola alcanza su valor máximo de x, que es 4.
Puntos de corte
Si x = 0, 3 - 2y -y2 = 0 ⇔ y = 1 ó y = -3, por tanto, los puntos de corte con el eje de ordenadas son (0,1) y (0,-3)
Si y=0, entonces x=3, de manera que el punto de corte con el eje de abscisas es (3,0).
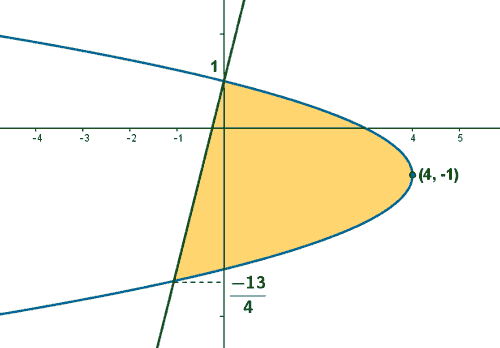
Teniendo en cuenta todo lo anterior el área del recinto es:

5) Determinar el área del recinto limitado por la parábola
y 2 = 2x
y la recta que une los puntos ( 2, -2 ) y ( 4, 2√2 )
Observamos que no es difícil esbozar la parábola que nos dan en el enunciado ya que pasa por el punto (0,0) en el cual alcanza un mínimo en x ya que x'=y, y además, x''=1>0.
Vemos ahora que los puntos del enunciado están sobre la parábola. En efecto,
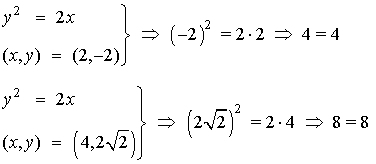
Calculamos ahora la ecuación de la recta:
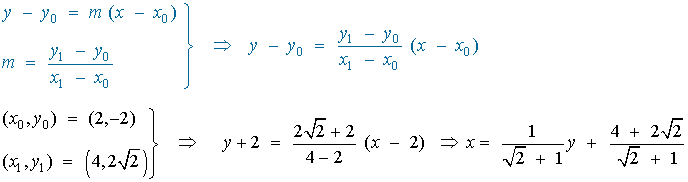
Teniendo esto en cuenta la gráfica de la recta y la parábola es la siguiente:
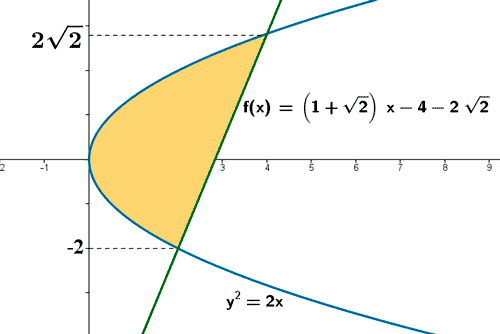
A la vista de la gráfica bastará con que integremos respecto a y entre -2 y 2√2:
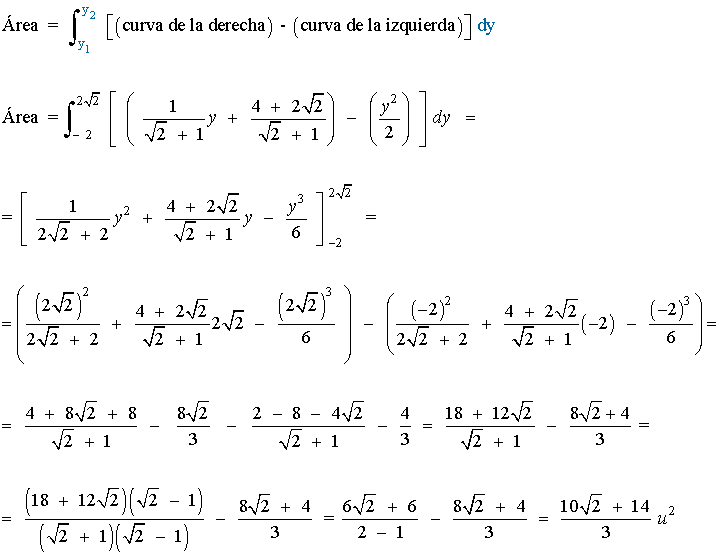
6) Hallar el área encerrada por
y2+ 2y + x - 3 = 0 e y = x + 1
Los puntos de corte de la parábola
x = -y2- 2y + 3
con los ejes son ( 0 , 1 ), ( 0 , -3 ) con el eje OY y ( 3 , 0) con el eje OX. Además la parábola alcanza un máximo de la x en el punto ( 4 , -1 ).
Puntos de intersección de la recta y la parábola
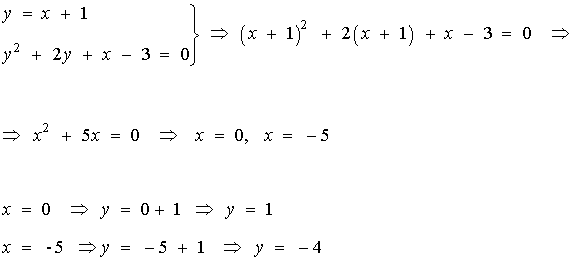
Y los puntos de intersección son ( 0 , 1 ) y ( -5, -4 ).
Teniendo en cuenta todo lo anterior podemos esbozar la gráfica como sigue:
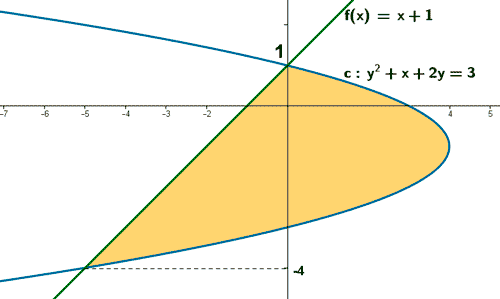
A la vista de la gráfica podemos calcular el área que nos piden integrando con respecto a y entre -4 y 1.
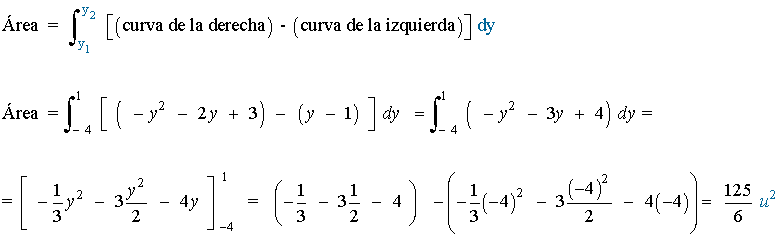
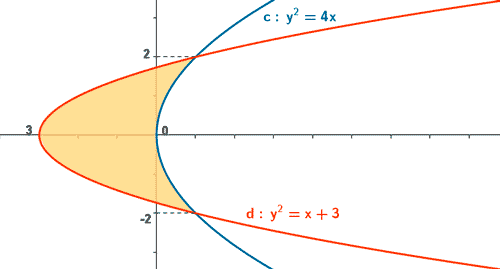
7) Hallar el área limitada por las curvas y2 = 4x ; y2 = x + 3.
Empezamos encontrando los puntos en los cuales se intersecan las dos curvas
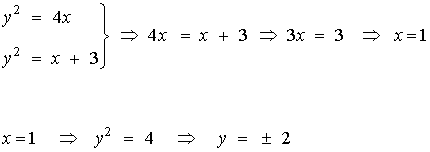
de manera que los puntos de intersección son ( 1, 2 ) y ( 1 , -2 ).

A la vista de la gráfica, el área pedida se calcula como sigue:



 INICIO
INICIO