Las funciones trigonométricas inversas
Para que una función tenga inversa, esta función tiene que ser inyectiva.
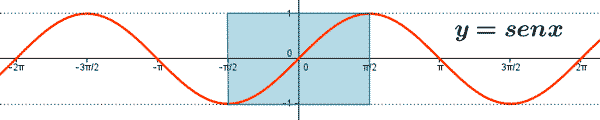
Las funciones trigonométricas no son inyectivas en todo su dominio, sólo en algunos intervalos, como se puede observar en la gráfica correspondiente.
f(x) = sen x es inyectiva en [-π/2, π/2] .
La función arcoseno
La función inversa de la función seno f(x) = sen x se denomina arcoseno y se representa por f-1(x) = arc sen x o f-1(x) = sen-1(x) . Esta función da el valor del ángulo conociendo el valor del seno.
![]()
El arcoseno de x es el ángulo cuyo seno es x .
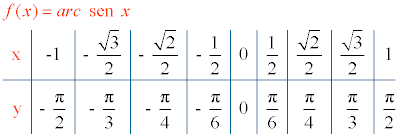
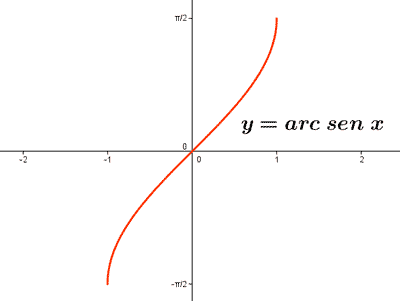
1) Su dominio es [-1, 1] .
2) Su recorrido es [-π/2, π/2] .
3) Puntos de corte:
La gráfica pasa por el punto (0, 0).
4) Es creciente en todo su dominio.
5) Es una función impar.
6) Máximo absoluto en (1, π/2) y mínimo absoluto en (-1, -π/2).
No confundir:
![]()
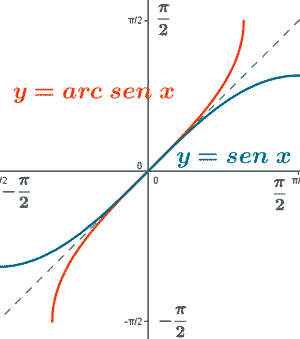
Representación gráfica de las funciones seno y arcoseno
La composición entre el seno y el arcocoseno es la identidad:
![]()
![]()
Ambas funciones son simétricas respecto a la recta y = x .
Hallar arc sen (√3/2)
Se busca un ángulo α en el intervalo [-π/2, π/2] para el cual:
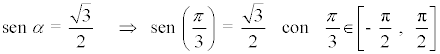
Por lo tanto, tenemos que:
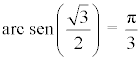

La función arcoseno es la función inversa de la función seno, luego en general se tiene que:
arc sen ( sen(x) ) = x
Por tanto:
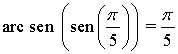


 INICIO
INICIO

